4.2. Расчет закрытой цилиндрической зубчатой передачи
Расчет зубчатой закрытой передачи производится в два этапа: первый расчет — проектный, второй — проверочный. Проектный выполняется по допускаемым контактным напряжениям с целью определения геометрических параметров редукторной пары. В процессе проектного расчета выбирают ряд табличных величин и коэффициентов; результаты некоторых расчетных величин округляют до целых или стандартных значений; в поиске оптимальных решений приходится неоднократно делать пересчеты. Поэтому после окончательного определения параметров зацепления выполняют проверочный расчет.
Проектный расчет
Исходные данные:
схема редуктора; Т1, Т2, Нм; n1, n2, мин‾¹;
uзп (табл.1.4.5); Тmах/Тnоm (табл. 7.1.1, с. 110);
[σ]Н, [σ]F, МПа (табл. 4.1.4);
[σ]Н mах 1(2), [σ]Fmах 1(2), МПа (табл. 4.1.1).
4.2.1. Определить главный параметр — межосевое расстояние аW, мм:
где: а) Ка — вспомогательный коэффициент. Для косозубых передач Ка = 43, для прямозубых — Ка = 49,5;
б) ψа = b2 /aW — коэффициент ширины венца колеса, равный 0,28…0,36 — для шестерни, расположенной симметрично относительно опор;
в) и = изп —передаточное число редуктора;
г) Т2 — вращающий момент на тихоходном валу, Нм;
д) [σ]Н — допускаемое контактное напряжение колеса с менее прочным зубом;
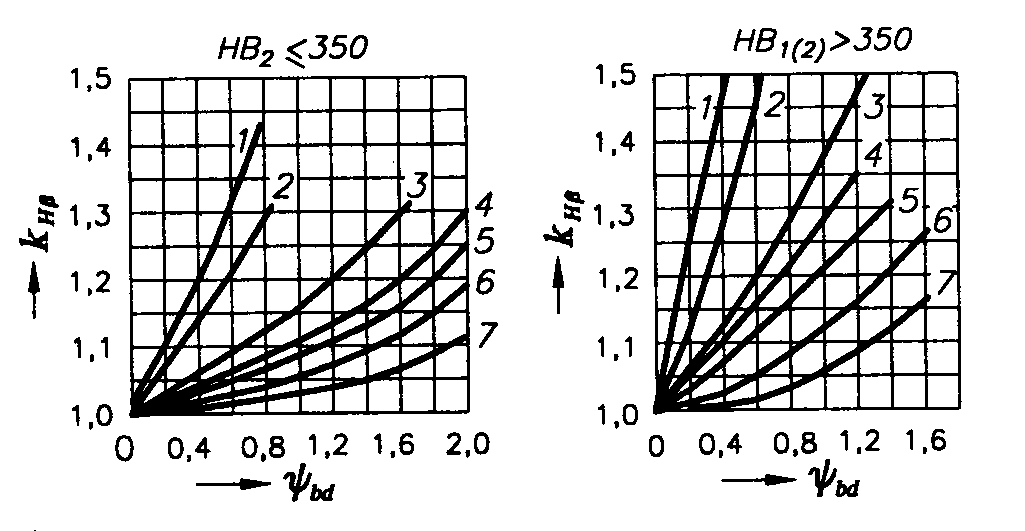
е) kНβ — коэффициент неравномерности распределения нагрузки по ширине венца, kНβ = f (НВ, расположения колес относительно опор, ψbd) (рис. 4.2.1а, б); ψbd — коэффициент ширины шестерни относительно ее диаметра, ψbd = b/d1 = f (НВ, расположения колес относительно опор) (табл. 4.2.1). Для прирабатывающихся зубьев kНβ =1;
ж) kА — коэффициент внешней динамической нагрузки (табл. 4.2.3).
Таблица 4.2.1
Рекомендуемые значения коэффициента ψbd = b/d1
Расположение колес относительно опор |
Твердость рабочих поверхностей зубьев |
|
НВ1(2) ≤ 350 |
НВ1(2) > 350 |
|
Симметричное Несимметричное Консольное |
0,8…1,4 0,6…1,2 0,3…0,4 |
0,4…0,9 0,3…0,6 0,2…0,25 |
|
|
а |
б |
|
|
в |
г |
|
|
д |
|
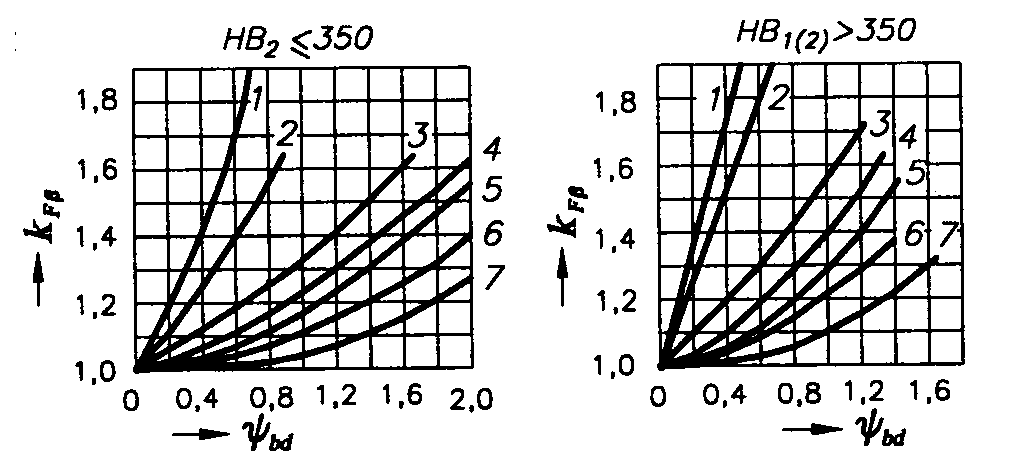
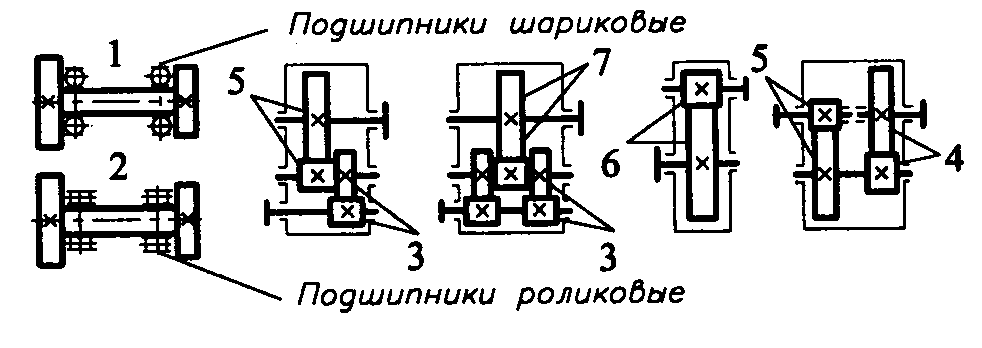
Рис. 4.2.1. Графики для определения коэффициентов
неравномерности распределения нагрузки по ширине венца:
а и б — при расчете контактной прочности зубьев kНβ; в и г — при расчете зубьев на изгиб kFβ; д — схемы редукторов
Полученное значение межосевого расстояния аW округлить до ближайшего значения в соответствии с ГОСТ (табл. 4.2.2).
Таблица 4.2.2
Значения межосевых расстояний аW
ГОСТ 2185—66
Ряд |
Межосевое расстояние аW, мм |
1 |
40; 50; 63; 80; 100; 125; 160; 200; 250; 315; 400; 500; 630… |
2 |
71; 90; 112; 140; 180; 224; 280; 355; 450; 560; 710; 900… |
Таблица 4.2.3