Рисунок 1

Метод Стокса

Мегде R - радиус тела, v - его скорость, а  - динамическая вязкость жидкости. На применении этой формулы основывается метод измерения динамической вязкости, называемый методом Стокса. При определении вязкости по методу Стокса измеряется скорость установившегося (равномерного) падения небольшого шарика в жидкости.

На шарик, жидкости, действуют три силы (см. рисунок 1) - сила тяжести P, направленная вниз, выталкивающая сила - сила Архимеда F_A, направленная вверх и сила сопротивления F_c, направленная против движения, т.е. тоже вверх.

Если опустить шарик в жидкость, то он вначале он будет двигаться ускоренно, т.к. P>F_A+F_c. сила падающий в вязкой сопротивления F_c будет расти согласно формуле Стокса до тех пор пока не наступит равновесие сил:

P=F_A+F_c (2)

С этого момента движение шарика будет равномерным. Из уравнения (2) и определяется коэффициент вязкости.

Силу тяжести находим по объему v и плотности _m металлического шарика:

(3)

Силу Архимеда определяем по объему шарика и плотности жидкости :

(4)

Подставляя в (2) выражения (1), (3), (4) получим:

(5)

Решение уравнения (5) относительно  дает расчетную формулу:

(6)

Учитывая, что R=d/2 и , формулу (6) целесообразно представить в виде

(7)

Методика определения вязкости жидкости, основанная на формуле Стокса, даёт правильные результаты лишь в том случае, если выполнены предположения, сделанные при выводе этой формулы. Одним из предположений является ламинарный характер обтекания шарика жидкостью. Характер обтекания определяется значением числа Рейнольдса

, (10)

Где D –характерный размер, в случае цилиндрической трубы следует брать ее диаметр. Обтекание является ламинарным лишь при не очень больших значениях числа Re(<20).

Сборка лабораторной установки, проведение эксперимента и обработка результатов изменений

1. 

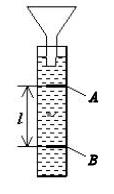
   Рисунок 2 Схема лабораторной установки

   Основной частью лабораторной установки является стеклянный цилиндр, заполненный техническим вазелином. С помощью воронки, укрепленной в верхней части цилиндра, в него опускается металлический шарик. Опущенный в жидкость шарик сначала падает ускоренно, а через некоторое время начинает падать равномерно. Расстояние между метками А и В на цилиндре, которое шарик проходит равномерно, измеряется линейкой.

2. Измерительные приборы, используемые в данной работе – линейка, отсчетный микроскоп и секундомер. Необходимо определить цену деления и приборную погрешность данных приборов, данные об измерительных приборах внести в таблицу 1

3. Используя отсчетный микроскоп, измерить диаметр шарика d. Для этого поместить шарик в смотровое окно микроскопа, установить резкое изображение шарика, а также шкалы отсчетного микроскопа с помощью винта.

4. Измерить время t прохождения шариком расстояния АВ, для этого опустить шарик через воронку в цилиндр и в момент прохождения уровня А включить секундомер, при прохождении через метку В выключить секундомер. Данные t и d записать в таблицу 2.

5. Повторить измерения п.п. 2 и 3 для 5 разных шариков, результаты занести в таблицу2.

таблица 1

Прибор	Предел измерений	Цена деления	Приборная погрешность
Линейка
Отсчетный микроскоп
Секундомер

таблица 2

№	d, см	t, с	i	 -i	( -i) 2	Расчетные формулы
						=0,9; (N)= ; сл=(N)S= ;

Обработка результатов измерений:

6. Рассчитайте по формуле (7) коэффициент вязкости для пяти проделанных измерений, результаты расчетов внесите в таблицу 2.

7. Рассчитайте абсолютную случайную погрешность измерения величины вязкости _сл=_(N)S, где _(N)-коэффициент Стьюдента, значения которого для заданных надежности  и числа проведенных измерений N взять из таблицы.

8. Используя технические данные приборов из таблицы 1, рассчитайте относительную приборную погрешность в измерении вязкости, взяв минимальные значения t и d:

9. Вычислите абсолютную приборную погрешность измерения коэффициента внутреннего трения:

10. Вычислите общую абсолютную погрешность измерения коэффициента внутреннего трения:

И запишите результат в виде:

11. По данным одного из измерений рассчитайте число Рейнольдса и сделайте заключение о характере течения, сопровождающего движение шарика, и о соотношении сил трения и давления, действующих на шарик.

Приложение 1 Бланки Лабораторных работ

Лабораторная работа № 1.

Определение скорости пули баллистическим методом .

Фамилия И.О.
Группа
№ бригады

Таблица 1 Характеристики приборов измерения:

Прибор	Предел измерений	Цена деления	Погрешность прибора
Линейка
Датчик угла поворота

Таблица 2 Измерение угла отклонения:

№	0i,	1i,	i=1i-0i,	∆ i ,	∆ i 2, 	Расчётные формулы
						N=5; ; =0,9; (N)= ; сл=(N)S= ; =(сл+пр)*/180=
			ср		∑∆i2

Таблица 3 Вычисление скорости пули

M, кг	m, кг	l , м	ср	v, м/c	v, м/c
0.034	0.0083

=

Вычисление ошибки определения скорости пули:

=

Лабораторная работа № 2.

Определение моментов инерции тел

Фамилия И.О.
Группа
№ бригады

таблица 1 Характеристики приборов измерения:

Прибор	Предел измерений	Цена деления	Погрешность прибора
Линейка
Штангенциркуль
Датчик угловой скорости

таблица 2 Исходные данные для проведения опытов:

радиус катушки муфты RR, м	масса груза m∆m, кг		удаление грузов от оси l ∆l, м
	0.02380.0001	0.04760.0001

таблица 3 Измерение углового ускорения:

R, м	l, м	m, кг	, радс-2			ср, радс-2	J, кгм2

Вычисление момента инерции маятника Обербека:

Таблица 4 Вычисление погрешности измерения углового ускорения

, радс-2			i2, радс-2	S	сл, радс-2	, радс-2

N=3 =0,9 _(N)

_сл=_(N)S _пр= =_сл+_пр

Лабораторная работа № 3.

ИЗУЧЕНИЕ ЗАКОНА СОХРАНЕНИЯ МОМЕНТА ИМПУЛЬСА

Фамилия И.О.
Группа
№ бригады

таблица 1 Характеристики приборов измерения:

Прибор	Предел измерений	Цена деления	Погрешность прибора
Линейка
Датчик угловой скорости

таблица 2 Данные о лабораторной установке

m1, кг	m2, кг	R, м	m, кг	R1, м	R2, м	H, м.
0.025	0.0045	0,012	0.0238	0.007	0.0015	0.02

таблица 3 Определение момента инерции стержней и муфты

m1, кг	m2, кг	R, м	l, м	Jм, кгм2	Jс, кгм2	Jо=Jм+2Jс,кгм2
0.025	0.0045	0,012

- момент инерции муфты

- момент инерции спицы

J_о=J_м+2J_с момент инерции стержней и муфты

таблица 4 Определение моментов инерции грузов при различном удалении от оси и момента импульса системы

№	r, м	r1 ,м	r2, м	1, с-1	2, с-1	J1 кгм2	J2,кгм2	L1,кгм2с-1	L2 кгм2с-1

момент инерции грузов до разлета

момент инерции грузов после разлета

L₁=(J₁+J_o) ₁ момент импульса системы в начальном состоянии

L₂=(J₂+J_o) ₂ момент импульса системы в конечном состоянии

Лабораторная работа № 4.

МАЯТНИК МАКСВЕЛЛА

Фамилия И.О.
Группа
№ бригады

таблица 1 Характеристики приборов измерения:

Прибор	Предел измерений	Цена деления	Погрешность прибора
линейка
секундомер

таблица 2 Данные о лабораторной установке

d0, мм	D, мм	m0, кг	mд, кг	m, кг
9±0.1	100±0.1	0.062±0.001	0.490±0.001	0.552±0.001

таблица 3 Время движения

№	ti,c	ti,c	ti2,c	Расчетные формулы
				N=5; ; =0,9; (N)= ; tсл=(N)S= t=tсл+tпр=
	t	ti2