МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ

Бронницкий филиал

«МОСКОВСКИЙ АВТОМОБИЛЬНО-ДОРОЖНЫЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ (МАДИ)»

МАДИ

Букерма л.Б.

ФИЗИКА

Часть 1. Механика

Методические указания

по выполнению лабораторных работ по физике

для студентов, обучающихся по специальности

190601 «Автомобили и автомобильное хозяйство»

Бронницы 2010

Бронницкий филиал

«МОСКОВСКИЙ АВТОМОБИЛЬНО-ДОРОЖНЫЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ (МАДИ)»

Кафедра МЕН

	«УТВЕРЖДАЮ» Заместитель директора Бронницкого филиала МАДИ (ГТУ) _ ___________________ С.Н.Пестова

Букерма л.б.

ФИЗИКА

Часть 1. Механика

Методические указания

по выполнению лабораторных работ по физике

для студентов, обучающихся по специальности

190601 «Автомобили и автомобильное хозяйство»

Бронницы 2010

Введение

Программа изучения курса физики в Бронницком филиале МАДИ предусматривает выполнение лабораторных работ в соответствии с темами курса. Лабораторные работы по механике открывают цикл лабораторных работ по физике и являются важной частью учебного процесса. Целью первого цикла лабораторных работ является определение физических величин, закрепление пройденного материала, знакомство с основными методами исследования и определения погрешностей. В ходе лабораторных работ студенты получают умения и навыки, которые они будут использовать как на протяжении изучения курса физики, так и во многих других дисциплинах – гидравлике, теории машин и механизмов, электротехнике и других. Основным средством для проведения лабораторных работ по механике является компьютерная измерительная система, которая включает в себя измерительные датчики, аналогово-цифровые преобразователей, а также необходимое программное обеспечение.

Перечень лабораторных работ

1. Измерение скорости тела методом баллистического маятника

2. Определение моментов инерции тел

3. Изучение закона сохранения момента импульса

4. Маятник Максвелла

5. Измерение вязкости жидкости методом Стокса компьютерным способом

6. Измерение вязкости жидкости методом Стокса

Лабораторная работа 1

ИЗМЕРЕНИЕ СКОРОСТИ ТЕЛА

МЕТОДОМ БАЛЛИСТИЧЕСКОГО МАЯТНИКА

Цель работы: измерение скорости шарика с помощью баллистического маятника.

Оборудование:
баллистический маятник метательное устройство металлический шарик штатив универсальный	датчик угла поворота измерительный блок L‑микро линейка

Баллистический маятник представляет собой массивное тело, закрепленное таким образом, что оно может совершать колебания. Тело, скорость которого хотят измерить, неупруго сталкивается с первоначально покоящимся маятником. После этого маятник отклоняется от положения равновесия и начинает совершать колебания. Измерив угол максимального отклонения баллистического маятника, можно определить скорость, с которой двигалось тело до столкновения с маятником.

1-штатив, 2-стенд, 3- баллистический маятник, 4- метательное устройство, 5 -спица

Рис 1 Устройство баллистического маятника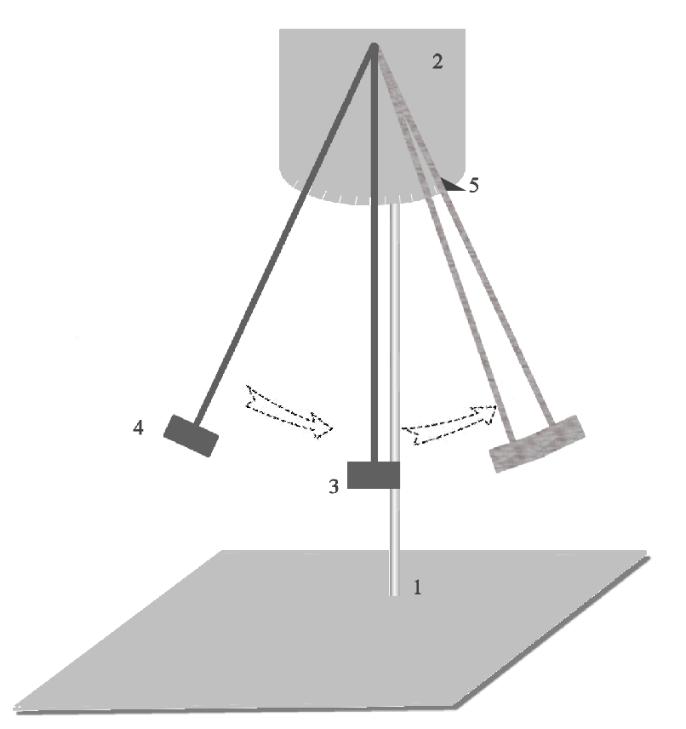

Применяемый в данной работе баллистический маятник устроен следующим образом (рисунок 1).

На штативе 1 укреплен стенд 2 с нанесенной на него шкалой угла поворота баллистического маятника. На стенд соосно крепятся два цилиндра переменной массы на тонких спицах, один из которых (3) служит баллистическим маятником, а другой (4) является метательным устройством, сообщающим баллистическому маятнику импульс. Тонкая подвижная спица 5 позволяет фиксировать угол поворота баллистического маятника.

Рассмотрим взаимодействие цилиндров.

В момент времени t₁ (рисунок 2а) первый цилиндр подлетает к первому со скоростью v, второй цилиндр при этом неподвижен. В момент времени t₂ (рисунок 2б) цилиндры слипаются и начинают движение вместе со скоростью u, при этом часть кинетической энергии первого цилиндра израсходовалась на преодоление сил трения. В момент времени t₃ (рисунок 2в) маятник отклонился на угол , центр тяжести его поднялся на высоту h, а кинетическая энергия, полученная в результате удара, перешла в потенциальную.

В боковую поверхность цилиндра (1) массой M ввинчена тонкая спица (2), массой которой можно пренебречь по сравнению с массой цилиндра. Другой конец спицы закреплен в муфте (3) датчика угла поворота (4). Датчик угла поворота укреплен на вертикальной стойке штатива (5). Цилиндр 1 снабжен пластмассовой вставкой (6) для улавливания шарика, налетающего вдоль оси цилиндра. Вставка (6) выполнена в виде конуса с малым углом так, чтобы шарик (7) застревал в цилиндре примерно в его центре масс. Шарик выстреливается пружинным метательным устройством (8).

а б в

Рис 2 Взаимодействие шарика с маятником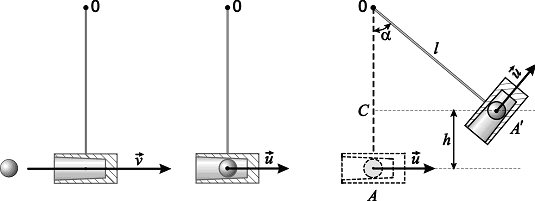

Рассмотрим взаимодействие шарика с маятником. В момент времени t₁ (рисунок 2а) шарик подлетает к цилиндру (1) со скоростью v, маятник при этом неподвижен. В момент времени t₂ (рисунок 2б) шарик уже застрял внутри баллистического маятника, часть кинетической энергии шарика израсходовалась на преодоление сил трения, часть передана баллистическому маятнику, в результате чего он приобретает скорость u. В момент времени t₃ (рисунок 2в) маятник отклонился на угол , центр тяжести его поднялся на высоту h, а кинетическая энергия, полученная в результате удара, перешла в потенциальную.

Столкновение шарика с маятником происходит не мгновенно, а в течение интервала времени t₁=t₂-t₁. Во время столкновения t₁ система не является консервативной, т.к. совершается работа против силы трения, но она является замкнутой, точнее, по оси удара действуют только внутренние силы и, следовательно, выполняется закон сохранения проекции импульса на направление движения шарика. Этим законом можно воспользоваться и записать

(1)

Здесь mv - импульс шарика до удара, (M+m)u - импульс маятника с застрявшим в цилиндре шариком после удара. (m - масса шарика, М - масса баллистического маятника). Масса спицы мала по сравнению с массой цилиндра, ей можно пренебречь. Из равенства (1) определим скорость маятника в момент времени непосредственно после завершения процесса столкновения:

(2)

интервал времени столкновения t₁ во много раз меньше времени t₂=t₃-t₂ качания маятника (t₁<<t₂), поэтому за время столкновения шарик уже остановится относительно цилиндра, сообщив последнему начальную скорость u, а цилиндр еще не успеет сдвинуться на заметную величину. Таким образом, две части процесса превращения энергии происходят последовательно друг за другом, и рассматривать их можно раздельно.

Если в первой части процесса система замкнута, но не консервативна, то во второй части, во время качания, система незамкнута, но консервативна. Действительно, на баллистический маятник с застрявшим в нем шариком действуют сила тяжести (M+m)g и сила упругости спицы - внешние силы по отношению к системе шарик - маятник. Следовательно, система незамкнута, и закон сохранения импульса неприменим. Но сила тяжести консервативна, сила упругой реакции спицы тоже консервативна, значит система шарик - цилиндр является консервативной. Отметим, что есть еще третья сила - сила трения в датчике угла поворота, но эта сила мала и ею можно пренебречь по сравнению с консервативными силами.

В консервативной системе соблюдается закон сохранения энергии, это значит, что кинетическая энергия, которую приобретает маятник в момент времени t₂ перейдет в потенциальную энергию поднятой на высоту h массы (M+m) цилиндра с шариком внутри. Кинетическая энергия T в начале движения записывается так:

(3)

Подставив (2) в (3) и проведя некоторые преобразования, получим:

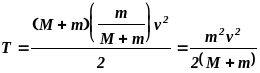(4)

Потенциальная энергия U поднятого нa высоту h маятника равна:

(5)

и на основе закона сохранения энергии можно записать:

(6)

Решая уравнение (6) относительно v, получаем:

(7)

Высота поднятия центра масс маятника при известном расстоянии l от точки подвеса до центра масс маятника определяется по углу отклонения  маятника, который измеряется датчиком угла поворота.

На рис. 2в схематически показано поднятие центра масс маятника на высоту h в результате его отклонения на угол . Из прямоугольного треугольника OA^'C следует, что OC=lcos. h=AO-OC=l- lcos, или:

(8)

Подставляя (8) в (7), получим расчетную формулу для определения скорости шарика:

(9)

Учитывая, что , получим расчетную формулу для определения скорости шарика:

(10)

Сборка лабораторной установки, проведение эксперимента и обработка результатов измерений

1. Соберите установку как показано на рисунке 1. Штатив собирается с длинной вертикальной стойкой (5), в верхней части которой закрепляется датчик угла поворота (4) с муфтой (3). Ось вращения датчика должна быть горизонтальной. В муфту вверните до упора длинную спицу (2), на конце которой закрепите цилиндр баллистического маятника (1). Ось цилиндра должна располагаться в плоскости колебаний маятника. Это направление фиксируется с помощью контргайки (9).

Рисунок 3 Схема подключения лабораторной установки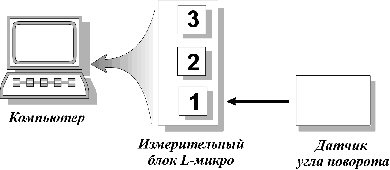

Измерьте расстояние от оси цилиндра баллистического маятника до оси вращения датчика угла поворота. Полученную величину запишите в таблицу 2.

2. подключите измерительный блок L-микро к разъему последовательного порта компьютера. После этого подсоедините его к сети (220 В, 50 Гц) и включите. Разъем датчика угла поворота присоедините к первому каналу измерительного блока (рис. 3).

3. Запустите программу L^‑phys.exe, выберите пункт меню «Список работ» и в появившемся на экране списке выберите лабораторную работу «Измерение скорости тела методом баллистического маятника».

4. Датчик угла поворота регистрирует углы в интервале 0 - 3600 , т. е. делает 10 оборотов вокруг своей оси, однако наибольшая точность измерений достигается в диапазоне 0-360. Для того, чтобы угол отклонения маятника при измерениях не выходил за рамки указанного интервала, его положение равновесия должно быть в диапазоне углов 90-270. Выберите пункт меню «Настройка». Цифра на экране будет соответствовать текущему значению угла, регистрируемого датчиком. Установите требуемое значение угла положения равновесия, аккуратно вращая маятник вокруг оси датчика и при необходимости, сняв датчик со штатива и повернув его корпус на 180.

5. Зарядите метательное устройство. Утопите шток, толкающий шарик, внутрь цилиндрической части корпуса. При этом Вы сожмете пружину, которая находится внутри корпуса. После этого вложите шарик в желоб так, чтобы он касался конца штока.

Выберите в меню на экране компьютера пункт «ЗАПУСК». Заряженное метательное устройство расположите вплотную к цилиндру баллистического маятника. Обратите внимание на то, что ось симметрии метательного устройства, определяющая направление скорости движения шарика, во-первых, должна быть горизонтальной и, во-вторых, находиться в плоскости колебаний баллистического маятника. Только при соблюдении указанных условий удар будет прямым и центральным, т. е. будут справедливы соотношения, использованные выше при выводе расчетной формулы..

Произведите выстрел (нажмите кнопку на корпусе метательного устройства) и уберите метательное устройство, чтобы маятник мог беспрепятственно двигаться после возврата в положение равновесия.

3. После прекращения записи данных на экране компьютера возникает график зависимости угла отклонения от времени. Вам необходимо определить угол максимального отклонения. Для этого, используя клавиши , следует подвести курсор (вертикальную черту на экране) к интересующей Вас точке графика и выписать из квадрата на экране численное значение угла, которое высвечивается в верхней части экрана.

Нулевой угол отклонения маятника (положение равновесия) соответствует произвольному значению угла в диапазоне 90270. Поэтому при обработке данных для определения максимального угла отклонения необходимо из значения угла, полученного для первого максимума или минимума кривой на экране, вычесть значение угла, соответствующего положению равновесия (прямая линия на экране, предшествующая движению маятника). Знак угла отклонения при этом, естественно, не имеет физического смысла и может быть опущен.

Чтобы убедиться в том, что потери на трение малы, следует также выписать в таблицу амплитуду второго колебания маятника и вычислить величину отклонения в противоположную сторону.

7. Эксперимент и предварительную обработку данных, описанные в п. 5, 6 следует повторить 5 раз и заполнить таблицу 1:

Таблица 1

	0 , град	1 , град	2 , град	=1-0 , град.	=2-0 , град.

Обозначения, принятые в таблице:

_{0 -} угол, измеряемый датчиком и соответствующий положению равновесия;

_{1 -} угол, измеряемый датчиком и соответствующие первому отклонению маятника;

_{2 -} угол, измеряемый датчиком и соответствующие второму отклонению маятника;

 и  - истинные величины углов отклонения.

7. Рассчитайте среднее значение угла отклонения (_ср) и на основании расчетной формулы определите скорость полета шарика (таблица 2). Необходимые для расчета значения массы маятника и шарика приведены в таблице 2.

8. Рассчитайте относительную погрешность измерения скорости шарика:

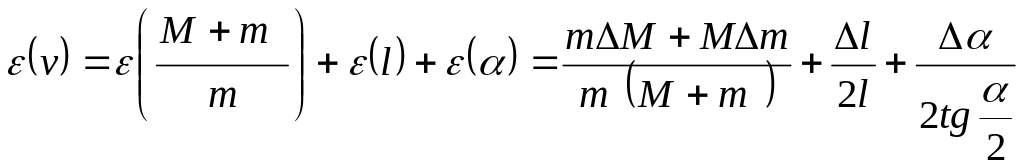
и абсолютную погрешность измерения:

Сделайте вывод о том, достаточно ли малы потери энергии при движении маятника.

Таблица 2

M, кг	m, кг	l , м	ср	v, м/c	v, м/c
0.034	0.0083

Обозначения, принятые в таблице:

M - масса баллистического маятника (цилиндра);

m - масса шарика;

l - расстояние от оси цилиндра до оси датчика вращения;

_ср - среднее значение угла отклонения;

v - скорость полета шарика;

v - погрешность определения скорости.

9. Подумайте, в чем физические причины некоторого разброса углов отклонения, наблюдаемого в эксперименте.

Указания по технике безопасности

0. Включать в сеть измерительный блок L-микро можно только после его подключения к разъему последовательного порта компьютера.

1. Следите за тем, чтобы углы отклонения маятника не выходили за рамки рабочего диапазона датчика угла поворота.

Лабораторная работа 2

ОПРЕДЕЛЕНИЕ МОМЕНТОВ ИНЕРЦИИ ТЕЛ

Цель работы: измерение момента инерции твердых тел, исследование зависимости момента инерции от конфигурации тела.

Оборудование:
штатив универсальный датчик угловой скорости с муфтой стержни (спицы) с перемещающимися по ним грузами - 4 шт. грузы ‑ 2 шт.	концентратор штангенциркуль линейка проволочка для подвешивания грузов

Момент инерции твердого тела можно определить с помощью вычислений. В тех случаях, когда тело неоднородно по своему составу или имеет сложную геометрическую конфигурацию, определение момента инерции производится экспериментально.

1-стержни, 2-муфта,3-груыз, 4-нить,6-груз, 7-датчик угловой скорости

Рисунок 1 Устройство маятника Обербека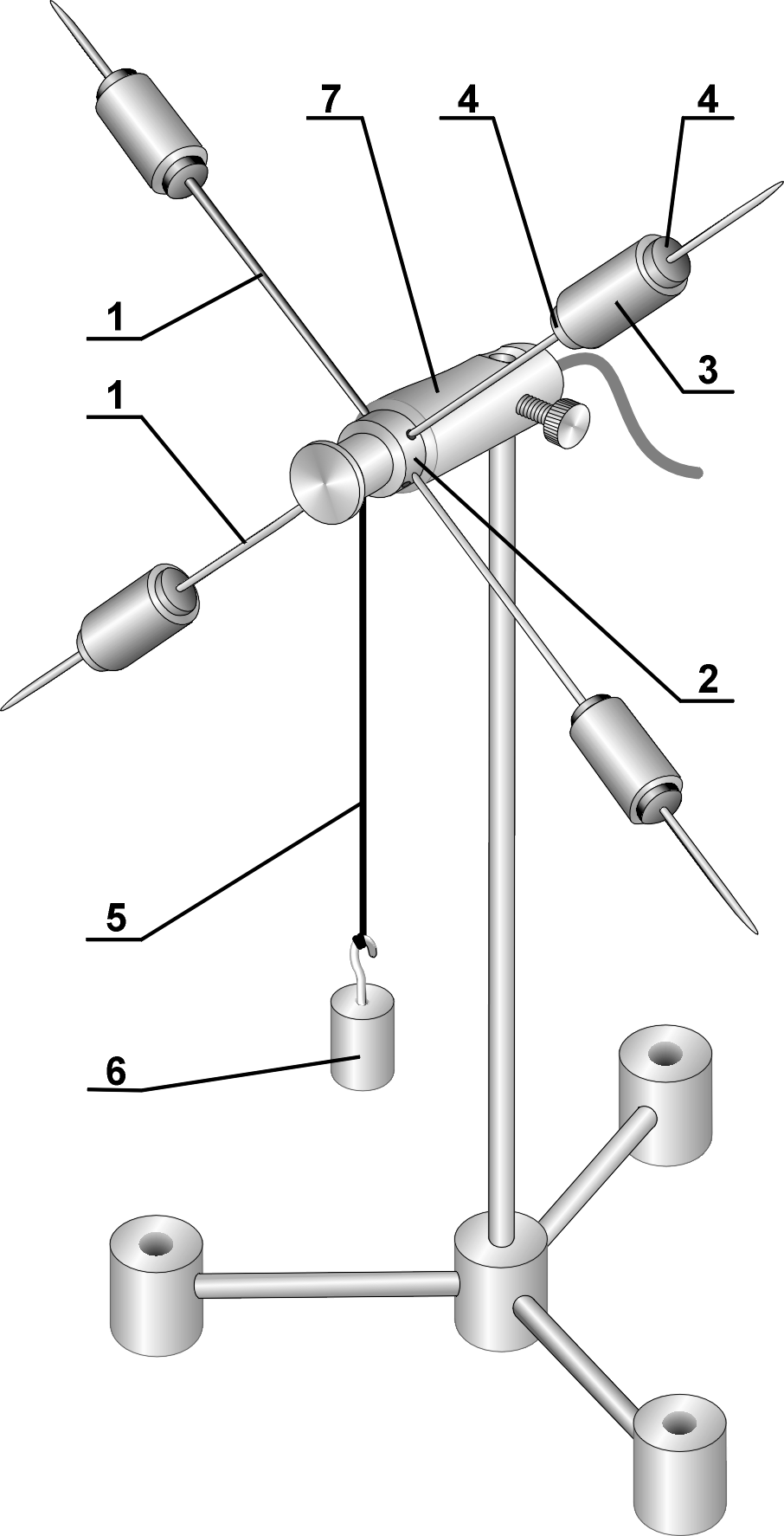

Экспериментальная установка, используемая в данной работе, исторически получила название "Маятник Обербека". Схема ее изображена на рисунке 1.

Маятник Обербека представляет собой четыре стержня (1), закрепленные в муфте (2). Ось вращения муфты расположена горизонтально. На каждом из стержней имеется груз (3), который с помощью специальных фиксаторов (4) может размещается на любом расстоянии от оси муфты. Таким образом момент инерции конструкции может изменяться в широких пределах. Раскрутка маятника Обербека осуществляется с помощью нити (5), предварительно намотанной на цилиндрическую поверхность муфты. К нижнему концу нити прикрепляются грузы (6) различной массы. Для проведения измерений муфта маятника Обербека надета на ось датчика угловой скорости (7), что позволяет записывать значения скорости вращения во время движения.

При выполнении лабораторной работы Вам необходимо измерить момент инерции маятника Обербека в двух случаях: при минимальном и максимальном удалении грузов от оси вращения. В каждом случае раскрутка маятника проводится двумя различными грузами. В соответствии с теорией изложенной ниже, это позволит при обработке данных исключить влияние сил трения.

Рассмотрим движение маятника Обербека на основе законов динамики. Груз на нити движется поступательно под действием силы тяжести и силы натяжения нити. При этом можно записать уравнение второго закона Ньютона для груза массой m:

ma=mg-T (1)

Отсюда находим силу натяжения нити T:

T=m(g-a) (2)

Эта сила, приложенная по касательной к окружности муфты, создает вращающий момент M=T^R (R - радиус цилиндрической поверхности муфты, на которую намотана нить).

Теперь, используя основной закон динамики вращательного движения, проанализируем вращение маятника Обербека. При этом следует учитывать момент M_Tp, создаваемый силами трения и тормозящий вращение. Определение этого момента затруднительно, т.к. его создают неизвестные по величине силы с известными относительно оси плечами. Ими могут быть силы сопротивления движению грузов со стороны воздуха или трения в оси датчика угловой скорости.

J=M-M_Tp=TR-M_Tp (3)

или

(4)

Угловое ускорение маятника  и линейное ускорение a груза на нити связаны формулой:

, (5)

Поскольку в экспериментах измеряется угловая скорость вращения и на ее основе определяется угловое ускорение маятника Обербека, то из (4) с помощью (5) следует исключить a:

(6)

Для того чтобы исключить из уравнения неизвестный момент трения M_Tp, можно провести эксперимент дважды с различными грузами m₁ и m₂. При этом угловые ускорения ₁ и ₂ и вращающие моменты M₁ и M₂ сил T₁ и T₂ окажутся различными. Запишем уравнения основного закона вращательного движения в первом и втором экспериментах:

(7)

Или, на основе (6):

(8)

Таким образом, (8) представляет систему двух алгебраических уравнений с двумя неизвестными - искомым моментом инерции J и моментом трения M_Tp. Исключив момент трения, найдем момент инерции J установки Для этого в системе (18) вычитаем второе уравнение из первого и получаем одно уравнение с искомым J:

(9)

Отсюда находим расчетную формулу для J:

(10)

Сборка лабораторной установки, проведение эксперимента и обработка результатов измерений.

1. Соберите установку как показано на рисунке 1. Штатив собирается с длинной вертикальной стойкой (8), на которой закрепляется датчик угловой скорости (7) с муфтой (2). Ось вращения датчика должна быть горизонтальной. В отверстия муфты необходимо ввернуть четыре одинаковых спицы (1), на которых располагаются подвижные грузы (3).

Установите грузы на стержнях в непосредственной близости от муфты и отрегулируйте положение грузов так, чтобы крестовина маятника (вал и стержни с грузами) находились в положении безразличного равновесия, т. е. оставались неподвижными в отсутствие внешнего воздействия в любом положении. Для этого нужно маятник отпустить и после остановки его движения передвинуть нижний груз ближе к оси маятника. Затем повернуть маятник и опять отпустить. Эти действия необходимо повторять до тех пор, пока после отпускания маятник не останется неподвижным.

Измерьте удаление грузов от оси и внесите полученное значение в таблицу (столбец «l, м»).

Закрепите один конец нити длиной 25 - 30 см на катушке муфты датчика угловой скорости и прикрепите к другому ее концу один из грузов. Перед запуском маятника Вам будет необходимо намотать нить на катушку муфты и таким образом поднять груз над поверхностью стола.

Измерьте с помощью штангенциркуля диаметр катушки муфты, определите значение ее радиуса R и внесите его в таблицу.

2. 

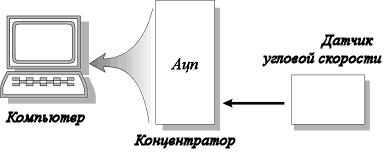
   Рис 2 Схема подключения лабораторной установки

   Подключите датчик угловой скорости к входу концентратора, присоединив последний к USB- входу компьютера.

3. После включения компьютера запустите программу физического практикума «Датчики» На панели устройств выберите соответствующий сценарий проведения эксперимента (Alt+C)

4. Запустите измерения для выбранного датчика (Ctrl+S) и сразу непосредственно вслед за запуском приведите в движение маятник, предоставив ему возможность вращаться под действием груза.

5. После вращения маятника на несколько оборотов остановите измерения (Ctrl+T)

6. Проведите обработку полученных данных в соответствии со сценарием и произведите оценку углового ускорения маятника по углу наклона графика зависимости угловой скорости от времени.

7. Действия, описанные в п.п. 4-6 необходимо повторить три раза для получения в дальнейшем усредненного значения углового ускорения при данных условиях эксперимента. Данные вносятся в столбец таблицы «, радс^-2», в клетки расположенные горизонтально.

8. Увеличить массу груза (добавить второй груз) и, выполнив п.п. 4-6, получить значения ускорения маятника Обербека.

9. Увеличить момент инерции маятника Обербека до значения, близкого к максимальному (раздвинуть грузы) и сбалансировать маятник (добиться безразличного равновесия на оси вращения). Оставить на нити только один груз. Записать в таблицу расстояние от центра грузов до оси (l) и выполнить измерения по пунктам 4-6.

10. При обработке данных следует:

а) рассчитать среднее значение углового ускорения _ср в каждой серии запусков и внести полученные результаты в таблицу.

б) на основании расчетной формулы, выведенной в теоретической части работы, определить значения моментов инерции J маятника Обербека при различных удалениях грузов от оси вращения. Массы грузов, с помощью которых раскручивается маятник Обербека, приведены в таблице.

в) вычислить погрешность измерения углового ускорения. По этим данным оценить погрешность измерения момента инерции маятника Обербека.

Таблица

R, м	l, м	m, кг	, радс-2			ср, радс-2	J, кгм2
		0.0238
		0.0476
		0.0238
		0.0476

Указания по технике безопасности

Следите за тем, чтобы грузы на стержнях маятника были надежно закреплены.

Лабораторная работа 3

ИЗУЧЕНИЕ ЗАКОНА СОХРАНЕНИЯ МОМЕНТА ИМПУЛЬСА

Цель работы: изучение динамики вращательного движения и закона сохранения момента импульса на примере системе с изменяющимся моментом.

Оборудование:
штатив универсальный датчик угловой скорости с муфтой стержни (спицы длинные) - 2 шт. грузы - 2шт.	ограничители хода грузов - 2 шт. устройство для раскрутки системы линейка концентратор.

Момент импульса при вращении относительно неподвижной оси равен произведению момента инерции J на угловую скорость . Закон сохранения момента импульса записываться в виде:

, (2)

Рисунок 1 Система с переменным моментом инерции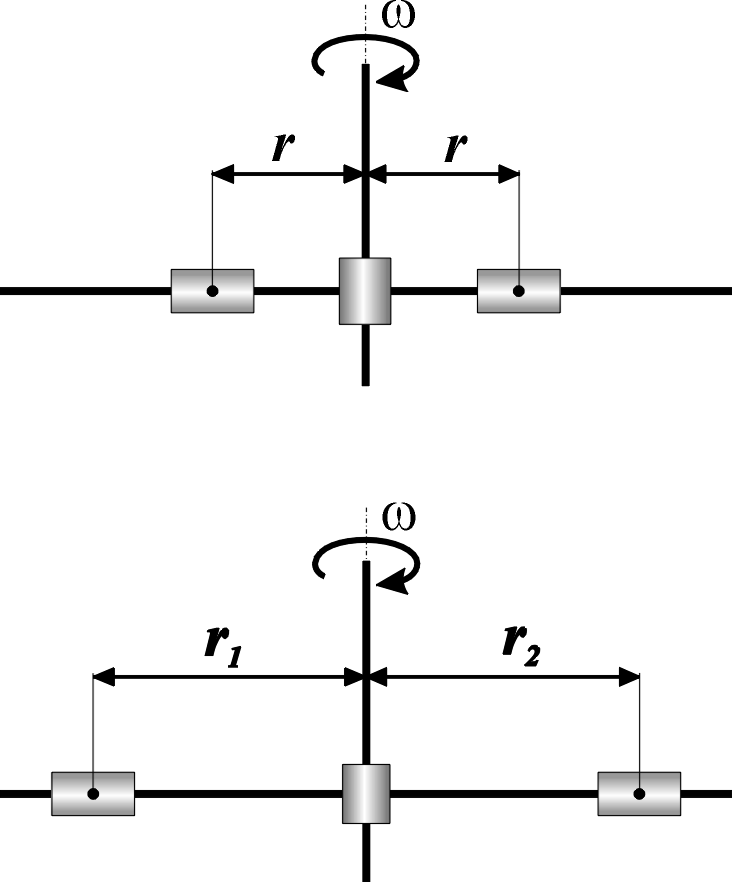

т.е. произведение момента инерции относительно неподвижной оси на угловую скорость относительно этой оси есть величина постоянная для механических систем, на которые не действуют моменты внешних сил или в которых главный момент внешних сил относительно оси вращения равен нулю. Экспериментальной проверке этого соотношения и посвящена данная лабораторная работа.

Механическая система с переменным моментом инерции схематически показана на рисунке1. Длинный тонкий стержень может вращаться в горизонтальной плоскости, вокруг оси, проходящей через его центр. На стержне имеется два груза, которые свободно скользят по нему. С помощью специального приспособления стержень приводится во вращение при минимальном удалении грузов от оси. После освобождения грузов они скользят по стержню до установленных заранее упоров. Момент инерции системы при этом возрастает, а вращение замедляется. Угловая скорость системы контролируется компьютерной измерительной системой. Измерение геометрических характеристик дает возможность определить начальное и конечное значения момента инерции. Таким образом, можно рассчитать моменты импульса в начальном состоянии (при максимальной скорости вращения) и в конечном состоянии (после разлета грузов) и сравнить их.

Сборка лабораторной установки, порядок проведения измерений и обработка результатов

1. Соберите экспериментальную установку как показано на рисунке2. Для этого возьмите штатив с короткой вертикальной стойкой (1) и установите на него датчик угловой скорости (2). В муфту, установленную на оси датчика (3), вверните два тонких стержня (4) и наденьте на них грузы (5). Для ограничения перемещения грузов по стержням на них устанавливаются резиновые шайбы (7, 8). раскрутка грузов производится специальной рукояткой (9), которая одновременно фиксирует начальное положение грузов. Устройство для раскрутки надевается на муфту датчика угловой скорости.

1-штатив, 2- него датчик угловой скорости, 3-муфта, 4-два тонких стержня,5-грузы ,6-ограничители, 7-специальная рукоятка

Рис 2 Схема лабораторной установки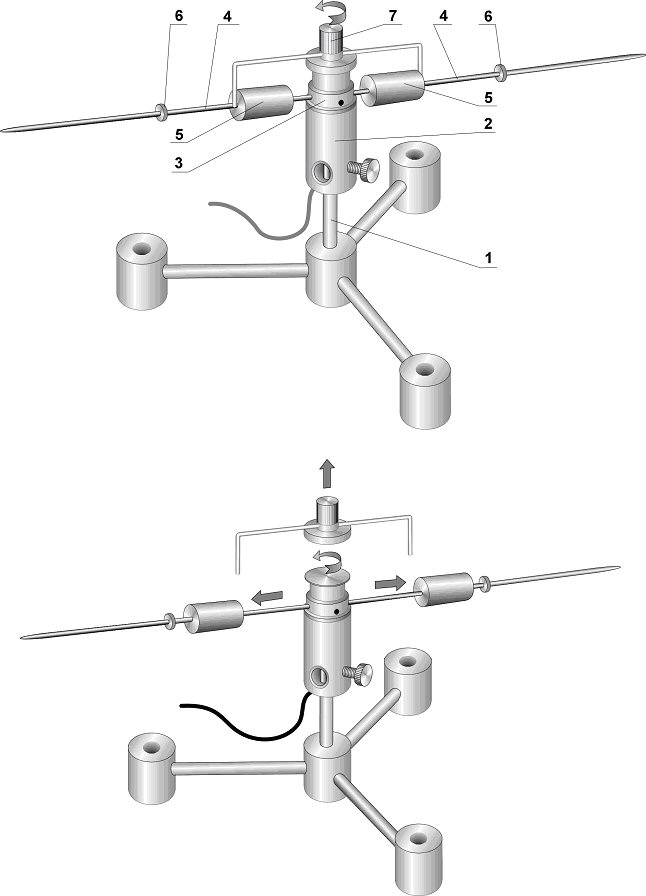

2. Подключите датчик угловой скорости к входу концентратора, присоединив последний к USB- входу компьютера

3. После включения компьютера запустите программу физического практикума «Датчики» На панели устройств выберите соответствующий сценарий проведения эксперимента (Alt+C)

4. Приступите к выполнению опыта. Для этого необходимо:

а) зафиксировать положение грузов с помощью устройства для раскрутки, установленного на муфту датчика. С помощью линейки измерить расстояние r от оси вращения до центров масс грузов и внести его в таблицу 2.

б) установить резиновые шайбы на определенном расстоянии от центра вращения системы.

в) включить режим регистрации данных компьютером. Для этого выбрать пункт меню «ЗАПУСК» (Ctrl+S) После вращения системы на несколько оборотов остановите измерения (Ctrl+T)

г) раскрутить систему грузов с помощью специального устройства и резко поднять его вверх, чтобы позволить грузам сдвинуться до резиновых шайб, ограничивающих их движение по стержням

Рисунок 3 Схема подключения лабораторной установки

д) После завершения записи данных на экране возникнет график зависимости угловой скорости вращения системы от времени. Вам следует определить начальное (₁) и конечное (₂) значения угловой скорости. Для этого с помощью мыши подведите курсор (вертикальную черту) к соответствующим точкам графика и выпишите значение угловой скорости из квадрата в верхней части экрана.

Отметим, что начальной скоростью вращения системы следует считать максимальное значение угловой скорости. Участок возрастания угловой скорости на графике соответствует раскрутке системы, а участок, где угловая скорость убывает ‑ разлету грузов, т. е. движению в отсутствие внешних сил. (Моментом силы трения пренебрегаем.)

е) с помощью линейки измерить и внести в таблицу 2 координаты центров масс грузов после разлета (r₁, r₂). Грузы могут не дойти до упоров или отойти от них после удара, т.е. оказаться на разных расстояниях от оси вращения.

5. Измерения необходимо провести при различных конечных положениях грузов, каждый раз проводя 2-3 запуска системы.

6. Обработка результатов эксперимента производится следующим образом:

а) момент инерции стержней и муфты, находящейся на оси датчика угловой скорости, сопоставим по величине с моментом инерции подвижных грузов, поэтому его необходимо учитывать при обработке данных эксперимента. Расчет момента инерции подвижной части установки (без грузов) выполняется в таблице 1.

Таблица 1.

m1, кг	m2, кг	R, м	l, м	Jм, кгм2	Jс, кгм2	Jо=Jм+2Jс,кгм2
0.025	0.0045	0,012

Обозначения, принятые в таблице:

m₁ - масса муфты на оси датчика угловой скорости;

m₂ - масса спицы;

R - радиус муфты;

l - длина спицы (от внешнего края муфты);

- момент инерции муфты;

- момент инерции спицы - находится с помощью теоремы Штейнера:

,

где - расстояние от центра масс спицы до центра вращения, - момент инерции тонкого стержня при вращении относительно оси, проходящей через его центр инерции.

б) С помощью таблицы 2 рассчитайте моменты инерции грузов при различном удалении от оси и моменты импульса системы в начальном и конечном состояниях.

таблица 2.

№	m, кг	r,м	r1,м	r2,м	1,с-1	2,с-1	J1,кгм2	J2,кгм2	L1=(J1+Jo) 1, кгм2с-1	L2=(J2+Jo) 2 , кгм2с-1
	0.0238

Обозначения, принятые в таблице:

m - масса груза;

r - радиус центров масс грузов до разлета;

r₁ - радиус центров масс одного из грузов после разлета;

r₂ - радиус центров масс другого груза после разлета;

₁ - угловая скорость системы до разлета грузов;

₂ - угловая скорость системы после разлета грузов.

Моменты инерции грузов в начальном и конечном состояниях рассчитываются следующим образом. Момент инерции цилиндрического груза при вращении относительно оси, проходящей через его центр инерции и перпендикулярной оси симметрии цилиндра, равен:

,

где R₁ -внешний радиус цилиндра, R₂ -радиус отверстия в цилиндре, H -длина цилиндрического груза. В работе используются грузы со следующими размерами: R₁ =0.007 м, R₂ =0.0015м, H =0.02 м.

Согласно теореме Штейнера моменты инерции грузов до разлета J₁ и после разлета J₂ равны:

;

.

L₁=(J₁+J_o) ₁ - момент импульса системы до разлета грузов;

L₂=(J₂+J_o) ₂ - момент импульса системы после разлета грузов.

в) Сопоставьте значения моментов импульса до и после разлета грузов и проанализируйте причины, которые приводят к некоторым отличиям в полученных результатах.

Указания по технике безопасности

Перед раскруткой системы убедитесь в правильной установке ограничителей хода грузов.

Лабораторная работа 4

МАЯТНИК МАКСВЕЛЛА

Цель работы: измерение момента инерции осесимметричного твердого тела в виде диска и сравнение с расчетными значениями.

Оборудование:
штатив универсальный маятник Максвелла электромагнит оптодатчик	измерительный блок L-микро блок питания линейка.

Рисунок 1 Силы, действующие на Маятник Максвелла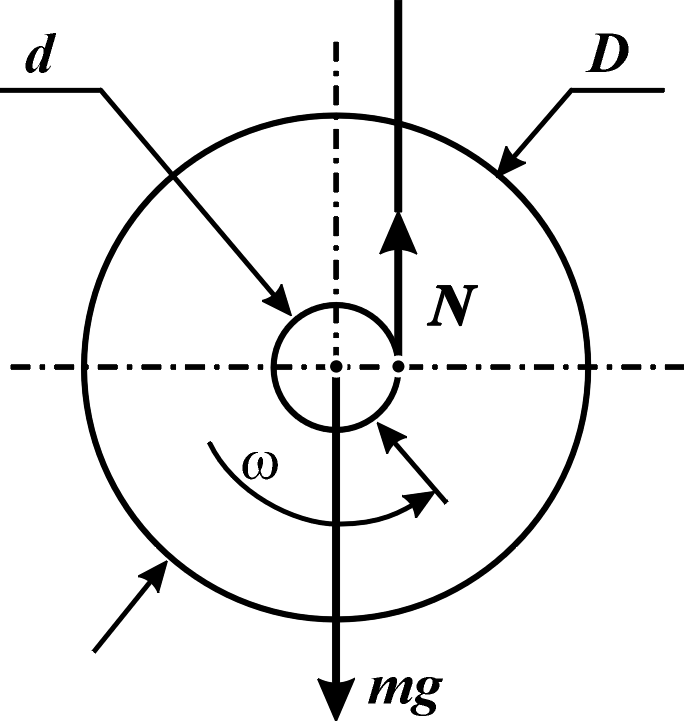

Маятник Максвелла представляет собой диск, неподвижно установленный на оси. На концах оси симметрично относительно диска закрепляются нити, с помощью которых маятник подвешивается к штативу. При вращении оси нити могут наматываться на ось или разматываться, обеспечивая тем самым перемещение маятника вверх и вниз. Если, намотав нити на ось, поднять маятник на некоторую высоту и отпустить его, то он начнет совершать колебательное движение в поле силы тяжести. В нижней точке маятник приобретает наибольшую скорость вращения, и, продолжая вращаться по инерции, снова поднимается на некоторую высоту за счет наматывания нитей на ось. После достижения верхней точки, где скорость вращения маятника становится равной нулю, он начинает падать, вращаясь при этом в другую сторону. На рис.1 показана схема сил, действующих на вал. Движение маятника осуществляется под действием силы тяжести и силы натяжения нитей . Движение маятника является равноускоренным до тех пор, пока нити хотя бы частично намотаны на вал. При этом угловая скорость  вращения диска вокруг оси, и линейная скорость v геометрической оси диска связаны между собой соотношением:

, (1)

где d - диаметр вала. Иными словами, скорость движения центра масс маятника равна скорости сматывания нитей с вала.

Кинетическая энергия диска равна

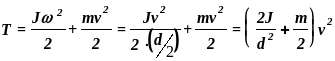, (2)

где J -момент инерции маятника.

В соответствии с законом сохранения энергии при движении в поле силы тяжести кинетическая энергия маятника, который опустился с высоты h, равна его потенциальной энергии на этой высоте, поэтому можно записать:

(3)

При равноускоренном движении скорость v выражается через высоту падения h и время движения t на основании кинематических соотношений:

и (4)

где a - ускорение, с которым движется центр масс диска. Из формул (4) следует

(5)

Подставив (5) в уравнение (3) и решив его относительно J, получим расчетную формулу для определения момента инерции маятника Максвелла относительно его оси симметрии

(6)

Отметим, что расчетная формула может быть получена также на основе законов динамики.

Выполняя данную лабораторную работу, Вы измерите время t падения маятника Максвелла с высоты h и на основе полученных данных рассчитаете его момент инерции. После этого Вам необходимо будет сравнить полученное значение момента инерции с теоретическим. Геометрические размеры и масса элементов маятника Максвелла приведены в таблице1.