Внутригодовые процентные начисления

В практике выплаты доходов на вложенный капитал нередко оговариваются величина годового процента и количество периодов начисления процентов. В этом случае расчет наращенной суммы FV„ ведется по формуле сложных процентов по

подынтервалам и но ставке, равной пропорциональной доле исходной годовой ставки, по формуле

(6.10)

где Р —  наращиваемая (т. е. исходная) сумма;

r   — объявленная годовая ставка;

т —  количество начислений в году;

и  — количество лет.

Вновь обращаем внимание читателя на то обстоятельство что в формулах наращения и дисконтирования должно соблюдаться соответствие между процентной ставкой и продолжительностью базисного периода  Так, переход от годового на числения процентов к квартальному (т = 4) предполагает переход к квартальной ставке, что как раз и имеет место в формуле (6 10)

Пример

В пожени лены и в банк в сумме 50 тыс руб на 2 года с полугодовым начис лением процентов, под 20% годовых В этом случае начисление процентов

проводится 4 раза по ставке 10% (20%/2),  а схема возрастания капитала будет иметь следующий вид

Период	Сумма, с которой идет начисление	Ставка (в долях ед )	Сумма к концу периода
6 мес	50 0	1,10	55,0
12 мен	55 0	1,10	605
18 мес	60 5	1,10	66 55
24 мес	66,55	1,10	73 205

Можно воспользоваться формулой (6.10). Поскольку т = % л = Z имеем

Консолидацией платежей

называется объединение нескольких платежей в один.

Сумма заменяемых платежей д.б. эквивалентна одному заменяющему платежу.

Пусть мы имеем серию платежей в размерах FV1, FV2, …, FV_m с соответствующими сроками  n1, n2,…,n_m. Заменяем эту серию платежей на один платеж в размере FV₀ и сроком уплаты n₀. Величина FV₀ неизвестна, но известен срок консолидированного платежа n₀.

Для определения FV₀ рассмотрим два варианта:

1. Срок n₀ находится внутри ряда n1, n2,…,n_m, т.е. n1<n₀< n_m. Пронумеруем платежи в интервале от  n1 до n₀ по j (FV_j, n_j), а в интервале от n₀ до n_m по к (FV_к, n_к). Тогда, разница в сроках определяется t_j=n₀-n_j, t_k=n_k-n₀. далее необходимо привести все платежи к единой временной точке. Возьмем в качестве такой точки время уплаты консолидированного платежа. Тогда

 

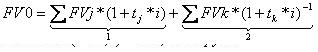
Первое слагаемое характеризует процессы наращения размеров платежей первоначальной серии, сроки уплаты которого д.б. наступить раньше срока консолидированного платежа.

Второе слагаемее выражает процессы дисконтирования размеров платежей, сроки которого наступают позже сроков консолидированного платежа.

1. Для срока n₀ верно  n₀>n_m . В этом случае консолидированный платеж производится позже последнего платежа первоначальной серии уплаты платежа. Поэтому существует одна операция наращивания

 

Конверсия платежей –

замена одних фин обяз-в другими на принципе фин эквивалентности.

Принцип фин эквивалентности заключается в неизменности фин взаимоотношений сторон в случае замены фин обяз-в. По-другому это означает, что при замене обяз-в в условиях конверсии ни один из участников сделки не должен получить дополнительной выгоды или потерпеть ущерб.

Конверсия платежей произ-ся в случаях:

- изменения сроков платежей

- замены первоначальной серии платежей на другую серию по суммам и срокам.

При проведении расчетов конверсии возможны различные варианты в т.ч. исп-е критического уровня % ставки.

При инвест анализе как частный случай конверсии исп-ся консолидация – объединение нескольких платежей в 1. Для опред-я размера консолидированного платежа сущ-ет тоже несколько вариантов.

Принцип эквивалентности необх-мо соблюдать в условиях, когда имеются различные варианты размещения фин ресурсов. В этом случае по спец формулам сравниваются различные % ставки, обеспечивающие равные фин рез-ты.

14