Соболева В.В. Лекции для студентов.

Математический анализ (Математика 2 часть) Лекция 1.

Тема I. Функции. Основные определения, теоремы и свойства.

Пределы. Производные и дифференциалы функций.

П.1. Функция. Определения и свойства.

Опр.1.Множество X всех допустимых действительных значений аргумента x, при которых функция y = f ( x ) определена, называется областью определения функции.

Опр.2 .Множество Y всех действительных значений y, которые принимает функция, называется областью значений функции.

Опр. 3. Определение функции: правило (закон) соответствия между множествами X и Y, по которому для каждого элемента из множества X можно найти один и только один элемент из множества Y, называется функцией.

Опр.4.Функция считается заданной, если: задана область определения функции X ; задана область значений функции Y ; известно правило ( закон ) соответствия, причем такое, что для каждого значения аргумента может быть найдено только одно значение функции. Это требование однозначности функции является обязательным.

Графиком функции y=f(x) называется множеств точек плоскости XOY с координатами (x,f(x)), где

Опр.5. Обра́тная фу́нкция — функция, обращающая зависимость, выражаемую данной функцией.

Функция является обратной к функции , если выполнены следующие тождества:

• f(g(y)) = y для всех

• g(f(x)) = x для всех

Опр.6. Сложная функция - функция от функции. Если величина y является функцией от u, то есть у = f (u), а и, в свою очередь, функцией от х, то есть u = u(х), то у является сложной функцией от х, то есть y = f [(x)], определённой для тех значений х, для которых значения u(х) входят в множество определения функции f (u).

В таком случае говорят, что у является сложной функцией независимого аргумента х, а u — промежуточным аргументом. Например, если у = u², u = sinx, то у = sin²х для всех значений х. Если же, например, у = , u = sinx, то у = , причём, если ограничиваться действительными значениями функции, сложная функция у как функция х определена только для таких значений х, для которых sin  0, то есть для , где k = 0, ± 1, ± 2,...

Опр.7.Монотонная функция. Если для любых двух значений аргумента x₁ и x₂ из условия x₂ > x₁ следует f ( x₂ ) > f ( x₁ ), то функция f ( x ) называется возрастающей; если для любых x₁ и x₂ из условия x₂ > x₁ следует f ( x₂ ) < f ( x₁ ), то функция f ( x ) называется убывающей. Функция, которая только возрастает или только убывает, называется монотонной.

Опр.8.Ограниченная и неограниченная функции. Функция называется ограниченной, если существует такое положительное число M, что | f ( x ) | M для всех значений x . Если такого числа не существует, то функция - неограниченная.

Опр.9.Непрерывная и разрывная функции. Функция y = f ( x ) называется непрерывной в точке x = a, если :

1) функция определена при x = a, т.e. f ( a ) существует;

2) существует конечный предел limx af(x) ;

3) f ( a ) = limx af(x)  .

Если не выполняется хотя бы одно из этих условий, то функция называется разрывной в точке x = a.

Опр.10.Если функция непрерывна во всех точках своей области определения, то она называется непрерывной функцией.

Опр.11. Чётная и нечётная функции. Если для любого x из области определения функции имеет место: f (  x ) = f ( x ), то функция называется чётной; если же имеет место: f (  x ) =  f ( x ), то функция называется нечётной. График чётной функции симетричен относительно оси Y ( рис.5 ), a график нечётной функции симметричен относительно начала координат ( рис.6 ).

Опр.12.Периодическая функция. Функция f ( x ) - периодическая, если существует такое отличное от нуля число T , что для любого x из области определения функции имеет место: f ( x + T ) = f ( x ). Такое наименьшее число называется периодом функции. Все тригонометрические функции являются периодическими.

Опр.13. Значение аргумента, при котором функция равна 0, называется нулём ( корнем ) функции. Функция может иметь несколько нулей. Например, функция y = x ( x + 1 ) ( x3 ) имеет три нуля: x = 0, x =  1, x = 3.

Геометрически нуль функции – это абсцисса точки пересечения графика функции с осью Х .

На рис.7 представлен график функции с нулями: x = a, x = b и x = c .

Опр.14.Асимптота. Если график функции неограниченно приближается к некоторой прямой при своём удалении от начала координат, то эта прямая называется асимптотой.

П.2.Элементарные функции.

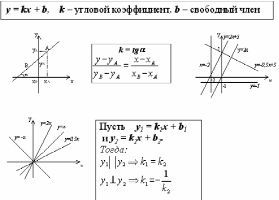
П.2.1. Линейной функцией называется функция  y = kx + b, где k  и  b - некоторые числа.

Прямопропорциональная зависимость между переменными x  и y приводит к простейшей линейной функции  y = kx.

Свойства линейной функции y = kx при k≠0  Область определения функции - множество R  всех действительных чисел. Корни - единственный корень x = 0. Промежутки постоянного знака зависят от знака параметра k: k > 0, то  y > 0 при x > 0 ; y < 0  при x < 0; k < 0, то  y > 0 при x < 0 ; y < 0  при x > 0. Экстремумов нет. Монотонность функции: если  k > 0, то y  возрастает на всей числовой оси; если k < 0, то y убывает на всей числовой оси. Наибольшего и наименьшего значений нет. Область значений - множество R. Четность - функция y = kx нечетная.

Графиком линейной функции y = kx является прямая, проходящая через начало координат. Коэффициент k называется угловым коэффициентом этой прямой. Он равен тангенсу угла наклона этой прямой к оси X: k = tg . При положительных  k этот угол острый, при отрицательных - тупой.

Графиком линейной функции y = kx + b тоже является прямая, смещенная на b единиц. Для построения графика достаточно двух точек. Например: A(0;b) B(−kb;0), если k≠0 . П.2.2. Переменные x и y связаны обратно пропорциональной зависимостью y=k/х , где k≠0, k - коэффициент обратной пропорциональности.

• Графиком обратной пропорциональности является кривая, состоящая из двух ветвей, симметричных относительно начала координат. Этот график называется гиперболой.

• Область определения функции функции y=k/х есть множество всех чисел, отличных от нуля, т.е D(f)=(− ;0) (0:+ )

• Гипербола не имеет общих точек с осями координат, а лишь сколь угодно близко к ним приближается.

• Если k > 0 , то ветви гиперболы в I и III координатных четвертях, если k < 0, то ветви гиперболы расположены во II и IV координатных четвертях координатной плоскости.

Рис. 7.

П.2.3. Квадратичная функция.

Функция, заданная формулой  y = ax² + bx + c , где x и y - переменные, а  a, b, c  - заданные числа, причем a≠0 , называется квадратичной функцией.

График квадратичной функции - парабола. Если a > 0 , то ветви параболы направлены вверх. Если a < 0 , то ветви параболы направлены вниз.

Рис. 8.

		Таблица 1.
Функция	y=ax2	y=ax2+bx+c
Область определения	R	R
Вершина параболы	(0;0)	(x0;y0);x0=−b2ay0=−4ab2−4ac
Нули функции	x = 0	при b2−4ac 0 x1 2=−b2a 2a b2−4ac  при b2−4ac 0 нулей нет
Экстремумы	минимум в вершине, если a > 0 максимум в вершине, если a < 0	минимум в вершине, если a > 0 максимум в вершине, если a<0
Область значений	0;+  , еслиa > 0 − ;0  , если  a < 0	y0;+  , если a > 0 − ;y0  , если  a < 0
Четность	четная	ни четная, ни нечетная

Расположение параболы на координатной плоскости

Рис. 9.

П. 2.4. Показательная функция.

При a > 0, a ≠ 1, определена функция y = a ^x , отличная от постоянной. Эта функция называется показательной функцией с основанием a.

Рис. 11.

Основные свойства показательной функции y = a ^x при a > 1:

• Область определения функции − вся числовая прямая.

• Область значений функции − промежуток (0;+  ) .

• Функция строго монотонно возрастает на всей числовой прямой, то есть, если x_{1 <}  x_{2 ,}  то a^x₁ <  a^x₂ .

• При  x = 0 значение функции равно 1.

• Если x > 0 , то a ^x >  1  и если x < 0, то  0 < a < 1.

Графики показательных функций с основанием 0 < a < 1 и   a > 1 изображены на рисунке.

Рис. 12.

Основные свойства показательной функции y = a ^x при 0 < a < 1:

• Область определения функции − вся числовая прямая.

• Область значений функции − промежуток (0;+  ) .

• Функция строго монотонно возрастает на всей числовой прямой, то есть, если x_{1 <}  x_{2 ,}  то a^x₁ >  a^x₂ .

• При  x = 0 значение функции равно 1.

• Если x > 0 , то 0 < a < 1 и если x < 0, то  a ^x >  1.

К общим свойствам показательной функции как при  0 < a < 1, так и при a > 1 относятся:

• a^x₁ a^x₂ = a^x_{1 +} ^x₂, для всех x₁ и  x_2.

• a−x=(ax)−1=1ax  для любого x.

• nax=axn  для  любого x и любого n N n≠1.

• (ab)^x = a^x b^x для любых a, b > 0;  a,b≠1.

• (ba)x=bxax   для любых a, b > 0;  a,b≠1.

• a^x₁ = a^x₂, то x₁ =  x_2.

П. 2.5. Степенная функция.

Степенной функцией с вещественным показателем a называется функция y  =  x ⁿ , x  > 0.

Заметим, что для натуральных n степенная функция определена на всей числовой оси. Для произвольных вещественных n это невозможно, поэтому степенная функция с вещественным показателем определена только для положительных x .

Рис. 13.

К основным свойствам степенной функции y  =  x ^a при a  > 0 относятся:

• Область определения функции − промежуток (0; +∞).

• Область значений функции − промежуток (0; +∞).

• Для любых a график функции проходит через точку (1; 1).

• Функция строго монотонно возрастает в области определения функции, то есть, если  x₁ < x₂ то a^r₁ < a^r₂ .

• График степенной функции при a  > 0 изображен на рисунке.

Рис. 14. рис. 15.

К основным свойствам степенной функции y  =  x ^a при a < 0 относятся:

• Область определения функции − промежуток (0; +∞).

• Область значений функции − промежуток (0; +∞).

• Для любых a график функции проходит через точку (1; 1).

• Функция строго монотонно возрастает в области определения функции, то есть, если  x₁ < x₂ то a^r₁ > a^r₂ .

• График степенной функции при a < 0 изображен на рисунке.

Справедливы следующие свойства степенной функции:

• x^a₁x^a₂ = x^a₁ ^{+ a}₂

• x^a₁ : x^a₂ = x^a₁ ^{- a}₂

•  (x^a₁)^a₂ = x^a₁ ^a₂

• x^a₁ > x^a₂,  x > 1,  a₁ > a₂

•   x^a₁ < x^a₂,  0 < x < 1,  a₁ < a₂

П.7. Функция квадратный корень.

Квадратный корень из числа a — это такое число, квадрат которого равен a, то есть решение уравнения  x² = a относительно переменной x.

Рис. 16. http://ru.wikipedia.org/wiki/%D0%98%D0%B7%D0%BE%D0%B1%D1%80%D0%B0%D0%B6%D0%B5%D0%BD%D0%B8%D0%B5:Square_root.pngГрафик функции y=  

Квадратным корнем называют также функцию   вещественной переменной  x, которая каждому x 0 ставит в соответствие арифметическое значение корня. Эта функция является частным случаем степенной функции x с a=1/2. Эта функция является гладкой при x > 0  , в нуле же она непрерывна справа, но не дифференцируема.

Свойства функции y=  

• Область определения - луч [о;+ ) . Это следует из, того что выражение   определено лишь при x 0.

• Функция y= x  ни четна, ни нечетна.

• Функция y= x  возрастает на луче [о;+ ) .

Свойства функции y= 3x 

• Область определения функции y= 3x  - вся числовая прямая

• Функция y= 3x  нечетна, так как 3−x=− 3x .

• Функция y= 3x  возрастает на всей числовой прямой.

Функция y= nx .

• При четном n функция y= nx  обладает теми же свойствами, что и функция y= x  и график ее напоминает график функции y= x .

• При нечетном n функция y= nx  обладает теми же свойствами. что и функция y= 3x , и график ее напоминает график функции y= 3x .

П.2.6. Абсолю́тная величина́ или мо́дуль, у= . В случае действительного аргумента — непрерывная кусочно-линейная функция, определённая следующим образом:

Имеют место также следующие формы записи данной функции:

.

• Область определения: .

• Область значений: .

• Функция чётная.

• Функция дифференцируема почти всюду.

• В точке x = 0 функция претерпевает излом, поэтому в этой точке функция недифференцируема.

П.2.7..Тригонометрические функции синус числа t и косинус числа t.

Если M(t) - точка числовой окружности, соответствующая числу t, то ординату точки M называют синусом числа t и обозначают sin t.

Если M(t) - точка числовой окружности, соответствующая числу t, то абсциссу  точки M называют косинусом числа t и обозначают cos t.

Свойства функций синус и косинус

• функция sin t нечетная: sin(-t) = - sin t, а функция cos t четная: cos(-t) = cos t;

• функции sin t и  cos t - переодические, 2 - основной период: sin(t 2 k)=sint и cos(t 2 k)=cost, где k - любое целое число;

• область значений функций sin t и  cos t - отрезок [ -1; 1];

• функция y = sin t возрастает на промежутках −2 +2 k;2 +2 k   и убывает на промежутках 2 +2 k;23 +2 k  , k Z;

• функция y = cos t убывает на промежутках 2 k;  +2 k   и возрастает на промежутках − +2 k;2 k  , k Z.

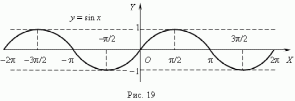
При построении тригонометрических функций мы используем радианную меру измерения углов. Тогда функция  y = sin x представляется графиком ( рис.19 ). Эта кривая называется синусоидой.   График функции  y = cos x представлен на рис.20; это также синусоида, полученная в результате перемещения графика  y = sin x  вдоль оси Х  влево на 2

П.2.8. Тригонометрические функции тангенс числа t и котангенс числа t.

Отношение sint/cost, где cost≠0, называют тангенсом числа t и обозначают tg t.

Отношение cost/sint, где sint≠0, называют котангенсом числа t и обозначают ctg t.

Свойства функций тангенс и котангенс.

• область определения функции tg t : x ≠2 + k k Z ;

• область определения функции ctg t : x ≠  k k Z ;

• функции tg t и ctg t нечетные: tg(-t) = - tg t   и  ctg(-t) = - ctg t;

• функции tg t и ctg t переодические, - основной период: tg(t k)=tgt ctg(t k)=ctgt;

• функция  y = tg t  возрастает на промежутках −2 + k;2 + k  ;

• функция  y = ctg t  убывает на промежутках   k;  + k  .

• Графики функций  y = tan x  и  y = cot x  показаны соответственно на рис.21 и рис.22