Свойства численных оценок параметров распределения

Смещенными называются оценки, математическое ожидание которых не равно оцениваемому параметру:

Несмещенными называются оценки, для которых – нет систематической ошибки в сторону занижения или завышения.

Оценка параметра а называется состоятельной, если она сходится по вероятности к оцениваемому параметру при

При ограниченном числе опытов , оценки несмещенные и состоятельные могут отличаться дисперсиями. Необходимо, чтобы дисперсия оценки была минимальной:

Оценка, обладающая таким свойством, называется эффективной.

Выборочное среднее и оценка дисперсии в случае равноточных измерений, статистическая дисперсия

Равноточные измерения – проводящиеся в одинаковых условиях.

Пусть и случайной величины Х неизвестны. Требуется на основе опытных данных найти состоятельные и несмещенные оценки этих параметров: ,

Покажем, что выборочное среднее является состоятельной и несмещенной оценкой мат. ожидания:

Согласно закону больших чисел:

Следовательно, являются состоятельной оценкой.

Статистическая дисперсия:

Проверим ее на состоятельность и несмещенность.

Правая часть сходится по вероятности к: значит, статистическая дисперсия является состоятельной оценкой дисперсии Dx.

Проверим, является ли несмещенной оценкой:

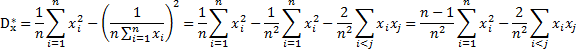
Выберем начало координат в точке

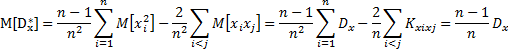
так как опыты независимы

Так как , то статитистическая дисперсия не является несмещенной оценкой для дисперсии Dx.

Определения и некоторые свойства распределений Пирсона, Стьюдента и Фишера

1. Случайная величина , по определению, равна сумме квадратов k независимых случайных величин каждая из которых имеет распределение N(0,1), то есть:

Распределение этой случайной величины называется распределением c k степенями свободы. Плотность этого распределения:

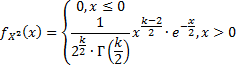
Среднее и дисперсия распределения равны соответственно:

2. Случайная величина T(k) есть отношение двух независимых случайных величин U и

Распределения случайной величины T(k) называется распределением Стьюдента с k степенями свободы:

Среднее M[T(k)]=0 и дисперсия D[T(k)]=

Свойства квантилей:

Распределение Стьюдента асимптотически нормально с нулевым средним и единичной дисперсией. При больших k (>30) используют соотношение

3. Случайная величина F(k1,k2) по определению равна отношению двух независимых случайных величин:

Распределение случайной величины называется распределением Фишера с k1 и k2 степенями свободы. Плотность распределения Фишера:

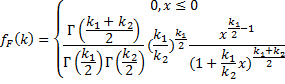
M[F]= , >2

Метод максимального правдоподобия

Один из наиболее распространенных методов нахождения оценок параметров. Пусть известны параметры:

В качестве оценок : принимают значения, удовлетворяющие условию максимума функции правдоподобия. Эти значения называют М П-оценками.

Пусть Х1, Х2… Хn выборка из генеральной совокупности объема n. Закон распределения выборки при этих конкретных значениях переменных Х1, Х2...Хn является функцией только неизвестных параметров : . Эта функция называется функцией правдоподобия и обозначается ).

Если определяют оценки параметров распределения дискретной случайной величины Х, а закон распределения имеет вид:

то функция правдоподобия равна вероятности того, что элементы выборки (независимые случайные величины Х1, Х2… Хn) примут конкретные значения Х1, Х2… Хn.

Для непрерывной случайной величины Х с плотность распределения: ) функция правдоподобия определяется так:

Для упрощения вычисления МП-оценок в некоторых случаях удобно рассматривать логарифм функции правдоподобия, т.е.

Оценки параметров, получаемые по методу максимального правдоподобия, асимптотически нормально распределены и для некоторых законов распределения генеральной совокупности имеют минимальную дисперсию.