Определение сходимости по вероятности

Пусть X1,X2...Xn последовательность С.В. – говорят, что эта последовательность сходится по вероятности к неслучайной величине а, если при вероятность события , (где – произвольно малое зафиксированное число) стремится к единице.

Каковы бы ни были произвольно малые наперед заданные числа и , всегда найдется такое большое число N, что для всех номеров, начиная с N:

Теорема Бернулли

При неограниченном возрастании числа n независимых опытов, в каждом из которых событие А появляется с вероятность Р, частоты события А сходятся по вероятности к его вероятности Р.

Доказательство:

Частота события:

Представим С.В. m в виде суммы индикаторов события А: , где

Частота – это среднее арифметическое n наблюдаемых значений С.В. Х-индикатора события А в одном опыте, (математическое ожидание индикатора события)

Согласно теореме Чебышева , что здесь все опыты в одинаковых условиях и вероятность появления события А во всех опытах одна и та же . Если вероятности P1, P2…Pn различны и производится неограниченное число n независимых опытов, вероятность события А в i-ом опыте

Теорема Чебышева I

Случайная величина Х с мат. ожиданием и дисперсией. Над С.В. Х проводится n независимых опытов, в результате которых она принимает значения X1, X2... Xn . Рассматривается среднее арифметическое всех этих значений, зависящих от n

Случайные величины Yn образуют последовательности, теорема утверждает, что последовательность Yn сходится по вероятности к мат. ожиданию С.В. Х:

Среднее арифметическое наблюдаемых в n независимых опытах значений случ. величины сходится по вероятности к её математическому ожиданию при

Доказательство:

Найдем математическое ожидание и дисперсию С.В. Х:

так как все С.В. Х распределены одинаково и имеют мат. ожидание Mx, то

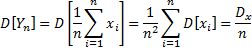
Применим к С.В. Yn неравенство Чебышева, в котором , где

Как бы ни мало было , всегда можно выбрать n таким большим, чтобы правая часть стала меньше сколь угодно малого тогда при достаточно большом n:

а вероятность противоположного события:

Это равносильно сходимости по вероятности Yn к мат. ожиданию:

Если С.В. Yn при сходится по вероятности к постоянной а, то это значит, что разность между Yn и а при сходится по вероятности к нулю:

В первой теореме Чебышева все Х1, Х2… Xn независимы, имеют одно и тоже распределение, одни и те же характеристики.

Теорема Чебышева II

Рассмотрим случай, когда условия независимых опытов меняются, то есть результаты – неограниченная последовательность независимых С.В. Х1, Х2… Хn с различным мат. ожиданием Mx:

Обозначим , докажем, что если все дисперсии ограничены сверху одним и тем же числом Д, то есть , то разность между средним арифметическим наблюдаемых значений С.В. – средним арифметическим их мат. ожидания сходится по вероятности к нулю:

Доказательство:

Согласно неравенству Чебышева:

Преобразуем:

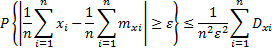
Учитываем, что все

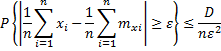
Как бы ни было мало произвольное наперед заданное , всегда можно выбрать n таким большим, чтобы правая часть стала меньше произвольного малого

Противоположное событие:

Теорема Пуассона

При разность между частотой события А и средним арифметическим его вероятностей сходится по вероятности к нулю:

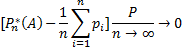
Доказательство: Теорема Пуассона есть следствие второй теоремы Чебышева:

– среднее арифметическое индикаторов события А в первом, во втором, в i-ом опытах, С.В. Х имеет мат. ожидание и

Дисперсии при любом i ограничены сверху одним и тем же числом D = 0.25 – это максимальное значение при p = ½

Применяя вторую теорему Чебышева к среднему арифметическому индикаторов, убедимся в справедливости т. Пуассона.