
- •Теория вероятностей и математическая статистика ymr0170
- •Оглавление
- •Теория вероятности
- •Аксиоматическое определение вероятности события:
- •Распределение вероятностей
- •Схемы выбора
- •Закон распределения с.В.
- •Биномиальное распределение
- •Распределение Пуассона
- •Обобщенное биномиальное распределение
- •Правило «трех сигм»
- •Числовые характеристики системы двух случайных величин
- •Ковариация
- •Коэффициент корреляции
- •Нормальный случайный вектор
- •Определение сходимости по вероятности
- •Теорема Бернулли
- •Теорема Чебышева I
- •Теорема Чебышева II
- •Теорема Пуассона
- •Центральная предельная теорема
- •Выборка и способы ее записи
- •Полигон, гистограмма частот, кумулятивная кривая
- •Числовые оценки параметров распределения
- •Свойства численных оценок параметров распределения
- •Выборочное среднее и оценка дисперсии в случае равноточных измерений, статистическая дисперсия
- •Определения и некоторые свойства распределений Пирсона, Стьюдента и Фишера
- •Метод максимального правдоподобия
- •Метод наименьших квадратов
Числовые характеристики системы двух случайных величин
 – начальный момент порядка kS
системы (X,Y)
– математическое ожидание
произведения степеней
– начальный момент порядка kS
системы (X,Y)
– математическое ожидание
произведения степеней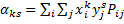 – начальный момент для
системы дискретных случайных величин
– начальный момент для
системы дискретных случайных величин
![]()
 – начальный момент для системы
непрерывных случайных величин
– начальный момент для системы
непрерывных случайных величин
![]()
Начальные моменты первого порядка – определяют координаты точки, называемые центром рассеивания системы на плоскости.
для системы дискретных случайных величин
для системы непрерывных случайных величин
![]()
Центральные моменты второго порядка – дисперсии характеризуют рассеивание случайной точки в направлении Ох и Оу.
Второй смешанный центральный
момент, ![]() – называется корреляционным моментом
или моментом связи. Характеризует
взаимное влияние случайных величин.
– называется корреляционным моментом
или моментом связи. Характеризует
взаимное влияние случайных величин.
 , безразмерное отношение – коэффициент
корреляции случайных величин Х и У.
, безразмерное отношение – коэффициент
корреляции случайных величин Х и У.
Теорема. Если случайные величины Х и У независимы, то корреляционный момент и коэффициент корреляции равны нулю.
Плотность распределения системы (Х,У) нормально распределенных и независимых случайных величин Х и У.
Каноническая форма нормального распределения на плоскости. Центр рассеивания совмещен с началом координат.
Ковариация
С.В.Д.Т.:
![]()
С.В.Н.Т.:
![]()
Свойства:
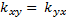 – симметричность
– симметричностьДисперсия случайной величины есть ковариация её с самой собой
Если Х и У независимы, то
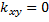


![]()


|

Доказательство: 
![]()
Коэффициент корреляции
Свойства:

Если Х и У независимы, то
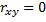
Если Y = aX+b – линейная зависимость, то
![]()
![]()
Если , то Х и У линейно зависимы У = aX+b, тогда:
![]()
То есть: ![]()
M[C] = C = M[![]() ]
= M[
]
= M[![]() ]-M[
]-M[![]() ]=
0-0=0
]=
0-0=0
C = 0, ![]()
Корреляционная матрица: ![]()
Нормальный случайный вектор
Двумерный случайный вектор (X,Y) распределен по нормальному закону, если совместная плотность распределения вероятностей случайного компонента (зависимых случайных величин) имеет вид:

Здесь
(![]() )
– центр рассеивания;
)
– центр рассеивания; ![]() – среднеквадратичные отклонения
случайных компонентов вектора (Х,У)
– среднеквадратичные отклонения
случайных компонентов вектора (Х,У)
Если компоненты двумерного нормального вектора некоррелированы ( ), то они независимы:
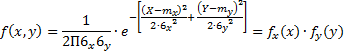
При
этом ![]() – главные оси рассеивания. Если
– главные оси рассеивания. Если ![]() – рассеивание называется круговым.
– рассеивание называется круговым.
Эллипс рассеивания
В
общем случае (![]() )
– эллипс рассеивания,
есть эллипс, в каждой точке которого
плотность имеет одно и то же постоянное
значение.
)
– эллипс рассеивания,
есть эллипс, в каждой точке которого
плотность имеет одно и то же постоянное
значение.

![]()
![]()
Ориентация эллипсов рассеивания зависит от коэффициента корреляции. С помощью преобразования поворота системы координат, плотность нормального распределения может быть приведена к каноническому виду с главным эллипсом рассеивания:
![]()
Свойства мат. ожидания функции случайной величины

![]()
![]()
![]()

![]()
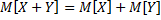 (как зависимых, так и независимых С.В.)
(как зависимых, так и независимых С.В.)
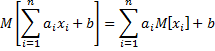
Мат. ожидание линейной функции случайных величин равно той же линейной функции от математических ожиданий этих величин.
Доказательство:
![]()
![]()
Отсюда:
![]()
Свойства дисперсии

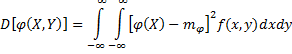
![]()
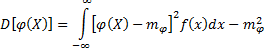

Удвоенная сумма корр. моментов каждой из слагаемых величин со всеми последующими

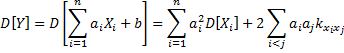
Дисперсия произведения двух независимых случайных величин
![]()
Дисперсия среднего арифметического n результатов измерений (независ. случайные величины от Х1 до Хn)

в n раз меньше дисперсия отдельного результата измерений.
Неравенство Чебышева
Для
любой С.В. Х, имеющей мат. ожидание
и дисперсию![]() ,
справедливо неравенство:
,
справедливо неравенство:
P{|![]()
где
любое положительное число (![]() ).
).
Неравенство ограничивает сверху вероятности больших отклонений С.В. от ее математического ожидания.
Доказательство: для С.В.Н.Т. с плотностью распределения вероятности f(x)
Первое
неравенство: ![]() ,
если дисперсия неизвестна
,
если дисперсия неизвестна
![]()
![]()

Дисперсия случайной величины Х:

Заменим
область интегрирования,
на множество точек, для которых ![]() ,
от этого интеграл
увеличится, не может:
,
от этого интеграл
увеличится, не может:
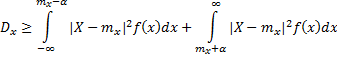
Заменим
![]() ,
не превосходящую
,
не превосходящую ![]() ,от этого выражения больше не станет:
,от этого выражения больше не станет:
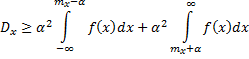
то есть:
![]() , делим обе части на
, делим обе части на ![]() , и получаем неравенство Чебышева.
Аналогично доказывается и для С.В.Д.Т.,
имеющей значения X1,X2...Xn
с вероятностями P1,P2...Pn,
вместо интегралов – суммы значений Xn
для которых
, и получаем неравенство Чебышева.
Аналогично доказывается и для С.В.Д.Т.,
имеющей значения X1,X2...Xn
с вероятностями P1,P2...Pn,
вместо интегралов – суммы значений Xn
для которых![]()
