Обобщенное биномиальное распределение
Если
вероятность осуществления события А
от испытания к испытанию меняется, то
формула Бернулли станет неприемлемой.
Пусть 
– вероятность успеха в k-ом
испытании в последовательности n
независимых испытаний
(
)
– вероятность неуспеха в k-ом
испытании. Тогда вероятность 
осуществления ровно m
успехов в n
испытаниях равна
коэффициенту при 
в разложении по степеням Х производящих
функций:
Искомые
коэффициенты
:
Полиномиальное распределение
В
каждом испытании теперь возможно r
различных исходов, и при n
испытаниях вероятность
исхода 
равна 
При
n испытаниях
вероятность того, что 
наблюдается
раз, 
раз … равна:
Равномерное распределение
С.В.Н.Т. х[a,b]
1. 
2. 
Вывод:
x < a | F(x) =
x > b | F(x) = 1
Показательное распределение
Случайная величина непрерывного типа распределена по показательному закону, если её плотность распределения вероятностей:
1.
2.
Функция распределения:
Вывод
1
2: 
3.
Математическое ожидание: 
Интегрируем по частям:
4.
Дисперсия: 
Функция
надежности: R(t) =
– вероятность не отказа любой системы
F(t) = 1- – откажет
5.
Среднеквадратичное отклонение: 
Нормальное распределение
Непрерывная случайная величина распределена по нормальному закону (закону Гаусса), если её плотность распределения вероятностей имеет вид:
Если
,
то нормальное распределение с такими
параметрами называется стандартным.
N(0,1)
Математическое ожидание:
M[x]
= 
Где
интеграл от 
есть
интеграл Пуассона, и он равен 
.
– интеграл от нечетной функции в
симметричных пределах, ответ 0.
Дисперсия:
Д[x]
= 
Вероятность
того, что случайная величина Х
распределенная по нормальному закону
N(
)
лежит в заданных пределах:
P
(
X
<
)
= 
Так
как 
не выражается через элементарные
функции, то пользуются таблицами значений
специальной функции Ф(х) называемой
функцией Лапласа или интегралом
вероятностей.
Свойства Ф(х):
1. Ф(0) = 0
2. Ф( ) = 1
Ф(
)
= 
3. Ф(-х) = -Ф(х) – нечетная функция
Правило «трех сигм»
Для
нормально распределенной случайной
величины Х со средним
и дисперсией 
:
P(|X-
|
< 3
)
= Ф(3) = 0.9973
Правило означает, что с большой вероятностью равно 0.9973, значения нормально распределенной случайно величины Х лежат в интервале:
(
3
3
)
Доказательство:
P(|X-
|<3
)
= P(
<
X<
)
= 
= 
P(|X- |< ) = Ф(1) = 0.6827
P(|X- |<2 ) = Ф(2) = 0.9545
P(|X- |<3 ) = Ф(3) = 0.9973
P(|X- |<4 ) = Ф(4) = 0.999936
Теорема Пуассона
Предположим,
что произведение np является
постоянной величиной, когда 
.
Обозначим 
,
тогда для любого фиксированного m
и для любого постоянного
Доказательство:
Рассмотрим еще одну приближенную формулу для вероятности Pn(m), когда n велико. В отличие от предыдущего случая число успехов m тоже растет с ростом n, а вероятность успеха постоянна.
Теорема Муавра-Лапласа (локальная)
Положим
.
Пусть 
,
и величины 
являются ограниченными. Тогда 
Замечание. При выводе используют формулу Стирлинга:
Рассмотрим
приближенную формулу для вероятности
того,
что событие А наступило не менее 
и не более 
раз в n
испытаниях, когда n
велико. Пусть 
растут с ростом n, а
вероятность успеха постоянна.
Теорема Муавра-Лапласа (интегральная)
Положим
,
Пусть
,
и величины 
,
являются ограниченными,
тогда:
Обозначим:
ф(х)
=
- функция Гаусса
Ф(х)
= 
– функция Лапласа (нечетная)
Значения функций ф(х) и Ф(х) находятся из таблицы. Тогда:
Локальная теорема Муавра-Лапласа утверждает, что:
Интегральная теорема Муавра-Лапласа, что:
,
где
,
Закон распределения функции случайного аргумента
1. Монотонная функция
Y
= 
:
известна f(x)
плотность распределения случайной
величины Х. Найти g(y)
плотность распределения
У.
, X = 
– обратная функция
Теорема: Линейное преобразование случайной величины не изменяет вида закона распределения:
Y = aX + b; a,b=const
Обратная
функция X = 
;
g(y)
= f(
)
2. Немонотонная функция
Неоднозначная
обратная функция: 
Система случайных величин
(Х, У) случайная точка, случайный вектор
Функция
распределения: F(x, y) =
P(X
x,
Y
y)
Свойства функции распределения системы случайных величин:
1.
2.
3.
4. 
5. 
Вероятность попасть в прямоугольник заданного размера есть плотность распределения системы двух случайных величин.
Поверхность распределения. Вероятность попадания случайной точки (X,Y) в область Д.
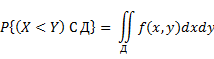
Объем цилиндрического тела, ограниченного поверхностью распределения над областью Д.
Свойства f(x,y):
т.к.
то плотности распределения отдельных величин, входящих в систему:
