
- •Теория вероятностей и математическая статистика ymr0170
- •Оглавление
- •Теория вероятности
- •Аксиоматическое определение вероятности события:
- •Распределение вероятностей
- •Схемы выбора
- •Закон распределения с.В.
- •Биномиальное распределение
- •Распределение Пуассона
- •Обобщенное биномиальное распределение
- •Правило «трех сигм»
- •Числовые характеристики системы двух случайных величин
- •Ковариация
- •Коэффициент корреляции
- •Нормальный случайный вектор
- •Определение сходимости по вероятности
- •Теорема Бернулли
- •Теорема Чебышева I
- •Теорема Чебышева II
- •Теорема Пуассона
- •Центральная предельная теорема
- •Выборка и способы ее записи
- •Полигон, гистограмма частот, кумулятивная кривая
- •Числовые оценки параметров распределения
- •Свойства численных оценок параметров распределения
- •Выборочное среднее и оценка дисперсии в случае равноточных измерений, статистическая дисперсия
- •Определения и некоторые свойства распределений Пирсона, Стьюдента и Фишера
- •Метод максимального правдоподобия
- •Метод наименьших квадратов
Закон распределения с.В.
Соотношение вероятностей и их соответствующее значение (табличный ряд распределения случайной величины)
Функция
распределения: F(x)
= P(X
< x), C.B.
X - вероятность того, что
случайная точка Х в результате опыта
попадает левее (![]() )
х (интегральный закон распределения),
f(x) – скорость
изменения (производная)
)
х (интегральный закон распределения),
f(x) – скорость
изменения (производная)
Свойства:
0
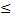 F(x)
F(x)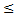 1
1P(
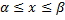 )
= F(
)
= F(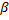 )
– F(
)
– F(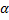 )
– вероятность С.В. попасть в интервал
[
)
– вероятность С.В. попасть в интервал
[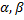 ]
]F(
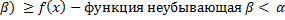
F(
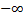 )
= 0
)
= 0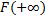 = 1
= 1
Плотность
распределения вероятностей:
![]()
Свойства:
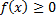
F(x) = P(X < x) =
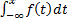
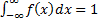 (условие нормировки)
(условие нормировки)f(x) = F’(x), F(x) – функция распределения вероятностей
P(
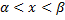 )
=
)
=  – вероятность попасть
Х на участке (
)
– вероятность попасть
Х на участке (
)
Вероятность попасть в точку (С.В.Н.Т.) = 0.
Условие нормировки – площадь под всей кривой распределения равен 1.
Математическое ожидание – действительное число, определяемое в зависимости от типа С.В. Х:
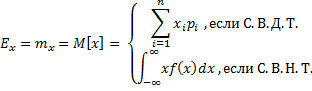
Мода
![]() – действительное число,
определенное как точка максимума
плотности распределения вероятности
f(x).
– действительное число,
определенное как точка максимума
плотности распределения вероятности
f(x).
Медиана – равновероятное получение большего или меньшего значения С.В.
P(X
< ![]() )
= P(X
)
= P(X ![]() )
или F(
)
=
)
или F(
)
= ![]()
Дисперсия С.В. – математическое ожидание квадрата отклонения от ее математического ожидания.
Д[x]
= M[![]() ]
или Д = М[
]
или Д = М[![]() ]
-
]
- ![]()
Д[x]
= ![]()
Среднее
квадратичное отклонение:
![]() = Д[x] –
определяет стандартный среднеквадратичный
интервал рассеивания.
= Д[x] –
определяет стандартный среднеквадратичный
интервал рассеивания.
центрированная С.В.:
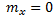
стандартизированная С.В.:
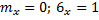
Свойства дисперсии:
если Х – const, то
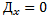
Д[C
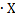 ]
=
]
= 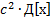

Доказательство:
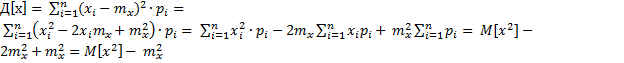 (для С.В.Д.Т.)
(для С.В.Д.Т.)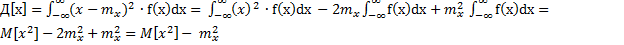 (для С.В.Н.Т.)
(для С.В.Н.Т.)
Начальный
момент k-го
порядка –
математическое ожидание величины ![]()
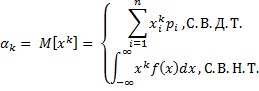
Центральный
момент k-го
порядка
случайной величины Х называется
математическое ожидание величины ![]()
![]()
![]()
![]() характеризует скошенность (асимметрию)
распределения (если f(x)
симметрична относительно
характеризует скошенность (асимметрию)
распределения (если f(x)
симметрична относительно ![]() ,
то
,
то ![]() )
)
![]()
![]() – островершинность
(плосковершинность)
– островершинность
(плосковершинность)
![]() (эксцесс
- безразмерная величина). Островершинные
имеют положительный эксцесс, плосковершинные
отрицательный. 3 – соответствует
нормальному распределению (распределение
Гаусса)
(эксцесс
- безразмерная величина). Островершинные
имеют положительный эксцесс, плосковершинные
отрицательный. 3 – соответствует
нормальному распределению (распределение
Гаусса)
![]() – абсолютный начальный
момент
– абсолютный начальный
момент
![]() – абсолютный центральный
момент (первый совпадает со средним
арифметическим отклонением)
– абсолютный центральный
момент (первый совпадает со средним
арифметическим отклонением)
Квантиль
р(порядка)
– распределение случайной величины Х
непрерывного типа – действительное
число ![]() , удовлетворяющее уравнению:
, удовлетворяющее уравнению:
P(X
< ![]() )
= p
)
= p
P(|X|
<![]() )
= p
)
= p
В
частности, ![]()
Критической
точкой порядка р
– называется распределение случайной
величины Х непрерывного типа –
действительное число ![]() (x-каппа),
удовлетворяющее уравнению:
(x-каппа),
удовлетворяющее уравнению:
P(X
![]() )
= p
)
= p
P(|X|
![]() )
= p
)
= p
Квантиль
и критическая точка связаны между собой:
![]()
![]() – биномиальное распределение (n
– число испытаний, р –
вероятность 1 испытания)
– биномиальное распределение (n
– число испытаний, р –
вероятность 1 испытания)
![]() – равномерное распределение на интервале
а,b
– равномерное распределение на интервале
а,b
![]() – нормальное распределение
– нормальное распределение
Биномиальное распределение
P(x=m)
= ![]() (q = 1-p; n = 0,1,2...n)
(q = 1-p; n = 0,1,2...n)
![]() – С.В.Д.Т.
– С.В.Д.Т.
Вывод:
![]()
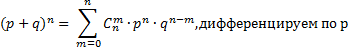
![]() ,
умножим на р
,
умножим на р
![]() ,
,
![]()
= n p
![]() – дисперсия биномиального распределения
– дисперсия биномиального распределения
Вывод:
![]()
![]() ,
дифференцируем по р, (дважды)
,
дифференцируем по р, (дважды)
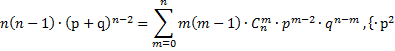
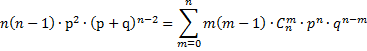
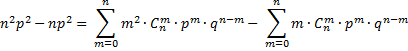
![]()
![]()
![]() – среднеквадратическое
отклонение (для биномиального
распределения)
– среднеквадратическое
отклонение (для биномиального
распределения)
Распределение Пуассона
-
аппроксимирует биномиальное распределение
при ![]() при условии, что np имеет
конечный предел
(закон малых чисел)
при условии, что np имеет
конечный предел
(закон малых чисел)
![]()
Отрезок
оси ![]() длины l,
точек m.
длины l,
точек m.
![]() – среднее число точек (математическое
ожидание) приходящееся на единицу длины
– среднее число точек (математическое
ожидание) приходящееся на единицу длины
![]()
отсюда a = np;
Вывод:

![]()
![]()
![]()
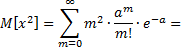
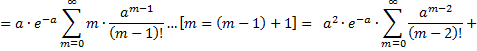
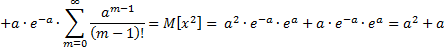
![]()
![]()
![]()
Основные характеристики биномиального распределения:
![]()
