Теория вероятностей и математическая статистика ymr0170

Преподаватель: Светлана Бабиченко

Оглавление

Теория вероятности 3

Аксиоматическое определение вероятности события: 3

Распределение вероятностей 3

Схемы выбора 4

Формула полной вероятности 5

Формула Бейеса(Bayes) 5

Формула Бернулли 6

Случайная величина 6

Закон распределения С.В. 6

Биномиальное распределение 11

Распределение Пуассона 12

Обобщенное биномиальное распределение 13

Полиномиальное распределение 13

Равномерное распределение 14

Показательное распределение 15

Нормальное распределение 16

Правило «трех сигм» 17

Теорема Пуассона 18

Теорема Муавра-Лапласа (локальная) 18

Теорема Муавра-Лапласа (интегральная) 19

Закон распределения функции случайного аргумента 19

Система случайных величин 20

Свойства функции распределения системы случайных величин: 20

Числовые характеристики системы двух случайных величин 22

Ковариация 23

Коэффициент корреляции 24

Нормальный случайный вектор 25

Эллипс рассеивания 26

Свойства мат. ожидания функции случайной величины 26

Свойства дисперсии 27

Неравенство Чебышева 28

Определение сходимости по вероятности 29

Теорема Бернулли 29

Теорема Чебышева I 30

Теорема Чебышева II 32

Теорема Пуассона 33

Центральная предельная теорема 33

Выборка и способы ее записи 34

Полигон, гистограмма частот, кумулятивная кривая 34

Числовые оценки параметров распределения 35

Свойства численных оценок параметров распределения 36

Выборочное среднее и оценка дисперсии в случае равноточных измерений, статистическая дисперсия 37

Определения и некоторые свойства распределений Пирсона, Стьюдента и Фишера 38

Метод максимального правдоподобия 39

Метод наименьших квадратов 40

Теория вероятности

Случайный исход – множество элементарных исходов опыта Ω.

Поле событий F – совокупность всех наблюдаемых событий.

A B событие А влечет за собой событие В, если А влечет В, а В влечет А, то А=В

• A B <=> A+B – объединение множеств (логическое «или»)

• A B – пересечение множеств (или их произведение)

• A-B, A\B – разность событий (А произошло, В нет)

• дополнение множества A = Ω - A (A не происходит)

Аксиоматическое определение вероятности события:

Р(А). Пусть F – поле события заданного эксперимента. Вероятностью Р(А) называется числовая функция, определенная для всех A F и удовлетворяющая трем аксиомам:

1. Р(А) 0

2. Р(Ω) = 1

3. P( ) =

Пусть , тогда совокупность { } – является разбиением. Тогда в силу 2 и 3 свойства:

P( ) + P( ) + ... + P( ) = 1 – единичная вероятность достоверного события распределяется по множеству несовместных событий, образующих полную группу.

Распределение вероятностей

Соответствие. Опыт повторяется n раз, при этом событие A произошло m раз, тогда P*(A) = – это относительная частота осуществления события А.

Классическая вероятность - это всякий эксперимент с соответствующим ему конечным Ω множеством равновероятных исходов.

P( ) = P( ) = ... = P( ) =

P(А) = – формула классической вероятности.

Схемы выбора

1. Сочетание: =

Выбор без возвращения и упорядочивания. Свойства биномиальных коэффициентов:

• Асимметрия:

• Рекуррентное соотношение:

• 

2. Размещение: =

Размещение без возвращения, но с упорядочиванием.

3. Сочетание с повторением:

Выбор с возвращением m элементов множества E без упорядочивания.

4. Размещение с повторением:

5. Схема упорядоченных разбиений:

Разбиение множества Е (с n элементами) по S подмножествам.

6. Геометрическая вероятность: P(A) =

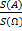
Безусловная вероятность – числовая функция, определенная на поле событий для данного эксперимента, не зависит от условий, удовлетворяющим трем аксиомам.

Условная вероятность: Р(В/А) = , Р(А) > 0 (обязательно условие, что событие А происходит одновременно с событием В)

Вероятность произведения событий (формула умножения): P(AB) = P(A) ∙ P(B/A) = P(B) ∙P(A/B)

Формула умножения вероятностей для произвольного числа событий: P( ) = P( )∙ P( ) ∙ P( .. )

Событие А независимо от события В, если P(A/B) = P(A), P(B) > 0

События называются независимыми, если Р(АВ) = P(A) ∙ P(B)

События называются независимыми в совокупности, если (m = 2,3...n) для любого набора из m событий выполняется равенство: = P( P( ∙... ∙ P(

Вероятность суммы событий (формула сложения): P(A+B) = P(A) + P(B) - P(AB), если А и В независимы, то аксиома сложения: P(A+B) = P(A) + P(B), т.к. P(AB) =

Вероятность суммы событий (общая формула): P( ) = - + + ∙

Формула полной вероятности

Р(А) =

Формула Бейеса(Bayes)

- совокупность гипотез по отношению к событию А, и А – событие осуществилось.

= , где Р(А) =

Формула Бернулли

=

Биномиальное распределение

= =

= + p +...+

p – есть вероятность, что событие А происходит при одном испытании.

Производящая функция:

f(x) – плотность распределения вероятности: p(x)

Случайная величина

Принимает то или иное значение (одно единственное)

• Дискретная случайная величина - конечное, либо бесконечное счетное множество значений (число выстрелов до первого попадания)

С.В.Д.Т.: P(X= ) = P(X= ) = , несовместные события образующие полную группу.

• Непрерывная случайная величина – заполняют некоторый интервал числовой оси (число возможных С.В.Н.Т. бесконечно)

С.В.Н.Т.: F(x) = P(X < x)