5.2 Похибки визначення ліній положення радіонавігаційних систем

Похибка визначення поверхні (лінії) положення оцінюють відрізком нормалі між поверхнями (лініями) положення, що відповідають щирому й обмірюваному значенням РНП.

Рівняння РНП у декартовій системі координат можна записати у виді р=р(х, у, z) у просторі і р=р(х, у) на площині. Ці рівняння відповідають тривимірному і двовимірний скалярним полям параметра р. У межах робочих зон РНС функція р(х, у, z) безупинна і диференційована, тому зміна скалярного полючи РНП можна описати його градієнтом gradp, тобто вектором, що показує напрямок найшвидшого росту параметра р.

Якщо 1-одиничний вектор, спрямований уздовж нормалі до поверхні (лінії) положення убік росту р, то скалярний добуток

1grad(p) = dp/dl.

Модуль градієнта g=\gradp\ = \dp/dl\ дозволяє зв'язати похибка виміру РНП р з погрішністю фіксації поверхонь (ліній) положення l:

l= р/g. (5.1)

З цього рівняння випливає, що точність визначення поверхонь (ліній) положення збільшується з ростом точності виміру і модуля градієнта полючи РНП.

Якщо функції р(х, у, z) чи р(х, у) задані аналітично, то модуль градієнта для поверхні положення та лінії положення відповідно становлять:

Скориставшись приведеними співвідношеннями, оцінимо похибка визначення ліній положення для дальномірного кутомірних і разницево-дальномірного методів місцезнаходження.

У дальномірних системах виміряється час затримки сигналу t_в. Цей час зв'язаний з навігаційним параметром D формулою D = сt_в для дальноміра без запиту і D = сt_в/2 для дальноміра з запитом, активної РЛС з активною чи пасивною відповіддю і радіовисотоміра.

При вимірі дальності лінії положення мають форму кіл радіусом D (рис. 5.1) при розташуванні РНК в крапці О, а об'єкта — у крапці М. Знайдемо середньоквадратичне значення похибки визначення лінії положення , якщо похибка виміру РНП становить . В обраній системі координат , p = D. Згідно (5.2), g = \grad\= 1 і l==l. Звідси випливає, що

, (5.2)

де _D — середньоквадратичне значення похибки виміру D, — середньоквадратичне значення похибки виміру затримки сигналу за часом; с — швидкість поширення радіохвиль.

У кутомірних РНС вимірюваним РНП є кут ос (рис. 5.2), а похибка його виміру . Лінією положення буде пряма ОМ

Знайдемо середньоквадратичну похибка визначення лінії положення . При р =  = arctg(x/.y) з урахуванням (5.2) і рис. 5.2 знайдемо

Тоді відповідно до (5.1) l = /g__, отже, _l=D_

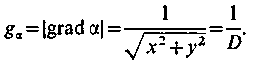
У разницево-дальномірних РНС вимірюваним параметром є різниця відстаней p = D_Р = D_A—D_B об'єкта від ведучої А и відомої В станцій з відстанню між ними (базою) d (рис. 5.3). Тут лінія положення-гіпербола, а  – кут, під яким із крапки розташування об'єкта М видна база. Згідно рис. 5.3, .