3. Практические занятия

Практическое занятие №1

Тема: Расчетные методы определения физико-химических свойств

И состава нефти и нефтепродуктов

Плотность и удельный вес. Количества вещества – массы, заключенной в единице объема, называется плотностью. Плотность измеряется в кг/м³ и г/см³. Плотность нефтепродуктов зависит от температуры, от углеводородного и фракционного состава. С увеличением содержания ароматических углеводородов в нефтепродуктах плотность последних возрастает. С повышением температуры плотность нефтяных фракций понижается.

Отношение плотности нефтепродукта при 20 °С к плотности дистиллированной воды при 4 °С называется относительной плотностью. Относительная плотность нефтепродуктов при температуре t °С определяется по формуле Д.И. Менделеева:

(1.1)

где - относительная плотность нефтепродукта при 20 °С;

- коэффициент объемного расширения, зависящий от температуры и плотности нефтепродукта;

t – температура в °С.

В технических расчетах можно использовать для определения плотности нефтепродуктов при высоких температурах графиком.

Плотность смеси нефтепродуктов определяется по формуле

(1.2)

где х₁, х₂, х₃, …х_п – весовые доли компонентов смеси;

… - плотности компонентов смеси.

Сила притяжения единицы объемы вещества к Земле называется удельным весом. Удельный вес измеряется в кГ/м³ и Г/м³. Удельный вес зависит от ускорения силы тяжести в точке измерения.

Плотности жидкости и ее удельный вес связаны следующей зависимостью:

(1.3)

где g – ускорение силы тяжести, равное приблизительно 9,81 м/сек².

Вязкость. Вязкостью называется внутреннее трение жидкости, возникающее между молекулами при их перемещении. Различают вязкость динамическую, кинетическую, удельную и условную.

Свойство жидкости оказывать сопротивление сдвигающим ее силам называется динамической вязкостью . Динамическая вязкость жидкости обусловливается силами сцепления между молекулами и по величине равна силе, препятствующей их перемещению. За единицу динамической вязкости принимается пуаз (пз), равный вязкости такой жидкости, в которой сила в 1 дину перемещает слой жидкости площадью 1 см², находящийся на расстоянии 1 см от другого слоя со скоростью 1 см/сек.

Кинетическая вязкость называется отношение динамической вязкости к плотности жидкости при той же температуре:

, (1.4)

Удельной вязкостью называется отношение динамической вязкости данной жидкости (нефтепродукта) к динамической вязкости воды:

, (1.5)

Где - динамическая вязкость жидкости (нефтепродукта);

- динамическая вязкость дистиллированной воды.

Условная вязкость в градусах (°ВУ) представляет собой отношение времени истечения 200 см³ нефтепродукта при температуре испытания t °С ко времени истечения 200 см³ дистиллированной воды при температуре 20 °С в одном и том же вискозиметре.

Условная вязкость нефтепродуктов переводится в кинетическую или динамическую по формулам:

; (1.6)

(1.7)

Вязкости нефти и нефтепродуктов зависят от температуры и углеводородного состава. С.А. Гроссом предложена эмпирическая формула для определения кинетической вязкости нефтепродуктов при любой температуре, если известны их вязкости при двух различных температурах, т.е.

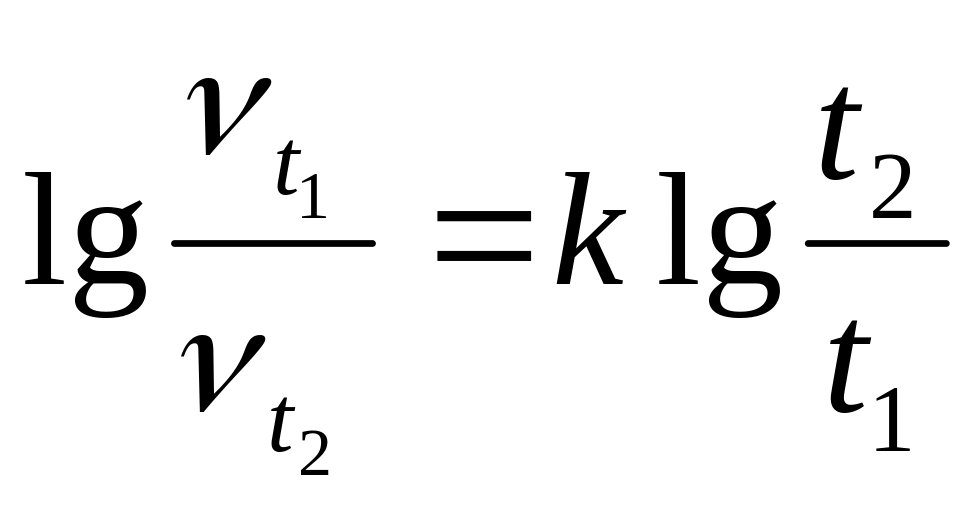, (1.8)

где - кинетическая вязкость нефтепродукта при t₁ °С;

- кинетическая вязкость нефтепродукта при t₂ °С;

k – коэффициент, характеризующий данный нефтепродукт.

Молекулярный вес. Молекулярный вес вещества показывает во сколько раз одна молекула данного вещества тяжелее одного атома водорода или 1/16 части атома кислорода. Зная химическую формулу молекулы вещества, т.е. сколько тех или иных атомов содержится в его одной молекуле, нетрудно определить его молекулярный вес.

Для нефтяных фракций, которые представляют собой смесь большого числа молекул различных углеводородов, молекулярный вес определяют опытным путем или рассчитывают по формулам. Б.П. Воиновым предложена следующая формула для определения молекулярного веса нефтепродукта:

М=60+0,3t+0,001t² (1.9)

где t – средняя температура кипения нефтепродуктов.

Результаты вычисления по этой формуле расходятся с лабораторными определениями на 3-5 %. Средняя температура кипения узких фракций определяется как средняя арифметическая температура:

, (1.10)

где t_Н и t_К – температуры начала и конца кипения нефтяной фракции.

Средняя объемная температура кипения широкой фракции может быть вычислена, если известны результаты разгонки нефтепродуктов в стандартных условиях, по формуле:

, (1.11)

где t₁₀, t₂₀,…, t₉₀ – температура отгона 10, 20, …, 90% объем. фракции.

Определение весового, объемного и молекулярного состава смеси. Свойства жидкого раствора или смеси газов зависят как от свойств отдельных компонентов, так и от их относительного содержания, т.е. концентрации. Различают концентрации весовые, объемные и молекулярные, каждую из которых можно выразить в процентах или в долях единицы.

Пусть нефтяная смесь состоит из двух компонентов (бинарная смесь), молекулярные веса которых соответственно равны М₁ и М₂, а массы их – g₁ и g₂; общая масса g= g₁ + g₂.

Под весовой концентрацией компонента понимают отношение массы данного компонента к массе всей смеси. Для нашего случая весовые концентрации будут:

х₁= х₂= (1.12)

Сумма весовых концентраций равна единице:

х₁ + х₂= (1.13)

Для определения числа киломолей отдельных компонентов смеси необходимо знать молекулярные веса и количество (массу) отдельных компонентов (фракций). Разделив массу каждого компонента на его молекулярный вес, получим соответственно число киломолей первого и второго компонентов:

и (1.14)

Общее число киломолей равно

(1.15)

Молекулярной концентрацией данного компонента в смеси называется отношение числа киломолей данного компонента к общему числу киломолей смеси, т.е.

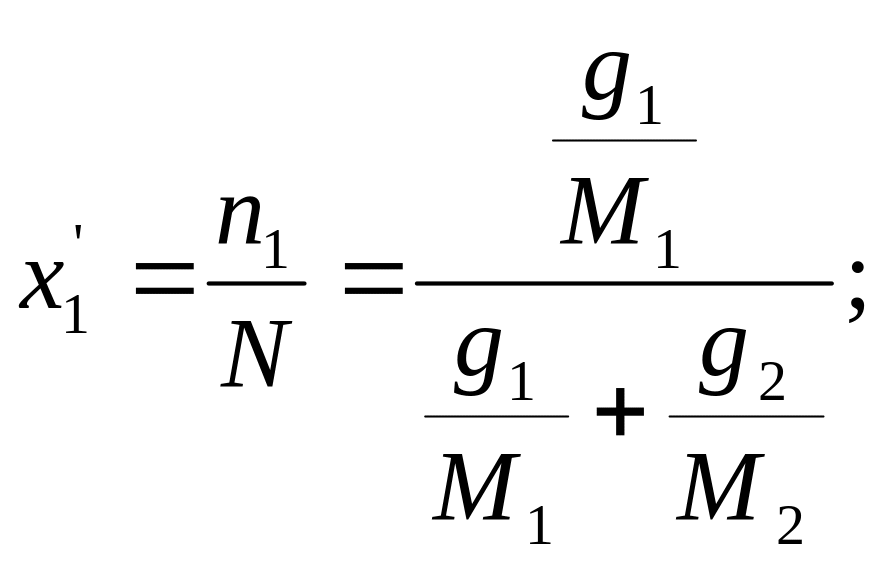
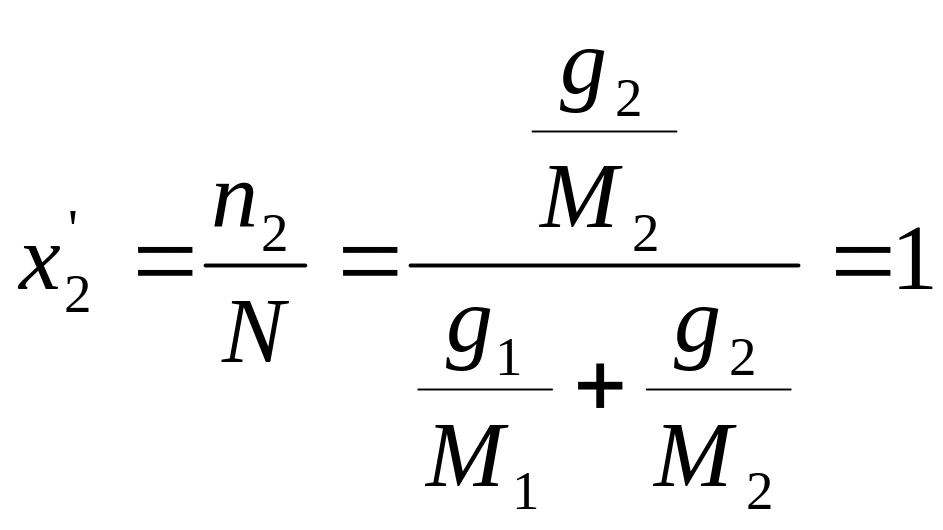(1.16)

Сумма этих концентраций также равна единице:

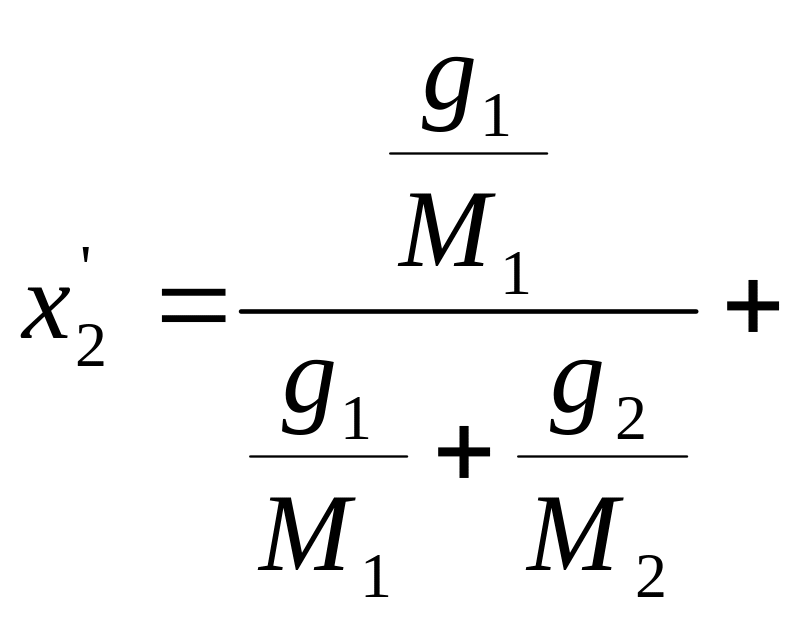
(1.17)

Средний молекулярный вес данной двухкомпонентной смеси определяется следующей формулой:

(1.18)

Если известны молекулярные концентрации отдельных компонентов, то средний молекулярный вес смеси определяется формулой:

(1.19)