Лабораторное занятие 2.2

Разрешение проблем безубыточности деятельности предприятия

Цель: изучить основы маржинального анализа во всем многообразии условий и моделей; закрепить практические навыки решения задач управления количественными методами с использованием возможностей Excel

План лабораторного занятия:

• Изучить теоретические основы маржинального анализа (CVP-анализа)

• Рассмотреть бухгалтерскую модель безубыточности

• Изучить изменение модели безубыточности при ограниченном спросе

• Закрепить навыки использования корреляционно-регрессионного анализа при изучении поведения затрат предприятия и соотношения их величины с выручкой и объемом производства с использованием возможностей Excel

Этапы и содержание

1. Теоретическая часть Теоретические основы анализа безубыточного производства

Анализ безубыточности предусматривает системное исследование взаимосвязи таких показателей, как затраты, объём реализации и прибыль

Отдельно определяются:

- объём реализации, который обеспечивает осуществление всех затрат и получение желаемой прибыли;

- величина прибыли при заданном объёме реализации;

- влияние на прибыль изменений величины затрат, объёма и цены реализации;

- оптимальная структура затрат и т.п.

Безубыточность – это такое состояние деятельности предприятия на отчётный период, на протяжении которого, предприятие не получает прибыли, а только полученными доходами покрывает все расходы.

Анализ безубыточности в литературе также называют анализом взаимосвязи «затрат-объёма-прибыли» (с англ.Cost-Volume-Profit) или СVP-анализ.

Результаты такого анализа являются основанием для обоснования выбора управленческих решений, относительно ассортимента и маркетинговой политики. Однако наибольшее значение данный анализ играет для определения объёма производства и его критической точки – точки безубыточности.

Бухгалтерская модель безубыточности

Допущения:

1. Спрос неограничен

2. Цена продажи продукции неизменна и устраивает потребителей

3. Цена покупки ресурсов неизменна

4. С увеличением объёма производства величина административных, не распределяемых общепроизводственных, прочих расходов остаётся постоянной.

Так как цена на продукцию неизменна, и спрос неограничен, каждая новая единица изделия будет находить своего покупателя и увеличивать доход предприятия на цену продажи продукции (P). Таким образом, зависимость между доходом (TR) и объёмом производства (Q) – положительна и прямолинейная и определяется по формуле:

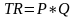, (2.2.1)

В связи с 4-ым допущением все расходы (TC) строго делятся на постоянные (FC) – зависящие от Q и переменные (VC) – не зависящие от Q.

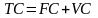, (2.2.2)

Переменные расходы на одно изделие называются средними переменными расходами (AVC) и определяются отношением всех переменных расходов к объёму производства по формуле:

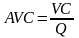, (2.2.3)

Так как цена ресурсов неизменна, то как постоянные (FC), так и переменные расходы на одно изделие (AVC) не меняются со временем. Следовательно, исходя из формулы 2.2.2 и 2.2.3

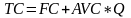, (2.2.4)

Так как точкой безубыточности назван объём производства при котором прибыль равняется нулю, то, в данной модели, таким объёмом будет такой Q (назовём его количеством реализованной продукции в точке безубыточности Q_b), при котором разница общих доходов и расходов будет равна нулю.

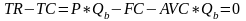, (2.2.5)

Исходя из формулы 2.2.5, можно сделать вывод, что величина критического объёма производства зависит от величины постоянных расходов и разницы между ценой и средними переменными расходами. Чем больше FC, тем больший Q необходим, чтобы их компенсировать. Чем больше разница между P и AVC, тем меньший Q необходим, чтобы покрыть постоянные расходы.

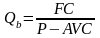, (2.2.6)

В связи с важностью разницы между ценой и средними переменными расходами, в бухгалтерской модели её выделяют в отдельный показатель маржинальный доход – СM_ед, который в литературе также называется граничным доходом, единичной прибылью покрытия.

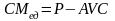, (2.2.7)

Таким образом, формулу 2.2.6 можно записать в следующем виде

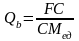, (2.2.8)

Маржинальный доход отражает меру увеличения прибыли от производства дополнительной единицы изделия: при увеличении производства на одно изделие, доходы растут на величину P, а расходы на величину AVC (постоянные расходы неизменны), следовательно прибыль вырастет на разницу выросших доходов равных P и выросших расходов равных AVС, то есть вырастет на величину маржинального дохода (СМ_ед). Следовательно, можно прогнозировать прирост прибыли при увеличении объёма производства по формуле:

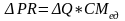, (2.2.9)

Из формулы 2.2.9, не сложно узнать как рассчитать количество продукции, которое нужно дополнительно произвести, чтобы получить необходимый прирост прибыли

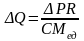, (2.2.10)

Теперь мы имеем возможность рассчитать величину объём продукции, который необходим для достижения заданной величины прибыли. Чтобы добиться прибыли PR необходимо вначале достигнуть точки безубыточности (где прибыль равно нулю), а потом ещё увеличить объём настолько, чтобы прирост прибыли достиг заданной величины PR.

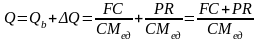, (2.2.11)

Из формулы 2.2.11 можно выделить прибыль

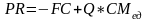, (2.2.12)

Из формулы 2.2.12 можно сделать интересные выводы. Если на предприятии провести регрессионный анализ линейной зависимости прибыли от объёма производства, то мы получим регрессионную модель 2.2.13, в которой случайный член «а» в идеале должен соответсвовать «-FC», а регрессионный коэффициент «b» равен маржинальному доходу.

Если

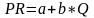, (2.2.13)

то, при правильности бухгалтерской модели безубыточности 2.2.12

,

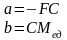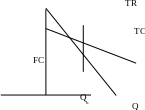
У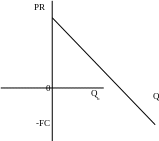 словная графическая бухгалтерская модель безубыточности имеет вид