Федеральное агентство по образованию

Государственное образовательное учреждение высшего профессионального образования

ВЯТСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ

Кафедра электропривода и автоматизации

промышленных установок

СИНТЕЗ АРИФМЕТИКО-ЛОГИЧЕСКОГО УСТРОЙСТВА РЕАЛИЗОВАННОГО НА ЭЛЕМЕНТАХ ЦИФРОВОЙ ТЕХНИКИ

Методические указания для курсового проекта по курсу "Автоматизация и оптимизация технологических процессов"

Для студентов дневной и заочной формы ускоренного обучения специальности 180400 "Электропривод и автоматика промышленных установок и технологических комплексов"

Киров 2008

УДК 681.3(075)

А 75

Печатается по решению редакционно-издательского совета

Вятского государственного университета

Рецензент: кандидат технических наук,

доцент, кафедры АТ В.И. Семеновых

Синтез арифметико-логического устройства реализованного на элементах цифровой техники

Методические указания для курсового проекта по курсу "Автоматизация и оптимизация технологических процессов"

Составитель: кандидат технических наук, доцент кафедры ЭП и АПУ Е.Н.Малышев: Методические указания.- Киров: Издательство ВятГУ, 2008. –36 с.

Методические указания предназначены для студентов 3 курса дневной и заочной форм ускоренного обучения специальности 180400 «Электропривод и автоматика промышленных установок и технологических комплексов». Содержат методические указания для выполнения курсового проекта.

Компьютерная верстка и редактирование текста авторское

Текст напечатан с электронной версии, предоставленной автором

Подписано в печать Усл. печ.л. 1,8.

Бумага офсетная Печать матричная

Заказ № Тираж 50 Бесплатно

Текст напечатан с оригинал-макета, предоставленного составителем.

610000, г. Киров, ул. Московская, 36

© Вятский государственный университет, 2008

Цель курсового проекта – получить навыки синтеза арифметико-логического устройства, составления принципиальной схемы, разработки сборочного чертежа, трассировки печатной платы и выполнения чертежа детали – печатной платы.

Каждый студент получает индивидуальное именное задание, где перечислены входные сигналы, представлена таблица истинности для формирования выходного сигнала А, изображена циклограмма существования выходного сигнала В, словесно описаны условия появления и исчезновения выходного сигнала С. В задании так же указаны исполнительные устройства, срабатывающие при появлении выходных сигналов. Пример индивидуального задания приведен в приложении А.

1 Методические указания к выполнению пояснительной записки

Ниже даны пояснения к содержимому разделов пояснительной записки (ПЗ) далее в скобках указаны номера пунктов задания.

1.1 . В теоретической части (2.1.1) необходимо указать хотя бы следующие из основных параметров используемой серии логических элементов:

• Напряжение питания,

• Уровень логической единицы,

• Уровень логического нуля,

• Входной ток логической единицы

• Входной ток логического нуля

• Выходной ток логической единицы

• Выходной ток логического нуля

• Быстродействие (максимальная рабочая частота)

• Потребляемая мощность

К особенностям использования выбранной серии логических элементов (2.1.2) обычно относят следующее:

• Работа элемента при неподключенных входах.

• Возможность подключения к элементам других серий.

• Способы создания источников логической единицы и логического нуля.

• Помехоустойчивость

• Особенности подключения исполнительных устройств

Информацию о параметрах и особенностях использования выбранной серии необходимо изучить по справочной литературе [1…5].

1.2 При построении схемы для формирования сигнала А (2.2.1) необходимо из указанной в пункте 1.3 задания таблицы записать логическое выражение, на основе которого впоследствии строится функциональная и принципиальная схемы. Так как в задании требуется выполнить схему на минимальном количестве корпусов необходимо минимизировать (упростить) логическое выражение. Это удобнее сделать, используя карты Карно.

1.3 Карта Карно (диаграмма Вейча) – это более компактный способ представления таблицы истинности, в которой часть таблицы, где указывают возможные комбинации входных сигналов, отдельно не изображается. Здесь входная комбинация определяется расположением клетки (ячейки) в карте.

1.3.1 Правила составления каты следующие.

• Внутри клетки записывается состояние выходного сигнала при соответствующей расположению клетки комбинации. Таким образом, количество клеток в карте равно количеству комбинаций входных сигналов, которое в свою очередь зависит от количества входных сигналов и равно 2ⁿ, где n – число входных сигналов (аргументов логической функции). Так при двух входных сигналах количество входных комбинаций, а следовательно, и клеток в карте 4, при трех – 8, при четырех -16 и т.д.

• Карта должна быть прямоугольной.

• В половине клеток аргумент равен единице, в другой половине – нулю. При переходе из одной клетки в соседнюю должен менять свое значение только один аргумент. Соседними являются так же крайние левые клетки – крайним правым, крайние верхние – крайним нижним. Значение аргумента изображается вне карты четой, напротив черты аргумент равен 1.

С учетом указанных правил, для логической функции, таблица истинности которой задана в таблице 1, карта Карно примет вид изображенный на рисунке 1, для таблицы 2 – на рисунке 2.

Таблица 1 – таблица истинности выходного сигнала Х

Вход а	0	1	0	1	0	1	0	1
Вход в	0	0	1	1	0	0	1	1
Вход с	0	0	0	0	1	1	1	1
Выход Х	0	0	0	1	0	1	1	1

Рисунок 1 – Карта Карно для сигнала Х

Таблица 2 – таблица истинности выходного сигнала Y

Вход а	0	1	0	1	0	1	0	1	0	1	0	1	0	1	0	1
Вход в	0	0	1	1	0	0	1	1	0	0	1	1	0	0	1	1
Вход с	0	0	0	0	1	1	1	1	0	0	0	0	1	1	1	1
Вход d	0	0	0	0	0	0	0	0	1	1	1	1	1	1	1	1
Выход У	1	1	1	1	0	1	0	1	0	1	0	1	1	1	0	1

Рисунок 2 Карта Карно для сигнала Y

1.3.2 Для получения минимального выражения по карте Карно по 1 или по 0 соседние клетки объединяют в контура, и для каждого контура записывают элементарное произведение (по 1) или элементарную сумму (по 0). Контуров должно быть как можно меньше, а каждый контур – как можно больше. Контура должны быть прямоугольными и содержать 2^k клеток (k- целое число). Контура могут пересекаться, каждый новый контур должен охватывать хотя бы одну клетку, не принадлежащую другим контурам.

Если контура создавались по 1, то для каждого контура записывают элементарное логическое произведение, причем если контур пересекает границу аргумента, то в произведении этот аргумент отсутствует, если аргумент в контуре равен 0, то в произведении - аргумент с инверсией. Элементарные произведения объединяются логической суммой.

Если контура составлялись по 0, то для каждого контура записывают элементарное логическую сумму, причем если граница аргумента пересекается контуром, то в сумме он отсутствует, если аргумент в контуре равен 1, то в произведении - аргумент с инверсией. Логические суммы объединяются логическим произведением.

Если в карте есть клетки, состояние функций в которых не определено (не может быть по технологическому процессу), то в эту клетку можно установить такое состояние (0 или 1), которое позволит получить наименьшее количество контуров, охватывающих наибольшее количество клеток. В задании по курсовому проекту такие ситуации обозначены символом х.

Для рассмотренных выше (см. рисунки 1 и 2) сигналов X и Y контура для получения минимального логического выражения представлены на рисунках 3 и 4, а полученные логические выражения примут вид:

.

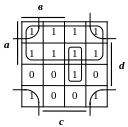
Рисунок 3 Рисунок 4

1.4 При создании функциональной схемы (2.2.2), а в дальнейшем и принципиальной(2.2.3), рекомендуется использовать базовые элементы типа И-НЕ, что позволяет уменьшить количество корпусов микросхем. Для этого предлагается использовать законы Де Моргана (инверсия суммы равна произведению инверсий и наоборот).

Преобразование рассматриваемых сигналов Х и Y приведено ниже

С учетом последнего выражения схема для сигнала Y примет вид изображенный на рисунке 5

Рисунок 5

1.5 При построении принципиальной схемы (2.2.3) необходимо учитывать последнее предложение пункта 1.2 задания – (при ненажатой кнопке входная ситуация воспринимается как логический ноль). Подробнее об этом читай в разделе 1.7.

1.6 При построении схемы для формирования сигнала В (2.2.4) возможно использование следующей инженерной методики