Тема 3. Піраміда, її властивості. Правильна, зрізана піраміда. Площа бічної поверхні правильної піраміди. Властивості паралельних перерізів у піраміді

План

1. Піраміда, її властивості.

2. Правильна, зрізана піраміда.

3. Площа бічної поверхні правильної піраміди.

1. Пірамідою називається многогранник, який полягає з площини многокутника - основи піраміди, точки, яка не лежить у площині основи,— вершини піраміди і всіх відрізків, що сполучають вершину піраміди з точками основи (мал. 14).

Відрізки, що сполучають вершину піраміди з вершинами

о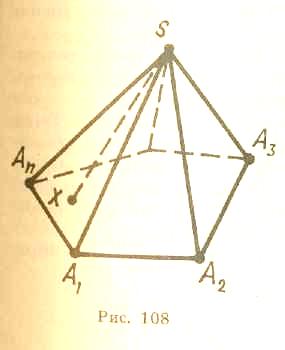 снови, називаються бічними ребрами.

Поверхня піраміди складається з основи і бічних граней. Кожна бічна грань — трикутник. Однією з його вершин є вершина піраміди, а протилежною стороною - сторона основи піраміди.

Висотою піраміди називається перпендикуляр, опущений з вершини піраміди на площину основи.

Піраміда називається n-кутною, якщо її основою - n-кутною. Трикутна піраміда називається також тетраедром.

Мал. 14

У піраміди, зображеної на малюнку 14, основа - багатокутник А₁А₂ ... А_n, вершина піраміди — S, бічні ребра SA₁, SА_2,, ... , SА_п - бічні грані — ∆SA₁A₂, ∆SА₂А₃, ... .

Надалі будемо розглядати тільки піраміди з опуклим багатокутником в основі. Такі піраміди є опуклими многогранниками.

Відповідно до правил паралельного проектування піраміду зображують таким чином. Спочатку будують основу. Це — деякий плоский многокутник. Потім позначають вершину піраміди, яку з'єднують бічними ребрами з вершинами основи. На малюнку 14 зображена п’ятикутна піраміда.

Перерізами піраміди площинами, які проходять через її вершину, є трикутники (мал. 15). Зокрема, трикутниками є діагональні перерізи. Це перерізи площинами, які проходять через два не сусідніх бічних ребра піраміди (мал. 16).

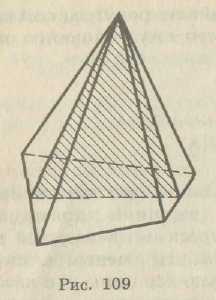
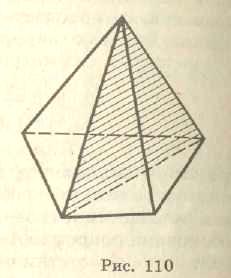
Мал.15 Мал. 16

Щоб побудувати переріз піраміди площиною, досить побудувати переріз її бічних граней із січною площиною.

Якщо на грані, не паралельній сліду g (пряма, яка лежить у площині основи), відома яка-небудь точка А, що належить перерізу, то спочатку будують перетин сліду січної площини з площиною цієї грані — точку D на малюнку 17. Точку D сполучають з точкою А прямою. Тоді відрізок цієї прямої, який належить грані, є перетином цієї грані із січною площиною. Якщо точка А лежить на грані, паралельній сліду g, то січна площина перетинає цю грань по відрізку, паралельному прямій g. Перейшовши до сусідньої бічної грані, будують її перетин із січною площиною і т.д. В результаті дістають шуканий переріз піраміди.

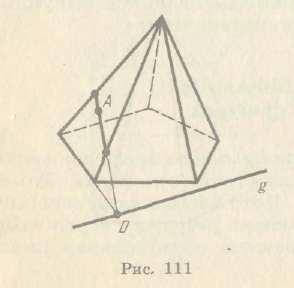
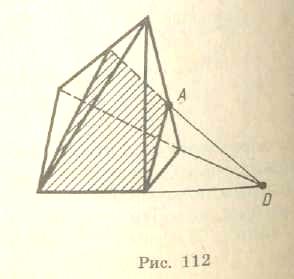
Мал. 17 Мал.18

На малюнку 18 побудовано переріз чотирикутної піраміди площиною, яка проходить через сторону основи і точку А на одному з її бічних ребер.

2. Піраміда називається правильною, якщо її основою є правильний многокутник, а основа висоти збігається з центром цього многокутника. Віссю правильної піраміди називається пряма, яка містить її висоту. Очевидно, у правильній піраміді бічні ребра рівні, отже, бічні грані — рівні рівнобедрені трикутники.

Висота бічної грані правильної піраміди, проведена з її вершини, називається апофемою.

Теорема 5. Площину, яка перетинає піраміду і паралельна її основі, відтинає подібну піраміду.

Д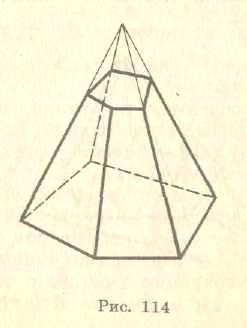 руга частина піраміди — це многогранник, який називається зрізаною пірамідою (мал. 19). Грані зрізаної піраміди, що лежать у паралельних площинах, називаються основами; інші грані називаються бічними гранями. Основи зрізаної піраміди є подібні ( більше того, гомотетичні) многокутники, бічні грані — трапеції.

Зрізана піраміда, яка отримана з правильної, також називається правильною. Бічні грані правильної зрізаної піраміди — рівні рівнобокі трапеції; їхні висоти називаються апофемами.

Мал.19

3. Бічною поверхнею піраміди називається сума площ її бічних граней.

Теорема 6. Бічна поверхня правильної піраміди дорівнює добутку півпериметра основи на апофему.

Доведення. Якщо сторона основи а, а кількість сторін п, то бічна поверхня піраміди дорівнює:

· n = = ,

де l — апофема, а р — периметр основи. Теорема доведена.