Тема 1. Лінійний кут двогранного кута. Поняття про многогранний кут. Многогранники. Призма. Правильна призма. Площа бічної поверхні правильної призми

План

1. Лінійний кут двогранного кута. Поняття про многогранний кут.

2. Многогранники.

3. Призма.

4. Правильна призма.

5. Площа бічної поверхні правильної призми

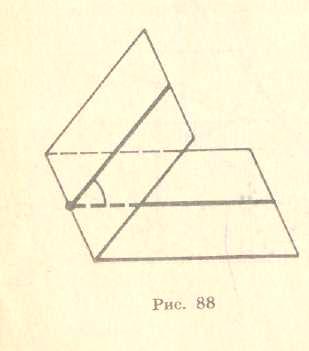1.Двогранним кутом називається фігура, утворена двома півплощинами із спільною прямою, що їх обмежує (мал. 1). Півплощини називаються гранями, а пряма, що обмежує їх,— ребром двогранного кута.

Площина, перпендикулярна до ребра двогранного кута, перетинає його грані по двох напівпрямих. Кут, утворений цими напівпрямими, називається лінійним кутом двогранного кута. За міру двогранного кута приймається міра відповідного йому лінійного кута. Усі лінійні кути двогранного кута суміщаються паралельним перенесенням, а отже, вони рівні. Тому міра двогранного кута не залежить від вибору лінійного кута.

Мал.1

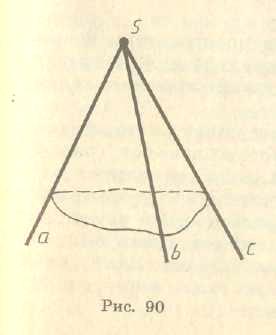
Розглянемо три промені а, b, с, які виходять з однієї точки і не лежать в одній площині. Тригранним кутом (аbс) називається фігура, яка складається з трьох плоских кутів (аb), (bс) і (ас) (Мал. 2). Ці кути називаються гранями тригранного кута, а їх сторони — ребрами. Спільна вершина плоских кутів називається вершиною тригранного кута.

Двогранні кути, утворені гранями тригранного кута, називаються двогранними кутами тригранного кута.

Аналогічно дають означення многогранного кута (a₁а₂а₃…а_n) - як фігури, яка складається з плоских кутів (а₁а₂), (а₂а₃), (а₃а₄), …, (а_nа₁). (рис. 3). Для многогранного кута визначаються поняття граней, ребер і двогранних кутів так само, як і для тригранного кута.

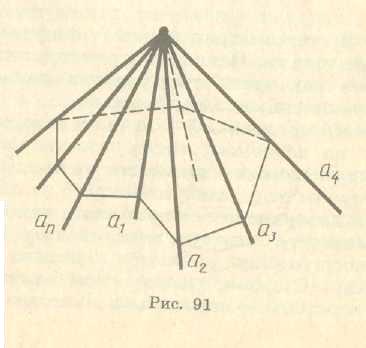
Мал.2 Мал.3

2. У стереометрії вивчають фігури у просторі, які називаються тілами.

Многогранник — це таке тіло, поверхня якого складається із скінченної кількості плоских багатокутників (мал. 4). Многогранник називається опуклим, якщо він лежить по один бік від площини кожного з плоских многокутників на його поверхні. Спільна частина такої площини і поверхні опуклого многогранника називається гранню. Грані опуклого многогранника є плоскими опуклими многокутниками. Сторони граней називаються ребрами многогранника, а вершини — вершинами многогранника.

Мал.4 Мал.5

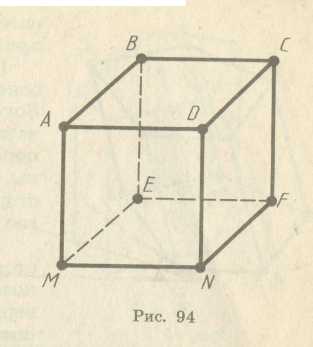
Пояснимо сказане на прикладі відомого вам куба (мал. 5). Куб — це опуклий многогранник. Його поверхня складається з шести квадратів АВСD, ВЕFС, ... . Вони є його гранями. Ребрами куба є сторони цих квадратів АВ, ВС, ВЕ, ... . Вершинами куба є вершини квадратів А, В, С, D, Е... . Куб має шість граней, дванадцять ребер і вісім вершин.

Найпростішим многогранникам — призмам і пірамідам, які будуть основним об'єктом нашого вивчення, ми дамо такі визначення, в яких по суті не використовується поняття тіла. Означимо їх як геометричні фігури з переліком усіх точок простору, які їм належать.

3.Призмою називається многогранник, який складається з двох плоских многокутників, які лежать у різних площинах і суміщаються паралельним перенесенням, та всіх відрізків, що сполучають відповідні точки цих многокутників (мал. 6).

Многокутники називаються основами призми, а відрізки, які сполучають відповідні вершини,— бічними ребрами призми.

Оскільки паралельне перенесення є рух, то основи призми рівні.

Через те, що при паралельному перенесенні площина переходить у паралельну площину (або в себе), то основи призми лежать у паралельних площинах.

Оскільки при паралельному перенесенні точки зміщуються вздовж паралельних прямих або прямих, які збігаються, на одну і ту саму відстань, то бічні ребра призми паралельні і рівні.

Мал.6

Поверхня призми складається з основ і бічної поверхні. Бічна поверхня складається з паралелограмів. Кожен з цих паралелограмів має дві сторони, які є відповідними сторонами основи а дві інші — суміжними бічними ребрами.

Висотою призми називається відстань між площинами її основ.

Відрізок, який сполучає дві вершини призми, що не належать одній грані, називається діагоналлю призми.

Призма називається n-кутною, якщо її основи - n-кутники. Надалі ми будемо розглядати тільки призми, у яких основи — опуклі многокутники. Такі призми є опуклими многогранниками. На малюнку 6 зображено п’ятикутну призму. Основи її є п'ятикутники А₁А₂А₃А₄А₅, А'₁А'₂А'₃А'₄А'₅. XX' - відрізок, який сполучає відповідні точки основ. Бічні ребра призми – відрізки А₁А'₁, А₂А'₂,, …, А₅А'₅.. Бічні грані призми – паралелограми А₁А₂А'₂А₁, А₂А₃А'₃А'₂, ….

П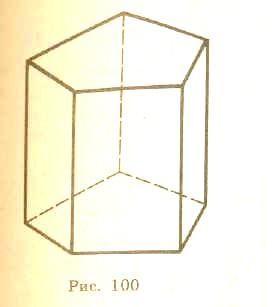 ризма називається прямою, якщо її бічні ребра перпендикулярні до основ. У противному разі призма називається похилою.

Бічні грані прямої призми прямокутники. Зображуючи пряму призму на рисунку, бічні ребра звичайно проводять вертикально (мал. 7).

Пряма призма називається правильною, якщо її основи - правильні многокутники.

4.Площею бічної поверхні призми називається сума площ бічних граней. Повна поверхня призми дорівнює сумі бічної поверхні і площ основ.

Мал. 7

Теорема 1. Бічна поверхня прямої призми дорівнює добутку периметра основи на висоту призми, тобто на довжину бічного ребра.

Доведення. Бічні грані прямої призми — прямокутники. Основи цих прямокутників є сторонами многокутника, що лежить в основі призми, а висоти дорівнюють довжині бічних ребер. Звідси випливає, що бічна поверхня призми дорівнює:

S =а₁ℓ + а₂ℓ + ... а_пℓ = рℓ,

де а₁, ... , а_п — довжини ребер основи, р — периметр основи призми, а ℓ — довжина бічних ребер. Теорема доведена.