4. Ряд фибоначчи и бинарный ряд

       Возьмем теперь, в качестве логических пар целостную пару <2,2>. Эта пара будет характеризовать количественный состав  первой логической оболочки. Тогда,  в процессе ее "крещения" у нас произведется следующая бинарная пара <4,4>. Эта пара по своей структуре будет характеризовать звездный тетраэдр (или куб), имеющий восемь вершин. Мы получили первую подоболочку второго периода.  Удвоение этих подоболочек даст пару <8,8>, эволюция которой приведет к паре <16,16>, а далее к паре <32,32>.

        Соединяя полученные бинарные пары в единую цепочку, мы получаем ряд

<2, 8,16,32>. Именно такая последовательность характеризует количественный состав оболочек Периодической системы химических элементов.

    Таким образом, единство ряда Фибоначчи и бинарного ряда является неоспоримым фактом. Периодическая система химических элементов, бинарный ряд, ряд Фибоначчи и золотое сечение оказываются тесно взаимосвязанными.

                     

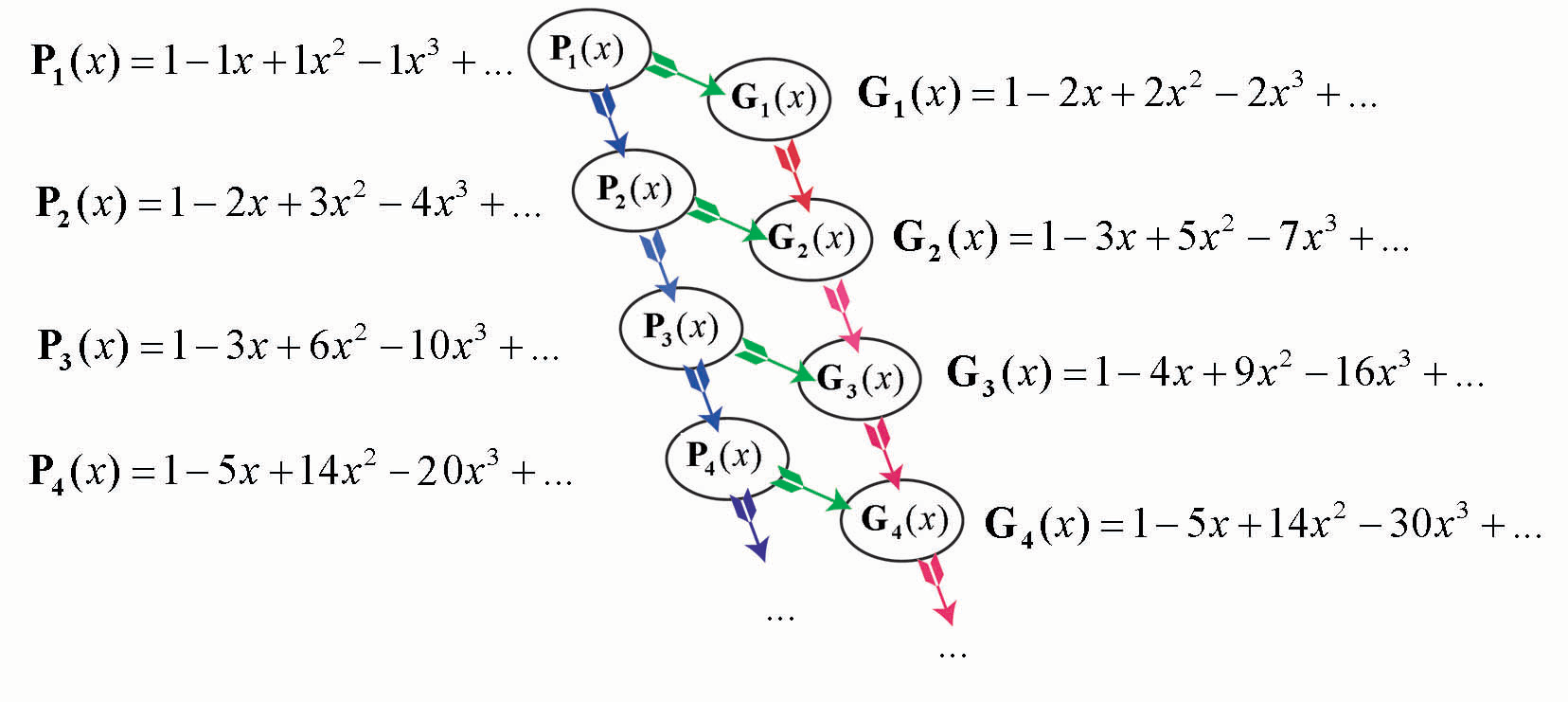
                                                                                           Рис. 6

        Из последней схемы видно, что производящие функции этих рядов еще и тесно взаимосвязаны с биномом Ньютона (1-х) ^-n.

        Между рядом Фибоначчи и бинарным рядом также существует прямая связь (рис. 4)

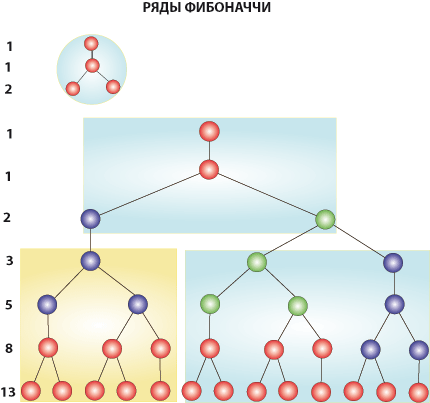
рис. 7-1

            На этом рисунке видно, как из исходного соотношения (1-1-2), используя бинарный ряд,  выстраивается весь ряд Фибоначчи. Эту схему приводит в своей книге Д. Мельхиседек ("Древняя тайна  Цветка Жизни", том. 2, стр.283). Этот рисунок  показывает  семейное дерево трутня пчелы. 

Но что-же лежит в основе ряда Фибоначчи, что лежит в его Замысле? На этот вопрос дает ответ следующий рисунок

                                      

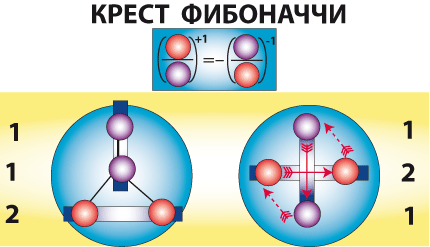
рис. 7-2

Из этого рисунка видно, что ряд Фибоначчи порождается рычажными весами, в результате  обхода по кресту.

Из рисунков 7-1 и 7-2 видна многоуровневость и многомерность ряда Фибоначчи:

Каждый член ряда Фибоначчи способен к формированию и формирует, по образу и подобию, собственный ряд Фибоначчи.

    Мельхиседек подчеркивает, что  ряд Фибоначчи (1-1-2-3-5-8-13-...) является женским рядом, в то время как бинарный ряд  (1-2-4-8-16-32-...) является мужским. И эти свойства  в полной мере проявляются в свойствах чисел Русской матрицы (Русская матрица- 1), утверждающих, что

                                             "ВСЕ ЕСТЬ ЧИСЛО РУССКОЙ МАТРИЦЫ"

       В этой матрице каждое число двойственное. И все они порождены бинарной (мужской) и золотосеченной (женской)  производящими функциями.

       Из последнего рисунка можно осознать, что последовательность <1,1,2> и <1,2,1>  являются взаимодополнительными, как оболочки и подоболочки Периодической системы химических элементов (Атом-3).

                                                 

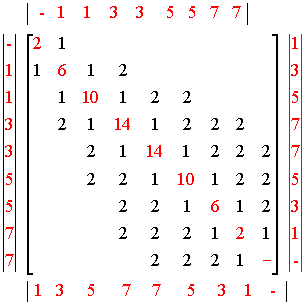
Данная матрица представляет собой проекцию многомерного кристалла Периодической системы химических элементов на плоскость. По этой проекции "плоскарик" (двумерное существо, живущее в двумерном пространстве) может не только представить себе многомерный мир Периодической системы химических элементов, но и сформировать этот многомерный кристалл, в котором подоболочки

(1(1,2(1,2,2(1,2,2,2))))   сплетаются в   подоболочки   (1(1,3(1,3,5(1,3,5,7)))), формируя ряд Фибоначчи.

И заметьте, что проекция пространственного кристалла на вектор-горизонталь формирует последовательность многомерных подоболочек <1,1, 3,3,5,5,7,7>.

Другая проекция ортогональная первой, формирует последовательность <1,3,5,7,7,5,3,1>

Остается только удивляться почему ученые недооценили свойства этой матрицы. Они заметили только интегральный результат трансформации базисных подоболочек.