
- •Раскройте назначение и состав радиоствола.
- •Приведите структурную схему ствола двусторонней радиосистемы передачи.
- •Опишите структурную схему ретранслятора.
- •Дайте характеристику и план распределения частот в дуплексном стволе радиосистемы передачи.
- •Назовите причины искажений сигналов в радиосистемах передачи.
- •Дайте определение канала передачи радиосигналов и опишите его общую структуру.
- •Опишите состав радиотракта канала передачи.
- •Раскройте содержание энергетического бюджета канала связи.
- •Приведите классификацию радиосистем передачи по принадлежности к различным службам и по назначению.
- •Назовите диапазоны используемых радиочастот или радиоволн при построении радиосистем передачи.
- •Приведите классификацию радиосистем по виду передаваемых сигналов и способу разделения каналов.
- •Приведите классификацию радиосистем по виду модуляции несущей.
- •Раскройте классификацию систем по пропускной способности.
- •В чем заключается особенность пропускной способности спутниковых систем передачи.
- •Приведите классификацию радиосистем передачи по характеру используемого физического процесса в тракте распространения радиоволн.
- •Какой радиоканал называется идеальным каналом, и какие его особенности?
- •Охарактеризуйте параметры телекоммуникационных каналов.
- •Дайте определения основных параметров качественных телекоммуникационных каналов и систем.
- •Чем определяется пропускная способность канала связи?
- •Поясните содержание и график фундаментальной границы Шеннона.
- •Проведите сравнительную характеристику спектральной эффективности различных типов цифровой модуляции, используемых в радиорелейных и спутниковых системах передачи.
- •Назовите и поясните критерии помехоустойчивости телекоммуникационных каналов фиксированной связи.
- •Дайте характеристику критериев помехоустойчивости спутниковых цифровых систем передачи вещания стандарта dvb-s.
- •Назовите и поясните критерии помехоустойчивости аналого-цифровых радиорелейных систем передачи.
- •Дайте характеристику надежности функционирования канала связи.
- •В чем отличие в определении надежности для телекоммуникационных систем без ремонта (восстановления) и с возможностью их восстановления.
- •Ответы:
- •4.3.2. Рефракционные замирания интерференционного типа
- •4.3.3. Интерференционные замирания из-за отражений
- •4.3.4. Замирания из-за экранирующего влияния слоистых неоднородностей тропосферы
- •Замирания из-за влияния диаграммы направленности антенн. Потери усиления антенн.
- •Замирания из-за ослабления сигнала гидрометеорами. Ослабление сигнала в дожде, снеге, граде, в туманах и облаках.
- •4.4.6.1. Ослабления сигнала в дожде
- •Ослабления в дожде
- •Для сухого снега и дождя
- •Эффективная длина трассы.
- •Замирания из-за поглощения в горах, в песчаных и пыльных бурях.
- •При вертикальной поляризации
- •Профиль, просвет и классификация трасс.
- •Медленные и быстрые замирания.
- •Интерференционные формулы для расчета множителя ослабления.
- •Коэффициент отражения от земной поверхности.
- •Частотная селективность множителя ослабления.
- •Общие положения при распределении радиочастотного ресурса для использования радиорелейными системами передачи.
- •Планы частот радиорелейных станций. . Планы частот радиорелейных станций
- •Влияние кросс-поляризационной избирательности и частотной избирательности фильтров на выбор плана частот.
- •Формулы расчета рабочих частот радиорелейных станций.
Медленные и быстрые замирания.
Медленные и быстрые замирания
Медленные замирания сигналов
Медленные замирания сигналов обусловлены изменением условий рефракции радиоволн, а также перемещением мобильных пользователей на расстояния, превышающие длину волны на несколько порядков и более.
Медленные
замирания сигналов моделируются
логарифмическим законом распределения
мгновенных значений огибающей принимаемого
сигнала
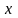 с плотностью
с плотностью
 :
:
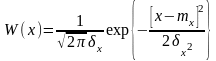 ,
где
,
где
 - математическое
ожидание (среднее значение сигнала х);
- математическое
ожидание (среднее значение сигнала х);
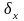 - дисперсия замирания
сигнала (среднее квадратическое
отклонение от среднего значения сигнала
х).
- дисперсия замирания
сигнала (среднее квадратическое
отклонение от среднего значения сигнала
х).
Быстрые замирания сигналов
Причиной быстрых замираний является многолучевость распространения радиоволн и передвижение пользователей на кроткие расстояния, сравнимые с длиной волны.
Максимальная глубина быстрых замираний в пределах полного интервала многолучевого расстояния (полное время запаздывания последнего импульса относительно первого) может достигать 20 30 дБ, а интервал корреляции – доли, единицы секунд.
При наличии преобладающего по амплитуде прямого незамирающего луча распределение мгновенных значений огибающей сигнала аппроксимируется законом Рэлея-Райса:

 ,
,
где
 - модифицированная функция Бесселя
нулевого порядка первого рода;
- модифицированная функция Бесселя
нулевого порядка первого рода;
 - параметр,
характеризующий отношение энергии
прямого луча к суммарной энергии
рассеянных сигналов.
- параметр,
характеризующий отношение энергии
прямого луча к суммарной энергии
рассеянных сигналов.
В
случае, когда точка доступа находится
вне зоны прямой видимости (прямой луч
отсутствует и на входе приемника есть
только рассеянные компоненты сигнала,
 ),
распределение Рэлея-Райса сводится к
распределению Рэлея:
),
распределение Рэлея-Райса сводится к
распределению Рэлея:
 ,
.
,
.
Интерференционные формулы для расчета множителя ослабления.
Интерференционные формулы для расчета множителя ослабления
Модуль множителя ослабления V рассчитывается по интерференционным формулам. При наличии q точек отражения
 ,
(4.19)
,
(4.19)
i = 1,2,…,q.
При одной отраженной волне
 ,
(4.20)
,
(4.20)
где Φ–модуль коэффициента отражения от земной поверхности, зависящий от характера рельефа местности и угла скольжения ,
= H(g)/2R0k(1 - k);
H(g) – просвет на трассе с учетом рефракции; k – относительная координата точки отражения; – сдвиг фаз между интерферирующими волнами:
= (2/)r + = + ; (4.21)
r – разность хода между интерферирующими волнами:
r = H2(g)/2R0k(1 - k); (4.22)
– фаза коэффициента отражения.
Значение просвета Н(g) при изменении условий рефракции вычисляется по формуле:
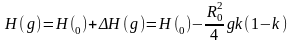 ,
где
,
где
 - значение просвета при отсутствии
рефракции, определяемое из профиля
интервала.
- значение просвета при отсутствии
рефракции, определяемое из профиля
интервала.
Приращение
просвета
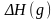 при
данном значении g
равно:
при
данном значении g
равно:

Везде,
где есть g, следует иметь ввиду gэфф.
Как следует из этой формулы, при изменении
g существенно меняется приращение
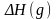 и соответственно реальный просвет
и соответственно реальный просвет
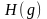 по сравнению с
по сравнению с
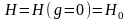 при отсутствии рефракции.
при отсутствии рефракции.
Причем изменяется следующим образом:
При
 (т.е. при положительной рефракции)
(т.е. при положительной рефракции)
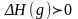 и, следовательно, реальный просвет
на трассе увеличивается по сравнению
с
и, следовательно, реальный просвет
на трассе увеличивается по сравнению
с
 .
.При
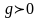 (т.е. при субрефракции)
(т.е. при субрефракции)
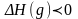 и, следовательно, реальный просвет на
трассе уменьшается по сравнению с
.
и, следовательно, реальный просвет на
трассе уменьшается по сравнению с
.
При
этом наиболее сильно просвет изменяется
в середине трассы
 .
.
Из этого следует, что определяющим методом борьбы с субрефракцией является правильный выбор высот подвеса антенн на этапе проектирования. А правильный выбор высот подвеса в значительной степени зависит от точности построения профиля интервала.
При малых углах , что мы имеем в случае трасс радиорелейных линий, и тогда
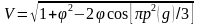 ,
(4.23)
,
(4.23)
где р(g) – относительный просвет на трассе при заданном значении g
р(g) = H(g)/H0 = [H(о) + H(g)]/H0; (4.24)
При p(g)=l, что соответствует Η(g)= Η0 и r=/6 имеем V = l, если Ф = 0 или Ф = 1; V 1, если 0<Ф<1; V = l±(0,10,15), если Φ = 0,30,7.
При р(g)>1 наблюдается интерференционная картина поля.
График зависимости V от p(g) приведен на рис. 4.13.

Рис. 4.13. Зависимость множителя ослабления V от величины относительного просвета на трассе p(g): 1 – ; 2 – =10; 3 –=5; 4 –=3; 5 –=2; 6 –=1,5; 7 –=1,2; 8 – =1,0; 9–=0,9; 10 – =0,8 11 –=0,7; 12 –=0,6; 13 –=0,5; 14 –=0,4; 15 – 0
Параметр , характеризующий (в некоторой степени) остроконечность или клиновидность препятствия, вычисляется по формуле:
 ,
,
где Н0 – величина критического просвета, где находится препятствие, с относительным расстоянием k, Rпр – радиус препятствия, R – расстояние связи на интервале.
При идеальном отражении радиоволн от поверхности земли, т.е. при Ф=1 (4.23) принимают вид
 (4.23а)
(4.23а)
Максимальные
значения множителя ослабления Vm
(интерференционные максимумы) наблюдаются
при условии
 .
.
В этом случае аргумент косинуса
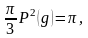 3π, 5π, …, (2 m-1)
π,
3π, 5π, …, (2 m-1)
π,
где m=1, 2, … номер интерференционного максимума.
Откуда
видно, что относительный просвет
 принимает максимальное значение:
принимает максимальное значение:
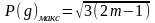 ,
(4.25)
,
(4.25)
В этом случае просветы H(g) соответствуют радиусам нечетных зон Френеля. Значение модуля множителя ослабления в m-м интерференционном максимуме
Vm = 1 + Фm , (4.26)
где Φm – модуль коэффициента отражения для m-го максимума.
Минимальные
значения множителя ослабления Vn
(интерференционные минимумы) наблюдаются
при условии
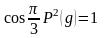 .
.
В этом случае аргумент косинуса
 4π; 6π; 2 n π,
4π; 6π; 2 n π,
где n=1, 2, … номер интерференционного минимума.
Откуда следует, что интерференционные минимумы наблюдаются при следующих значениях относительной величины просвета:
 ,
,
где n=1, 2, 3,...–номер минимума. В этом случае просветы H(g) соответствуют радиусам четных зон Френеля. Значение модуля множителя ослабления в n-м минимуме
Vn = 1 – Фn, (4.27)
где Фn – модуль коэффициента отражения для n-го минимума.
Значение Vn резко зависит от Фn, особенно при Фn1.
