
В иды проецирования. Центральное проецирование
В
Рис. 1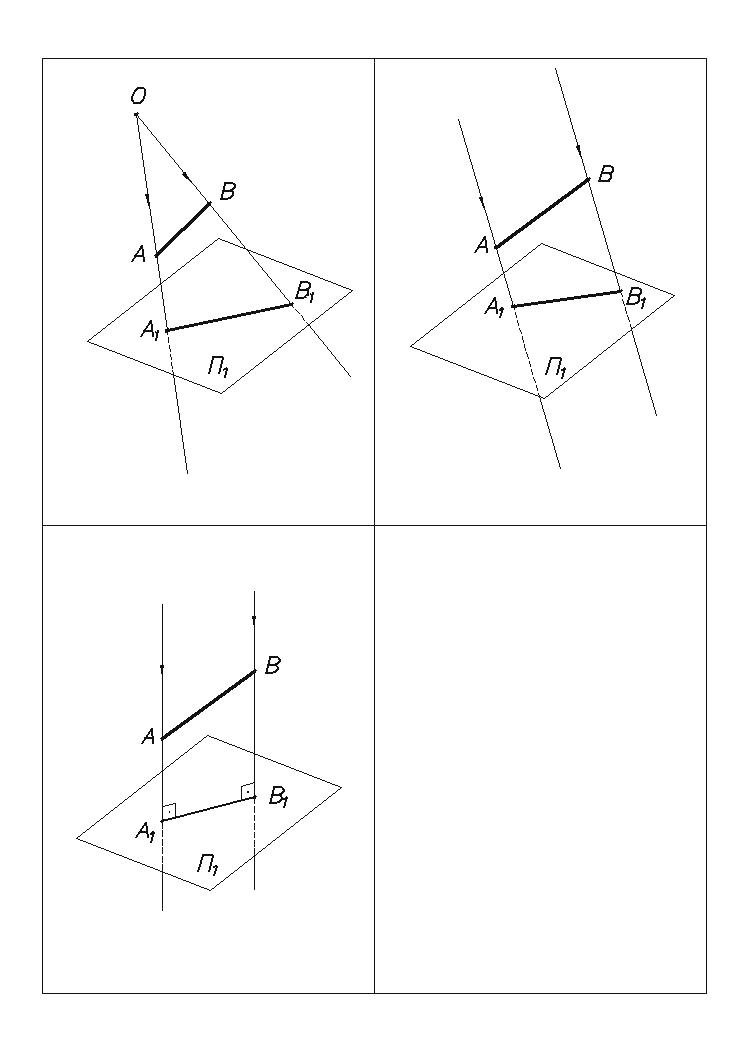
проецирования называется линейным центральным проецированием ( Л.Ц.П.)
Параллельное проецирование
Проецирование, при котором центр проекций удален в бесконечность, называется параллельным (Рис.2).При параллельном проецировании проецирующие прямые параллельны между собой. Угол наклона прямых к
Р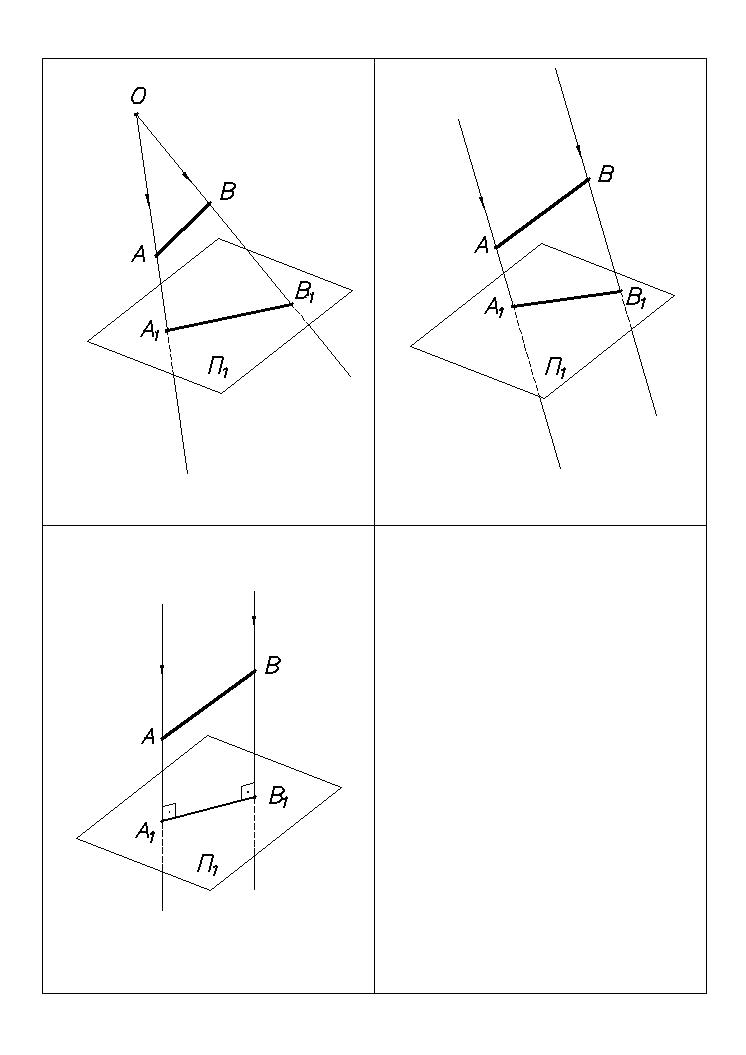 ис.2
плоскости П1
от 0 до 90 .
ис.2
плоскости П1
от 0 до 90 .
Ортогональное проецирование (частный случай параллельного проецирования).
В этом случае проецирующие прямые (Рис.3) перпендикулярны (ортогональны) плоскости проекций П1 (s П1). Этот вид проецирования и применяется при выполнении машиностроительных чертежей.
Рис.3
С войства
ортогонального проецирования.
войства
ортогонального проецирования.
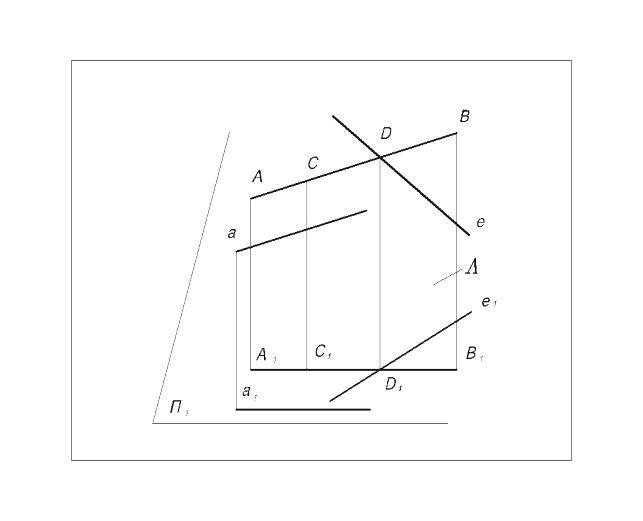
Позиционные свойства (Рис.4):
1. каждой точке проецируемого Г.О. соответствует одна точка на плоскости проекций, А А1;
2. проекцией прямой линии АВ является прямая линия А1В1, АВА1В1;
если точка принадлежит линии, то ее проекция принадлежит проекции данной линии, С АВ С1 А1В1;
4. проекцией точки пересечения двух прямых является точка пересечения проекций данных прямых; D = АВ х е D1 = А1 В1 х e1;
Рис.4 5. проекциями двух параллельных прямых являются две
 параллельные
прямые, а
II
AB
а1
II
А1
В1;
параллельные
прямые, а
II
AB
а1
II
А1
В1;
Метрические свойства (Рис.5)
1. При ортогональном проецировании величины отрезка прямой (АВ) и его проекции (А1 В1) связаны между собой соотношением А1 В1= АВ Соs , где - угол наклона прямой АВ к плоскости проекций П1.
2. При ортогональном проецировании отношения между отрезками прямой пропорциональны соответствующим отношениям между их проекциями (Рис.5).АС : СВ = А1С1 : C1B1
3. Теорема о проецировании прямого угла.
Рис.5 Если один из катетов прямого угла параллелен плоскости проекций, а второй не занимает проецирующего положения (не перпендикулярен плоскости проекций), то данный прямой угол на эту плоскость проекций проецируется без искажения.
Обратимость чертежа
Вышеприведенные чертежи называются однокартинными. Однокартинный чертеж не обладает свойством обратимости. Проекционный чертеж становится обратимым при добавлении дополнительной информации.
Рис.7
Рис. 6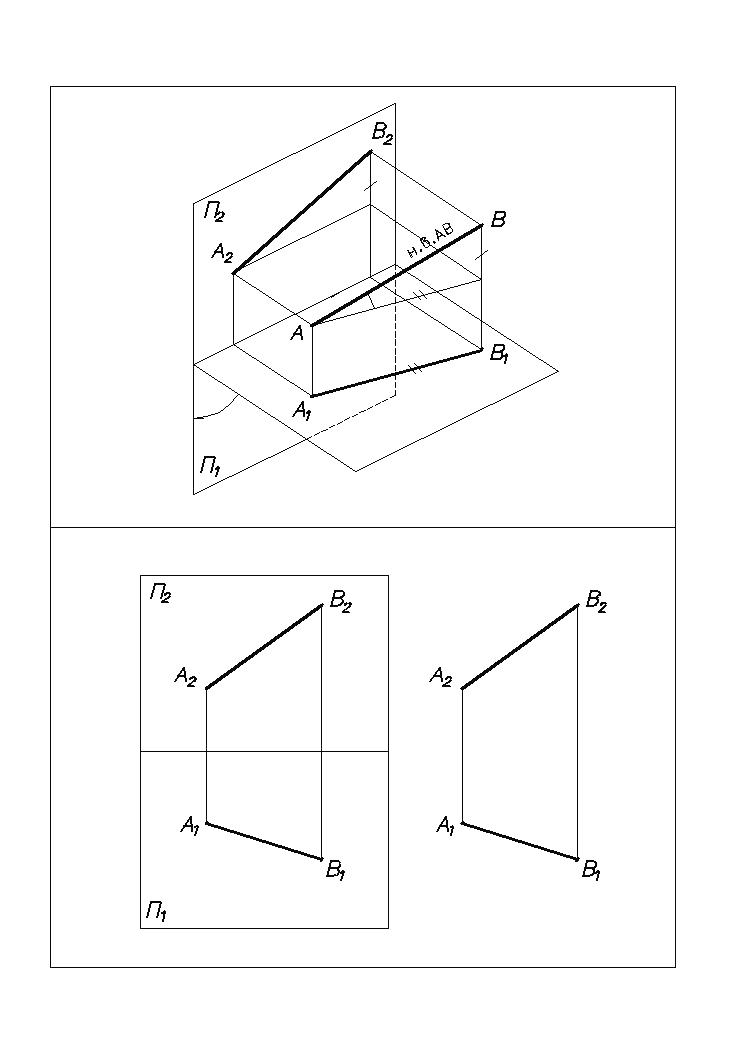
горизонтальная проекция точки А; А2 – фронтальная проекция точки А; А1А2 - линия связи. Если на К.Ч. заданы две проекции точки, точка однозначно задана на К.Ч.
Н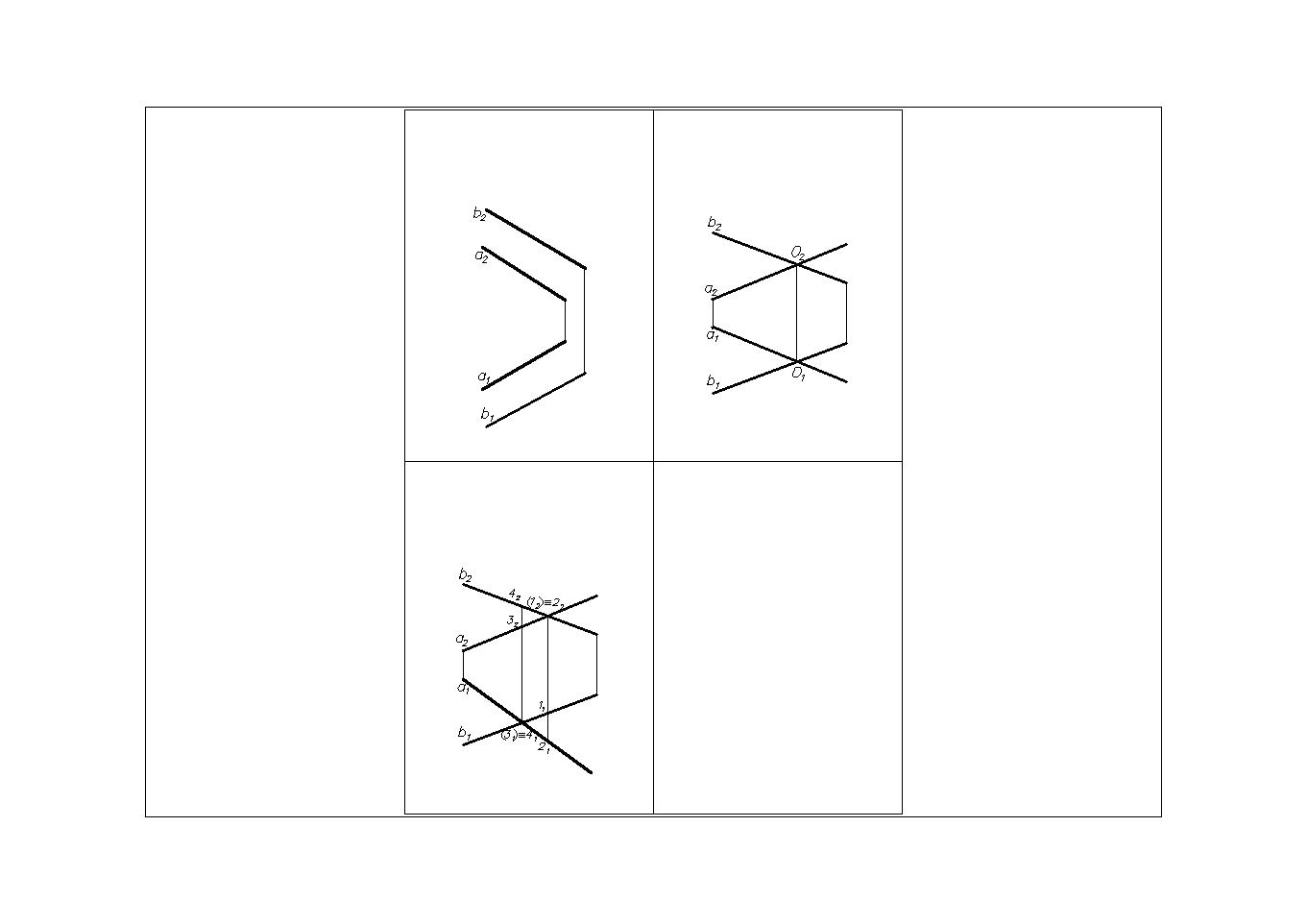 а
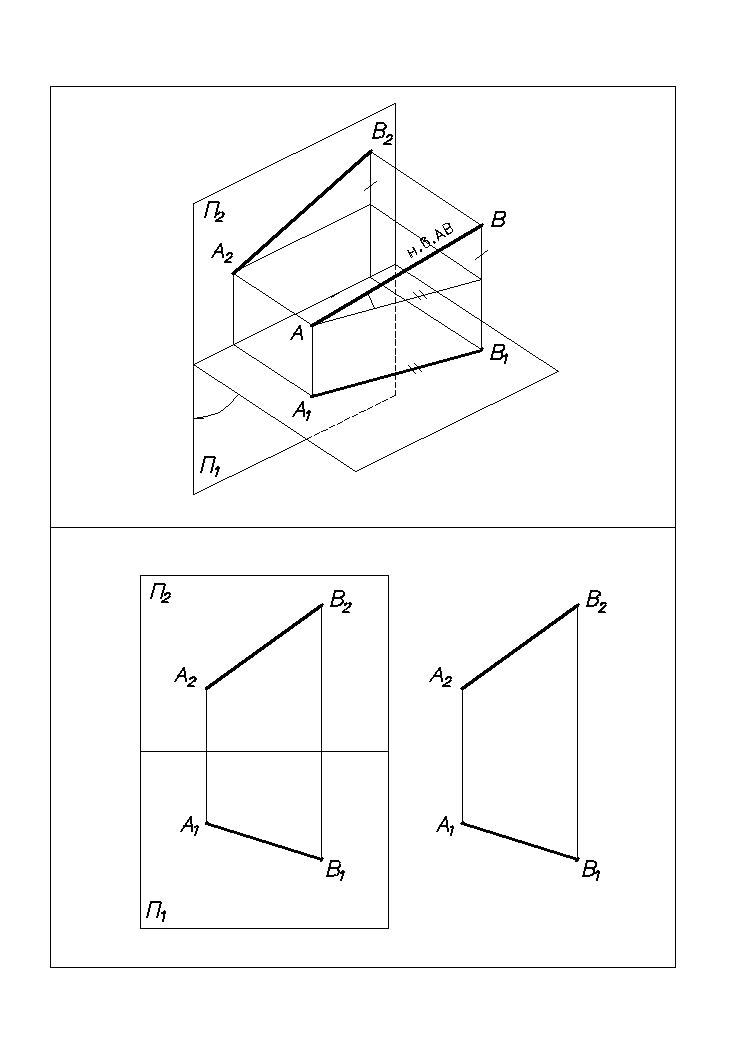
рис. 7 приведен комплексный чертеж
прямой АВ.
Прямая однозначно задана на комплексном
чертеже, если заданы две ее проекции.
а
рис. 7 приведен комплексный чертеж
прямой АВ.
Прямая однозначно задана на комплексном
чертеже, если заданы две ее проекции.
