Результаты измерений вертикальной неустойчивости
10 |
6 |
10 |
9 |
7 |
11 |
8 |
5 |
7 |
12 |
8 |
12 |
11 |
10 |
9 |
6 |
9 |
4 |
8 |
10 |
8 |
6 |
8 |
5 |
11 |
10 |
6 |
2 |
4 |
6 |
7 |
9 |
8 |
9 |
7 |
7 |
9 |
15 |
2 |
8 |
7 |
6 |
7 |
4 |
6 |
7 |
4 |
13 |
10 |
9 |
12 |
10 |
9 |
12 |
14 |
8 |
9 |
12 |
14 |
10 |
8 |
8 |
9 |
7 |
6 |
7 |
9 |
10 |
6 |
9 |
5 |
5 |
6 |
10 |
10 |
10 |
6 |
7 |
8 |
6 |
10 |
2 |
9 |
8 |
6 |
4 |
10 |
10 |
9 |
12 |
1. Рассчитываем частости по формуле
2.Рассчитывают среднее арифметическое значение (1.1)
3. Вычисляют среднеквадратическое значение (1.3)
4. Далее для расчета критериев согласия по интервалам и суммарного критерия согласия составляют и заполняют табл. 1.9.
r |
xi |
mi |
pi |
mi*xi |
|
|
1 |
2 |
3 |
0,033333 |
6 |
|
114,4948 |
2 |
3 |
0 |
0 |
0 |
|
0 |
3 |
4 |
5 |
0,055556 |
20 |
|
87,26914 |
4 |
5 |
4 |
0,044444 |
20 |
|
40,39309 |
5 |
6 |
13 |
0,144444 |
78 |
|
61,65531 |
6 |
7 |
11 |
0,122222 |
77 |
|
15,25877 |
7 |
8 |
11 |
0,122222 |
88 |
|
0,347654 |
8 |
9 |
14 |
0,155556 |
126 |
|
9,464691 |
9 |
10 |
16 |
0,177778 |
160 |
|
53,1279 |
10 |
11 |
3 |
0,033333 |
33 |
|
23,89481 |
11 |
12 |
6 |
0,066667 |
72 |
|
87,6563 |
12 |
13 |
1 |
0,011111 |
13 |
|
23,25383 |
13 |
14 |
2 |
0,022222 |
28 |
|
67,79654 |
14 |
15 |
1 |
0,011111 |
15 |
|
46,54272 |
|
|
|
Xcрa= |
8,177778 |
|
7,01284 |
n= |
90 |
|
Xcpk= |
2,648177 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k= |
5 |
|
|
|
|
|
xi-Xcpa |
t |
p(t) |
p(xi) |
nPi |
xi^2 |
|
P1 |
q |
|
-6,17778 |
-2,33284 |
0,0264 |
0,009969 |
0,897221 |
4,928193 |
|
0,009969 |
0,990031 |
|
-5,17778 |
-1,95522 |
0,0596 |
0,022506 |
2,025545 |
|
|
0,022506 |
0,977494 |
|
-4,17778 |
-1,57761 |
0,1145 |
0,043237 |
3,891357 |
0,315851 |
|
0,043237 |
0,956763 |
|
-3,17778 |
-1,19999 |
0,1942 |
0,073333 |
6,600013 |
|
|
0,073333 |
0,926667 |
|
-2,17778 |
-0,82237 |
0,285 |
0,107621 |
9,68591 |
1,133935 |
|
0,107621 |
0,892379 |
|
-1,17778 |
-0,44475 |
0,3621 |
0,136736 |
12,3062 |
0,138643 |
|
0,136736 |
0,863264 |
|
-0,17778 |
-0,06713 |
0,3982 |
0,150368 |
13,53309 |
0,474136 |
|
0,150368 |
0,849632 |
7,289 |
0,822222 |
0,310486 |
0,3814 |
0,144024 |
12,96213 |
0,083102 |
|
0,144024 |
0,855976 |
|
1,822222 |
0,688104 |
0,3166 |
0,119554 |
10,75986 |
2,551996 |
|
0,119554 |
0,880446 |
|
2,822222 |
1,065723 |
0,3939 |
0,148744 |
13,38695 |
|
|
0,148744 |
0,851256 |
|
3,822222 |
1,443341 |
0,3621 |
0,136736 |
12,3062 |
3,231557 |
|
0,136736 |
0,863264 |
|
4,822222 |
1,820959 |
0,0761 |
0,028737 |
2,586308 |
|
|
0,028737 |
0,971263 |
|
5,822222 |
2,198578 |
0,0363 |
0,013708 |
1,233679 |
0,476013 |
|
0,013708 |
0,986292 |
|
6,822222 |
2,576196 |
0,0147 |
0,005551 |
0,499589 |
|
|
0,005551 |
0,994449 |
15,086 |
|
|
|
|
Кр.согл. |
13,33343 |
|
|
|
|
Число степеней свободы в данном случае равно
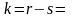14-9=5
Задаем уровень значимости q1=0,1 (при уровне надежности Р=0,9). По табл. Приложения 3 находим граничные значения отклонений
;
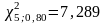Ответ:
Условие 7,289<13,33<15,086 выполнено, следовательно, распределение можно считать нормальным.
Задача 2.
Проведено 16 измерений шага зуба (хi , мм) зубчатого барабана. Полученные значения приведены в таблице 1.12. Проверить нормальность распределения данной погрешности.
Таблица 1.12
Результаты измерений шага зуба
4,72 |
4,71 |
4,73 |
4,74 |
4,70 |
4,72 |
4,74 |
4,73 |
4,70 |
4,74 |
4,71 |
4,69 |
4,72 |
4,70 |
4,71 |
4,72 |
Решение:
1. Находим среднее арифметическое
значение
,
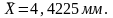2. Находим для всех 16 значений.
3. рассчитывают . В данном случае эта сумма равна 1,755 мм.
4. Находим
. В
данном случае
.
5. Статистика будет равна
.
6. Задаем уровень значимости . Для нахождения граничных значений статистик используем Приложение 4.
Первый критерий не выполняется
7. Проверяем второй критерий.
Задаем уровень значимости второго критерия q2=0,02.
Используя Приложение 6, находим , тогда
По Приложению 5 находим , учитывая, что .
Далее рассчитываем произведение
Просматриваем величины разностей и убеждаемся, что все значения больше.