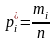Задача 4.1. Проверка гипотезы о нормальности закона распределения вероятности появления результатов измерений и их погрешностей при большом число результатов
Теоретическая часть.
Вид закона распределения вероятности может быть определен графически и аналитически. Аналитически вид распределения определяется при сравнении параметров данного (эмпирического) и теоретического распределений.
При проверке гипотезы о нормальности распределения проверяют равенство среднего арифметического и дисперсии эмпирического распределения математическому ожиданию и дисперсии нормального распределения.
Мера расхождения по Пирсону обозначается
(критерий согласия)
, (1.11)
где
,
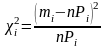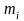- частоты, равные числу результатов в
каждом интервале, меньших или равных
его правой или больших левой границы;
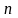- общее число результатов;
- теоретическая вероятность;
- ширина интервала;
- плотности в серединах интервалов;
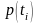- плотности нормированного распределения,
определяются по табл. Приложения 2 по
;
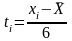- нормированное отклонение от среднего
арифметического;
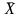- среднее арифметическое;
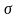- среднеквадратическое отклонение;
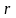- число интервалов.
Для каждого интервала вычисляют величины
,
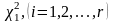суммируют, находят меру расхождения
.
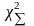Если в интервал входят 5 и меньше
значений, этот интервал объединяют с
соседним.
Определяют число степеней свободы
,
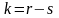где - число разрядов гистограммы;
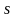- число независимых связей, к ним
относятся: равенство среднего
арифметического эмпирического и
теоретического распределений; равенство
математических ожиданий; равенство
суммы частностей единице.
Задают уровень значимости
, где 
- принятая доверительная вероятность
(надежность).
По табл. Приложения 3 находят значения
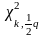и
.
Если
≤
≤
,
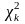то распределение считается нормальным.
Пример 4.1. Проверить нормальность распределения 100 результатов измерений среднего диаметра резьбового калибра. Результаты измерений приведены в таблице 1.8.
Таблица 1.8
Результаты измерений среднего диаметра резьбового калибра
Номер интервала |
хi min , мм |
хi max , мм |
Частоты mi |
Частости
|
1 |
8,911 |
8,913 |
1 |
0,01 |
2 |
8,913 |
8,915 |
5 |
0,05 |
3 |
8,915 |
8,917 |
14 |
0,14 |
4 |
8,917 |
8,919 |
27 |
0,27 |
5 |
8,919 |
8,921 |
24 |
0,24 |
6 |
8,921 |
8,923 |
18 |
0,18 |
7 |
8,923 |
8,925 |
9 |
0,09 |
r=8 |
8,925 |
8,927 |
2 |
0,02 |
Решение:
Диапазон значений составляет от 8,911 до
8,927 мм. Этот диапазон разбит на 8 интервалов
шириной 0,002 мм. В каждом интервале
рассчитывают частости
. Рассчитывают среднее арифметическое
значение (1.1)
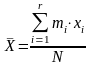
Вычисляют среднеквадратическое значение
(1.3)
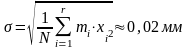
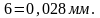
Далее для расчета критериев согласия по интервалам и суммарного критерия согласия составляют и заполняют табл. 1.9.
Число степеней свободы в данном случае равно
,
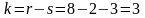так как два интервала были объединены, а число независимых связей s=3.
Задаем уровень значимости q1=0,1 (при уровне надежности Р=0,9). По табл. Приложения 3 находим граничные значения отклонений
;
.
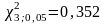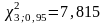Условие 0,352<1,125<7,815 выполнено, следовательно, распределение можно считать нормальным.
Таблица 1.9
Результаты расчетов
Номер интервала, i |
Середина интервала, хi , мм |
Частота, mi |
xi-X , мм
|
Нормированное отклонение t = (xi-X) / 6 |
Плотность нормированного распределения p(ti) Приложение.2 |
Плотность в середине интервала p(xi)=p(ti) / 6 |
Теоретическая вероятность nPi= ∆ xi p(xi)n |
Отклонение χi 2 |
1 |
8,912 |
1 |
-0,00736 |
-2,53 |
0,0163 |
5,8 |
1,16 |
0,018 |
2 |
8,914 |
5 |
-0,00536 |
-1,92 |
0,0632 |
22,6 |
4,52 |
|
3 |
8,916 |
14 |
-0,00336 |
-1,20 |
0,1942 |
69,5 |
13,9 |
0,007 |
4 |
8,918 |
27 |
-0,00136 |
-0,49 |
0,3546 |
126,7 |
25,34 |
0,109 |
5 |
8,920 |
24 |
+0,00064 |
+0,23 |
0,3885 |
138,8 |
27,76 |
0,509 |
6 |
8,922 |
18 |
+0,00264 |
+0,94 |
0,2558 |
91,3 |
18,26 |
0,004 |
7 |
8,924 |
9 |
+0,00464 |
+1,66 |
0,1006 |
36,0 |
7,2 |
0,4850 |
8 |
8,926 |
2 |
+0,00664 |
+2,37 |
0,0241 |
8,6 |
1,72 |