- •Министерство сельского хозяйства
- •Факультет инженерный
- •Аннотация
- •Содержание
- •Введение
- •1 Расчет параметров посадки с зазором
- •1.1 Основные теоретические сведения
- •1 Рассчитать параметры посадок гладких цилиндрических соединений: верхнее и нижнее отклонения вала и отверстия, предельные размеры и допуски деталей, характеристики посадки
- •2 Расчет параметров переходной посадки
- •2.1 Основные теоретические сведения
- •3 Выбор и расчет посадки с натягом
- •3. Рассчитать и выбрать посадку с натягом, определить ее параметры
- •4 Выбор и расчет параметров подшипника качения
- •4 Рассчитать и выбрать посадки для подшипника качения № _216____
- •5 Выбор и расчет посадок шпоночного соединения
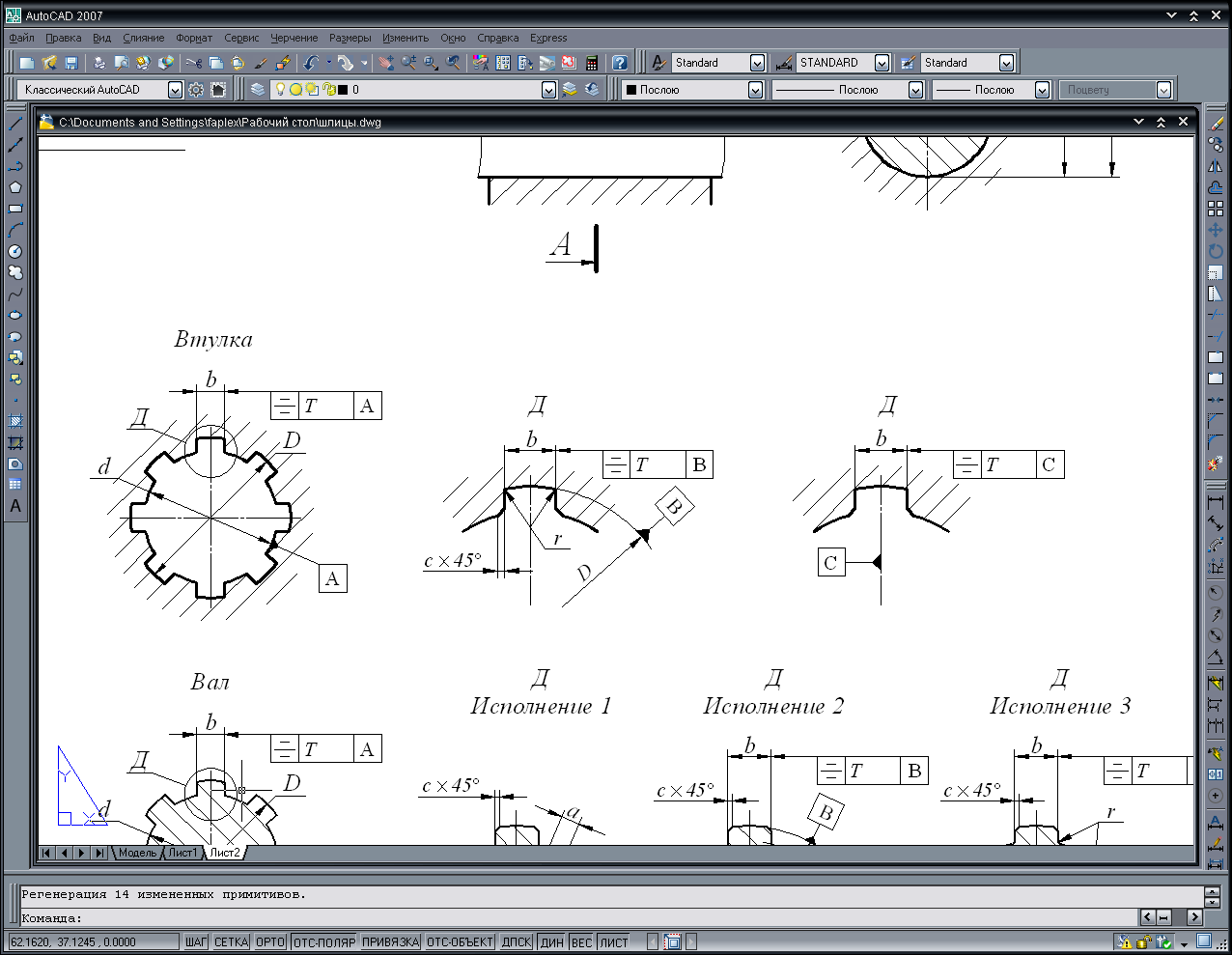
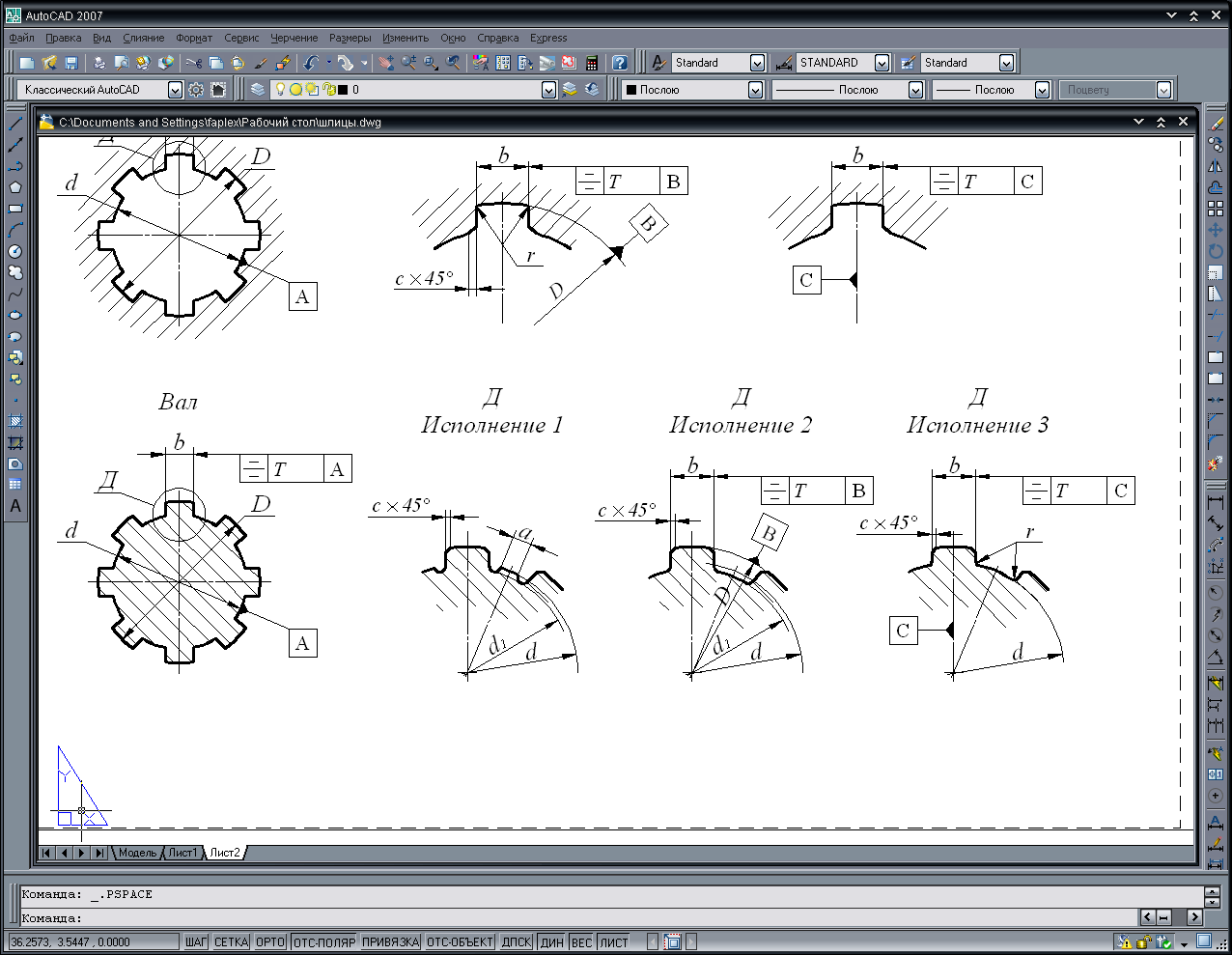
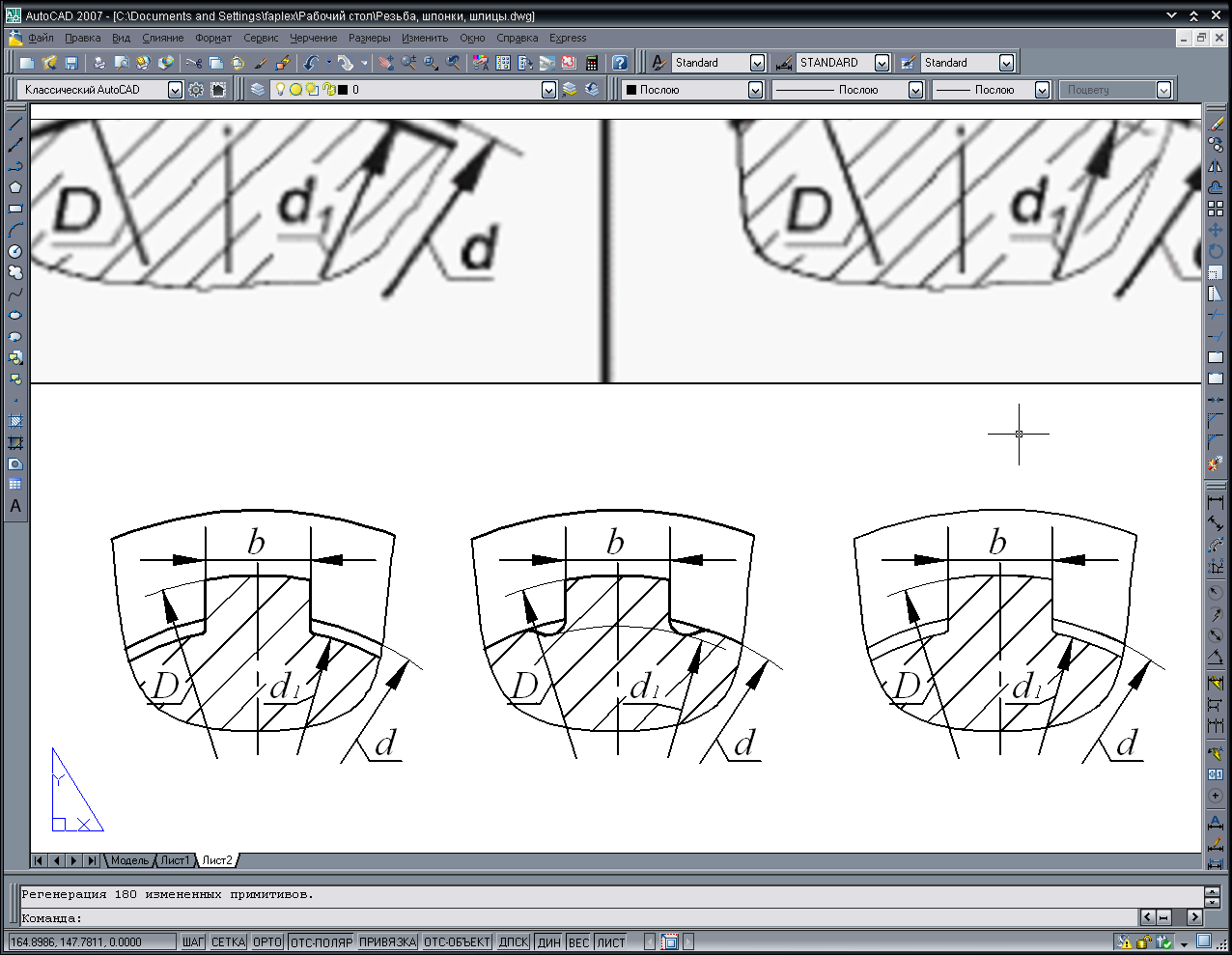
- •6 Выбор и расчет посадок шлицевого соединения
- •6 Выбрать посадки шлицевого соединения и рассчитать их параметры
- •7 Расчет метрологической оценки результата косвенного измерения
- •Литература
7 Расчет метрологической оценки результата косвенного измерения
Основные теоретические сведения
Целью любых измерений является получение результата измерения, то есть значения физической величины, найденного путем ее измерения. Однако на практике не удается получить значение физической величины, которое бы идеальным образом отражало ее истинное значение. В связи с этим возникает проблема определения того ,насколько результат измерения отклоняется от истинного значения измеряемой величины, то есть проблема определения погрешности измерения. На важность задачи метрологической оценки результатов измерений указывает тот факт, что этот вопрос выделен в специальный раздел метрологии.
При этом определяются следующие погрешности:
Средняя арифметическая погрешность единичного измерения в ряду измерений – определяется как среднее арифметическое значение из абсолютных значений i-ых погрешностей, присущих ряду измерений.
Средняя квадратическая погрешность единичного измерения в ряду из n измерений – это обобщенная характеристика рассеяния результатов, полученных в ряду независимых измерений одной и той же величины, вследствие влияния случайных погрешностей.
Погрешность определения средней квадратической погрешности – оценивается на практике при ограниченном числе измерений.
Средняя квадратическая погрешность результата измерения.
Средняя квадратическая погрешность результата косвенных измерений – величина, являющаяся функцией нескольких переменных.
Доверительный интервал погрешности результата измерений – это интервал, в который попадает измеряемая величина Х с заданной вероятностью Р.
 Исходные
данные для расчета
Исходные
данные для расчета
I U R |
||||||||||
№ |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
U, В |
381 |
382 |
385 |
- |
389 |
390 |
395 |
397 |
399 |
- |
R, Ом |
116 |
117 |
118 |
120 |
121 |
130 |
130,5 |
131 |
134 |
- |
Расчет метрологической оценки результата косвенного измерения
Выполнение метрологической оценки результата косвенного измерения действительной постоянной прибора измеряющего электрический ток:

где U – напряжение;
R – сопротивление.
Определяем среднюю арифметическую погрешность единичного измерения в каждом ряду измерений:
для U:
-
среднее арифметическое из n
значений
величины
 :
:
 (7.1)
(7.1)
 (В)
(В)
- средняя арифметическая погрешность единичного измерения в ряду
измерений – rU:
 (7.2)
(7.2)
 (В)
(В)
 Аналогично
определяем для
R:
Аналогично
определяем для
R:
 (Ом)
(Ом)
 (Ом)
(Ом)
Определяем среднюю квадратическую погрешность единичного измерения в ряду измерений:
для U:
 (7.3)
(7.3)
 (В)
(В)
Аналогично определяем для R:
 (
Ом)
(
Ом)
Выполняем проверку соотношения между r и S в каждом ряду:
 (7.4)
(7.4)
для U:

для R:

Вывод: так как n = 9 < 18, то и выполнение этих условий приблизительно.
Определяем погрешность определения средней квадратической погрешности:
для U:
 (7.5)
(7.5)
 (В)
(В)
для R:
 (Ом)
(Ом)
 Следовательно,
значение
Следовательно,
значение
 лежит в диапазоне от 32,84 (43,78-10,94=32,84) до
54,72 (43,78+10,94=54,72) и можно записать:
лежит в диапазоне от 32,84 (43,78-10,94=32,84) до
54,72 (43,78+10,94=54,72) и можно записать:
 В (находим среднее и округляем до целого).
В (находим среднее и округляем до целого).
Аналогично
 лежит в диапазоне от 5,33 до 8,87 и можно
записать
лежит в диапазоне от 5,33 до 8,87 и можно
записать
 Ом.
Ом.
Записываем окончательные результаты рядов измерений.
для
U:

для
R:
 .
.
Определяем среднюю квадратическкую погрешность результата измерения:
для U:
 В
В
для R:
 Ом
Ом
Определяем среднюю квадратическкую погрешность результата косвенного измерения I:
Так как , то I=f(U,R). Тогда:
 (7.6)
(7.6)
Находим производные:


Находим квадраты производных:


 Тогда
Тогда (А)
(А)
Вычисляем границы доверительного интервала погрешности результата измерения:
 ,
где tS
=2,31
так
как n
=9, P
=0,95
,
где tS
=2,31
так
как n
=9, P
=0,95
 .
.
Тогда, согласно правилу записи результатов измерения:
 ,
,
где
 (А).
(А).
 (А)
при Р
=0,95, n
=9.
(А)
при Р
=0,95, n
=9.
И доверительный интервал результата измерения с вероятностью 0,95 будет равен (2,5; 3,08).
Таблица 1 – Параметры шлицевых соединений с прямобочным профилем зубьев
|
||||||
z d D b, мм (z – число зубьев) |
d1, мм |
a, мм |
с, мм |
r, мм, не более |
||
не менее |
||||||
Легкая серия |
||||||
6 23 26 6 |
22,1 |
3,54 |
0,3 |
0,2 |
||
6 26 30 6 |
24,6 |
3,85 |
0,3 |
0,2 |
||
6 28 32 7 |
26,7 |
4,03 |
0,3 |
0,2 |
||
Таблица 2 –посадки шлицевых соединений с прямобочным профилем зуба
Чертеж сопряжения |
|
|
|
||||||
Центрирующий элемент |
Центрирование по D |
Центрирование по d |
Центрирование по b |
||||||
Посадки |
По d |
По D |
По b |
По d |
По D |
По b |
По d |
По D |
По b |
Подвижное соединение |
- |
|
|
|
|
|
- |
|
|
Примечания. 1. Посадки, заключенные в рамку, являются предпочтительными. |
|||||||||

Заключение
В ходе выполнения данной курсовой работы, была проанализирована справочная, нормативно-техническая документация, определяющая порядок и устанавливающая требования к нормированию показателей качества деталей машин, как основы качественной работы всего механизма в целом.
Были рассчитаны параметры посадок с зазором и переходной, выбрана и рассчитана посадка с натягом, выполнен выбор и расчет посадок колец подшипников качения, шпоночного, шлицевого, и метрологической оценки результата косвенного измерения.