Результаты измерений параллельного соединения

¦, Гц	Uсети, В	С, мкФ	I, А	IK, А	IC, А

4.3.3. По данным таблицы 6.2 постройте резонансную кривую I = F(C).

4.4. Сделайте выводы по работе.

Контрольные вопросы.

1. Как определить полное сопротивление реальной катушки?

2. Как определить ток в цепи реальной катушки?

3. Как выглядит векторная диаграмма для цепи реальной катушки?

4. Как определить угол сдвига между напряжением и током в цепи реальной катушки?

5. При каком соединении реальной катушки и конденсатора в цепи может возникнуть резонанс напряжений, а при каком резонанс токов?

6. В чем заключается явление резонанса (напряжения, тока)?

7. Какую мощность потребляет от источника переменного тока цепь реальной катушки и конденсатора при возникновении в ней резонанса напряжений?

8. Чему равен угол сдвига между напряжением и током в цепи при резонансе (напряжения, тока)?

9. Какие мощности потребляет от источника цепь реальной катушки и конденсатора при возникновении в ней резонанса токов?

Лабораторная работа 4. Цепи трехфазного переменного тока.

Ц е л ь р а б о т ы: изучить особенности соединения источников и приемников трехфазного переменного тока звездой и треугольником; на основе экспериментов уяснить возможность работы потребителей при симметричной и несимметричной нагрузках и в аварийных режимах.

1. Задание к самостоятельной работе.

1. Изучите принцип получения трехфазного переменного тока, особенности соединения фаз генератора и потребителей звездой и треугольником /1, с.56-144/, /2, с.107-114/, /3, с.104-114/, /6, с.52-58/.

2. Запишите: правила соединения звездой и треугольником, соотношения линейных и фазных напряжений и токов.

3. Изучите методику построения векторных диаграмм напряжений и токов при симметричной и несимметричной нагрузках и в аварийных режимах /1, с.144-148/, /2, с.114-122/, /3, с.116-118/.

4. Ответьте на контрольные вопросы:

2. Общие сведения.

1. Основные определения и термины в цепях трехфазного тока.

Прежде чем приступить к экспериментальному исследованию, необходимо понять принцип получения трехфазного тока, особенности его передачи и правила подключения потребителей. Обратите внимание на терминологию.

Трехфазной системой называется цепь переменного тока, в которой действуют три синусоидальные ЭДС одинаковой частоты, взаимно смещенные по фазе на 120^о, или 1/3 периода (рис.7.1). Мгновенные значения ЭДС обозначены е_А , е_В , е_С; амплитудные значения Е_МА, Е_МВ, Е_МС

Рис.7.1. Волновая диаграмма трехфазной цепи.

Трехфазная цепь состоит из генератора трехфазного переменного тока, приемников (потребителей электрической энергии) и соединительных проводов. Каждую из однофазных цепей, образующих трехфазную систему, называют фазой. В практике широко применяется соединение фаз по схемам звезда и треугольник.

Звездой называется такой вид соединения, при котором концы фаз генератора или приемников соединены в одну точку, называемую нейтральной или нулевой точкой (рис.7.2).

Провода Аа, Вв, Сс, отходящие от начала фаз генератора, называются линейными.

Провод Nn, соединяющий нейтральные точки генератора и приемников, называется нейтральным, а сеть - четырехпроводной.

Обрыв нулевого провода может привести к нарушению работы потребителей, поэтому в него нельзя ставить ни выключатели, ни предохранители.

В сетях с напряжением до 1000В нейтральный провод сети соединяется с землей (заземляется). В этом случае к нему присоединяют металлические части электроустановок, нормально не находящиеся под напряжением (например, корпуса электродвигателей, трансформаторов и т.д.) для обеспечения безопасности людей и животных при авариях - пробое изоляции и попадании напряжения на корпуса этих электроустановок.

Рис.7.2. Схема соединения потребителей звездой.

Треугольник получают, соединяя конец 1-й фазы Х с началом 2-й фазы В, конец второй фазы Y с началом 3-й фазы С и конец третьей фазы Z с началом 1-й фазы А (рис.7.3).

Точки соединения начала и конца фаз генератора служат для отвода трехфазного тока. Отходящие от них провода называются линейными, а сеть - трехпроводной.

Z_а, Z_в, Z_с (рис.5.2), Z_ав, Z_вс, Z_са (рис.7.3) - сопротивления фаз приемников. Если сопротивления фаз одинаковы по величине и характеру (активные, индуктивные, емкостные), нагрузка называется симметричной. Если эти условия не выполняются, нагрузка называется несимметричной.

Напряжение, измеренное между началом и концом фазы генератора или приемника или между линейным и нейтральным проводом, называется фазным. Фазные напряжения обозначаются U_а, U_в, U_с или в общем случае U_Ф.

Напряжения между началами фаз или между линейными проводами сети называются линейными. Они обозначаются U_АВ, U_ВС, U_СА или в общем случае U_Л.

Рис. 7.3. Схема соединения потребителей треугольником.

Из рисунков 7.2 и 7.3 видно, что при соединении треугольником линейные напряжения равны фазным: U_Л = U_Ф. А при соединении звездой: U_Л= Ö3U_Ф (рис.7.2, 7.5.б).

Потребители трехфазного тока включаются в сеть звездой или треугольником. Схема включения выбирается в зависимости от величины напряжения, на которое рассчитана каждая фаза потребителя. Так, в сеть 380/220В потребители, рассчитанные на напряжение 220В должны включаться звездой. Если же они рассчитаны на 380В, то включаются треугольником (рис.7.4).

Рис.7.4. Схемы включения трехфазных потребителей:

а) звездой; б) треугольником

В замкнутых электрических цепях трехфазной системы протекают токи. В фазах генератора и приемников они называются фазными и обозначаются I_Ф (токи I_а, I_в, I_с на рисунке 7.2 и токи I_ва, I_вс, I_са на рисунке 7.3). В линейных проводах сети токи называются линейными и обозначаются I_Л (токи I_А, I_В, I_С). Ток в нейтральном проводе обозначается I_N. Из схем (рис.7.2 и 7.3) и векторных диаграмм (рис.7.6 и 7.11.а) видно, что при соединении звездой линейные токи равны фазным I_Л = I_Ф, а при соединении треугольником симметричной нагрузки линейный ток в Ö3 раз больше фазного I_Л = Ö3 I_Ф.

2. Методика построения векторных диаграмм.

Для анализа работы трехфазной цепи строятся векторные диаграммы токов и напряжений. За условные положительные направления векторов фазных напряжений и токов принято направление от начала к концу фазы (рис.7.2 и 7.3), а линейных напряжений - от начала одной фазы к началу другой (рис.7.2).

2.2.1. Соединение звездой.

Рассмотрим построение векторной диаграммы на примере трехфазной цепи с нейтральным проводом. Векторная диаграмма напряжений строиться следующим образом: из точки n (рис.7.5.а) откладываем три одинаковых вектора фазных напряжений, сдвинутых относительно друг друга на 120^о. Векторы линейных напряжений строим исходя из второго закона Кирхгофа: . Так, для построения вектора необходимо из конца вектора (рис.7.5.а) отложить вектор - , равный , но противоположный ему по направлению, и соединить начало вектора с концом вектора - . То же самое получим, если соединим начала векторов и (на рис.7.5.а вектор ^/₌ показан штриховой линией). По этому принципу построена векторная диаграмма на рис.7.5.б. Пользуясь ей, легко определить величину линейного напряжения при схеме звезда: U_л=Ö3U_ф.

Если фазное напряжение генератора 220В, то линейное напряжение составит U_л = Ö3 ×220 = 1,73 ×220 = 380В. Напряжение трехфазной четырехпроводной сети записывают так: 380/220В. Каждая фаза приемников, включенных в такую сеть звездой, будет находиться под напряжением 220В и должна быть на него рассчитана (рис.7.2).

Рис.7.5. Векторная диаграмма напряжений трехфазной цепи с нейтральным проводом.

2.2.1.1. Анализ работы трехфазной цепи с нейтральным проводом при различных режимах нагрузки.

Приемники, включенные в трехфазную сеть, могут быть симметричными и несимметричными. Условие симметрии приемников - равенство сопротивлений всех фаз (Z_а=Z_в=Z_с=Z_ф) и равенство углов сдвига между токами и напряжениями в фазах при одинаковом характере нагрузки: активном, индуктивном или емкостном (j_а=j_в=j_с=j). При активной нагрузке фазный ток совпадает по фазе со своим напряжением (j=0), при индуктивной нагрузке - отстает, а при емкостной - опережает напряжение по фазе на j=90^о.

В случае симметричной нагрузки токи во всех фазах будут одинаковы и будут сдвинуты относительно друг друга на углы 120^о.

I_а = I_в = I_с = I_ф = U_ф/ Z_ф.

Ток в нейтральном проводе в соответствии с рис.7.2 равен:

Построим векторную диаграмму токов при симметричной нагрузке и произведем сложение векторов фазных токов (рис.7.6).

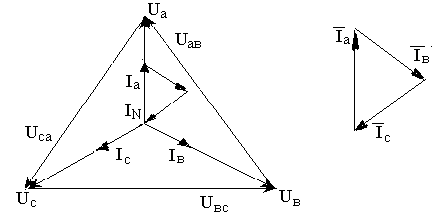
Рис.7.6. Векторная диаграмма токов при симметричной нагрузке.

Следовательно, при симметричной нагрузке ток в нейтральном проводе отсутствует и приемники могут нормально работать без него (рис.7.8). Все фазы приемников будут находиться под одинаковыми напряжениями U_Ф=U_Л/Ö3.

Если нагрузка несимметричная (не равны сопротивления фаз Z_Ф или углы сдвига j), в нейтральном проводе сети появится ток (рис.7.7) в соответствии с уравнением

Рис.7.7. Векторная диаграмма токов при несимметричной нагрузке фаз (при наличии нейтрального провода).

2.2.1.2. Анализ работы трехфазной цепи без нейтрального провода при несимметричной нагрузке.

При обрыве или отключении нейтрального провода (рис.7.8) в сети сохраняются три одинаковых по величине линейных напряжения, сдвинутых относительно друг друга на 120^о (векторы U_ав, U_вс, U_са на рис.7.5.б).

Рис.7.8. Схема соединения приемников звездой без нейтрального провода.

Сделаем нагрузку несимметричной, для чего будем изменять величину сопротивления фазы Z_а. С уменьшением Z_а ток в ней возрастет, а напряжение U_а уменьшится. На двух других фазах напряжение увеличится, и потребители этих фаз могут выйти из строя (рис.7.9.а). Нейтральная точка сместится из центра диаграммы по направлению к точке «а» и займет положение «n». Между нейтральным проводом сети N и нейтралью приемников появится напряжение U_N. Очевидно, что при Z_а=0, что соответствует короткому замыканию фазы, напряжение U_а=0. Построив для этого случая векторную диаграмму, убедитесь, что напряжения U_в и U_c станут равны линейным.

Рис.7.9. Векторная диаграмма напряжений и токов при активно-индуктивной нагрузке без нейтрального провода: а) режим короткого замыкания; б) обрыв линейного (фазного) провода

С увеличением Z_а величина тока в ней уменьшится, а напряжение будет расти. Потребители этой фазы выйдут из строя. На двух других фазах напряжения будут снижаться (рис.7.9.б).

При Z_а=¥, что соответствует обрыву внутри фазы или обрыву линейного провода Аа, напряжение U_а достигнет максимального значения U_а = U_л cos30^о. Напряжения на других фазах будут равны U_в = U_с = U_л/2.

Установим различные сопротивления фаз, например, Z_а > Z_в > Z_с. Напряжения на фазах распределятся пропорционально их сопротивлениям: U_а>U_в >U_с (рис.7.10.а).

При несимметричной нагрузке без нейтрального провода сумма фазных токов в точке n, согласно первому закону Кирхгофа, должна равняться нулю. Векторы токов на векторной диаграмме нужно строить с учетом направления соответствующих векторов фазных напряжений. Например, векторной диаграмме напряжений (рис.7.10.а) при включении активной нагрузки будет соответствовать векторная диаграмма токов (рис.7.10.б), где каждый вектор тока отложен параллельно вектору своего фазного напряжения. Складывая векторы, получим, что их сумма равна нулю.

Рис. 7.10. Векторные диаграммы напряжений (а) и токов (б) при несимметричной активной нагрузке без нейтрального провода.

Таким образом, изменение сопротивления хотя бы одной из фаз приемника вызывает при обрыве нейтрального провода перераспределение фазных напряжений и нарушает нормальную работу потребителей. На фазах с меньшей нагрузкой (т.е. большим сопротивлением) напряжение повышается, и потребители выходят из строя, фазы с большей нагрузкой (меньшим сопротивлением) не развивают свою паспортную мощность. Поэтому соединение звездой без нейтрального провода при несимметричной нагрузке не применяется.

В случае несимметричной нагрузки нейтральный провод сети выравнивает напряжение на фазах приемника и обеспечивает их нормальную работу.

2.2.2. Соединение треугольником.

Линейные напряжения сети изображаются тремя одинаковыми векторами U_АВ, U_ВС, U_СА, сдвинутыми относительно друг друга на 120^о (рис.7.11).

Векторы фазных токов откладываются от начала соответствующих напряжений в зависимости от характера нагрузки: при активной нагрузке токи совпадают по фазе с напряжениями, при индуктивной - отстают, при емкостной - опережают напряжения. Векторные диаграммы на рис.7.11 построены для активной симметричной (а) и несимметричной (б) нагрузок.

Векторы линейных токов строят, используя векторные уравнения для узловых точек на основании 1-го закона Кирхгофа:

(·) А

(·) В

(·) С

Для построения вектора линейного тока необходимо из конца вектора отложить вектор , изменив его направление на 180⁰. Замыкающий вектор равен . Аналогично строим векторы и .

Рис.7.11. Векторные диаграммы при соединении приемников треугольником: а) симметричная нагрузка; б) несимметричная нагрузка (Z_ав>Z_вс>Z_са).

Из треугольника DON (рис.7.11.а) находим, что I_а= Ö3I_ав. Таким образом, при соединении треугольником симметричной нагрузки линейный ток в Ö3 раз больше фазного: I_Л = Ö3 I_Ф.

При несимметричной нагрузке (рис.7.11.б) векторы напряжений не изменяются, а меняются в соответствии с законом Ома величина фазных токов I_Ф = I_Л/Z_Ф и направление их векторов. Соответственно изменяются величины и направления векторов линейных токов.

2.2.2.1. Анализ работы потребителей, соединенных треугольником в аварийных режимах.

2.2.2.1.1. Обрыв в одной из фаз приемника. Сопротивление этой фазы равно бесконечности, ток I_Ф= 0 (рис.7.12.а).

Из векторной диаграммы (рис.7.12.б) видим, что линейный ток I_С остается неизменным, а линейные токи I_А и I_В стали равными соответствующим фазным токам: I_А= I_са, I_В = I_вс. Напряжения на исправных фазах не изменились, величина токов осталась прежней, т.е. нормальная работа этих фаз потребителя не нарушилась.

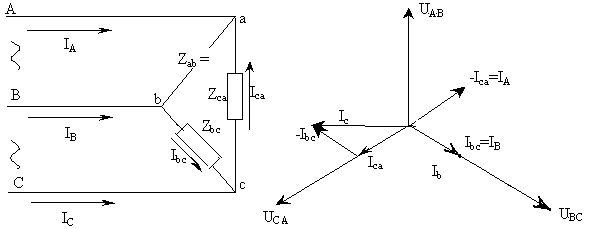
Рис.7.12. Схема (а) и векторная диаграмма (б) при обрыве одной из фаз приемника, соединенного треугольником.

2.2.2.1.2. Обрыв линейного провода сети (провод Вв на рис.7.13.а) превращает трехфазную цепь в однофазную. Приемники фаз Z_ав и Z_вс оказываются соединенными последовательно, и по закону Ома ток в них снизится в два раза (при Z_ав=Z_вс). Ток I_са не изменится. Векторная диаграмма для этого случая показана на рис.7.13.б.

а) б)

Рис.7.13. Схема (а) и векторная диаграмма (б) при обрыве линейного провода сети (соединение треугольником).

В данном случае только потребители фазы Z_са будут работать нормально, так как напряжение на них не изменилось. Потребители фаз Z_ав и Z_са находятся под пониженным в два раза напряжением.