Свойства средней арифметической:

1. 

2. 

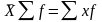
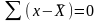
3. Если каждую варианту разделить или умножить на какое-либо число, то средняя арифметическая уменьшится или увеличится во столько же раз.

4. Если каждую варианту уменьшить или увеличить, то средняя арифметическая уменьшится или увеличится на это же число.

5. Если все частоты разделить или умножить на какое-то число, то средняя арифметическая от этого не изменится.

26. Расчет средней по результатам группировки.(интеренет)

 Данные для расчета и анализа средних величин могут быть представлены в сгруппированном виде, когда для каждого значения усредняемого признака         Х сообщается частота его повторения. В этих случаях средняя величина рассчитывается по обычным формулам средних взвешенных (арифметических либо гармонических). Если в сгруппированных данных указывается не конкретное значение признака         Х по каждой группе, а лишь интервал его изменения, то в этом случае необходимо получить среднее значение признака по каждой группе. А далее используются обычные формулы средних взвешенных. Если же средние значения признака в группах определить по имеющимся сведениям нельзя, то их заменяют условно значениями центра интервалов. В результате получают ряд распределения, аналогичный дискретному, где в качестве значений дискретного признака будут выступать центры интервалов аi,а в качестве весов признака Fi        - количество элементов ряда для интервала i.        Таким образом, расчет средней арифметической делают по формуле        Показательсебестоимостиявляется вторичным признаком, так как он задан на единицу первичного признака (объем продукции, выраженный абсолютной величиной) и может быть представлен как отношение двух первичных признаков, а именнозатрат на производствоиобъём продукции:        С = ЗП / ОП, где С — себестоимость, ЗП — затраты на производство, ОП —.объем продукции.        Следовательно, для расчета средней себестоимости по каждому предприятию следует вычислить среднюю взвешенную. Нужно выбрать: арифметическую или гармоническую?        Выбор вида средней усредняемого признака выполняется по следующим правилам.        1. Если в условии задачи даны численные значения числителя и знаменателя логической формулы показателя, средняя величина вычисляется непосредственно по этой формуле.        2. Если имеется ряд данных по двум взаимосвязанным показателям, для одного из которых нужно вычислить среднюю величину, и при этом известны численные значения знаменателяеёлогической формулы, а значения числителя не известны, но могут быть найдены как произведения этих показателей, то средняя должная вычисляться по формулесредней арифметической взвешенной.        3. Если известны численные значения числителя логической формулы, а значения знаменателя не известны, но могут быть найдены как частное от деления одного показателя на другой, то средняя вычисляется по формулесредней гармонической.        Среднюю гармоническую применяют для расчетов тогда, когда в качестве весов используются не единицы совокупности — носители признака, а произведения этих единиц на значения признака (т. е. m = X*f). К средней гармонической простой следует прибегать в случаях определения, например, средних затрат труда, времени, материалов на единицу продукции, на одну деталь по двум (трем, четырем и т. д.) предприятиям, рабочим, занятым изготовлением одного итого же вида продукции, одной и той же детали, изделия.        Общее требование к формуле расчета среднего значения состоит в том, чтобы все этапы расчета имели реальное содержательное значение. Полученное среднее значение должно заменить индивидуальные значения признака у каждого объекта без нарушения связи индивидуальных и сводных показателей. Иначе говоря, средняя величина должна исчисляться так, чтобы при замене каждого индивидуального значения усредняемого показателя его средней величиной оставался без изменения некоторый итоговый сводный показатель, связанный с усредняемым. Этот итоговый показатель является определяющим в том смысле, что его связь с индивидуальным значением признака определяет способ расчета средней величины.  

27. Структурные средние, их использование в статистике.

Наиболее распространенными среди структурных средних являются мода и медиана.

Мода – величина признака, которая наиболее часто встречается в данной совокупности.

Если признак, по которому определяется модальное значение, представлен интервалом, то конкретное значение моды определим по формуле Орджетцкого.

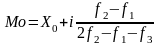, где:

X₀ - нижняя граница модального интервала;

i - шаг интервала;

f₁ - частота предмодального интервала;

f₂ - частота модального интервала;

f₃ - частота послемодального интервала.

Мода дает возможность определить преобладающий исследуемый уровень в данный момент.

Если в распределении 2 варианты имеют общую частоту, то такое распределение мультимодальное. Мультимодальное распределение характерно для неоднородной совокупности.

Если интервальный ряд представлен неравными интервалами, то применяется плотность распределения – рассчитывается как частное отделение частоты на величину принятого интервала.

Медиана – признак, характеризующий варианту, стоящую в середине ранжированного вариационного ряда. Положение медианты определяется ей номером. Номер медианы определяется следующим образом:

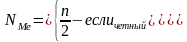
В дискретном ряду, медиана определяется по накопленным частотам.

В интервальных вариационных рядах сначала по накопленным частотам определяется интервал, в котором она находится, а затем по форму Орджетцкого определяется конкретное значение медианы.

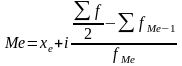, где:

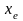- нижняя граница медианного интервала;

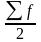- номер медианы;

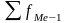-накопленная частота предмедианного интервала;

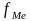- частота медианного интервала.

Медиана обладает следующим свойством: сумма отклонения каждого члена ряда от медианы является наименьшей величиной. Благодаря этому свойству, медиану используют при оптимизации каких-либо процессов.

Наряду с медианой для характеристики структуры используются квартири и децири. Квартири делят ряд по сумме накопленных частот на 4 равные части, а децири на 10 равных частей.

Медиана может быть использована вместо средней величины, если имеет место рассеивание совокупности по краям вариационного ряда.

28. Взаимосвязь абсолютных и относительных величин, их комплексное использование.

29. Виды относительных величин, взаимосвязь.

 Абсолютной величиной называется показатель, выражающий размеры социально-экономического явления.

       Относительной величиной в статистике называется показатель, выражающий количественное соотношение между явлениями. Он получается в результате деления одной абсолютной величины на другую абсолютную величину. Величина с которой мы производим сравнения называетсяоснованием или базой сравнения.

       Абсолютные величины - всегда величины именованные.

       Относительные величины выражаются в коэффициентах, процентах, промили и т.д.

       Относительная величина показывает, во сколько раз, или на сколько процентов сравниваемая величина больше или меньше базы сравнения.

       В статистике различают 8 видов относительных величин:

1. Относительная величина выполнения плана (ОВВП) показывает во сколько раз или на сколько процентов выполнено данное задание.

ОВВП= фактические данные отчетного периода

           плановые данные отчетного периода

2. Относительная величина планового задания (ОВПЗ) показывает во сколько раз или на сколько процентов плановое задание отчетного периода больше или меньше уровня базисного периода.

ОВПЗ= плановое число отчетного периода

           фактич. данные базисного периода

3. Относительная величина динамики (ОВД) показывает во сколько раз или на сколько процентов уровень отчетного периода больше или меньше уровня базисного периода.

ОВД= фактич. данные отчетного периода

         фактич. данные базисного периода

4. Относительная величина сравнения (ОВС) показывает во сколько раз или на сколько процентов явление на территории А больше или меньше явления на территории В.

ОВСр.= фактич. уровень явления на территории А за определенный период времени

           фактич. уровень того же явления за тот же период времени на территории В

5. Относительная величина интенсивности (ОВИ). Коэффициент рождаемости и т.д., число родившихся в определенной местности за определенный период времени.

ОВИ= фактич. уровень явления за опред. период времени

         размер среды в которой данное явление развивалось

6. Относительная величина координации (ОВК) рассчитывается только для сгруппированных данных и показывает отношение между частями совокупности.

ОВК= число единиц определенной группы

         число единиц группы, принятой за базу сравнения

7. Относительная величина структуры (ОВС).

ОВСт.= часть совокупности

         вся совокупность

8. Относительная величина уровня экономического развития (ОВУЭР)

ОВУЭР= годовой объем производства продукции

             среднегодовая численность населения

30. Показатели асимметрии и эксцесса, их назначение.(можешь почитать но надо что то другое искать,более краткое..)

Любое реальное распределение можно изобразить схематически в виде кривой, воспроизводящей основные особенности данного распределения. Под кривой распределения понимается графическое изображение в виде непрерывной линии изменения частот, функционально связанных с изменением вариант. 

Элементами распределения являются:

• варианта

• частота

В зависимости от вида кривых, изображающих распределение, выделяют несколько основных типов распределения:

• одновершинные

• многовершинные

К одновершинным относятся те, в которых один, обычно центральный вариант, имеет наибольшую частоту (плотность распределения). Частоты же остальных вариантов убывают по мере удаления от центрального. 

Если частоты убывают слева и справа от центрального значения одинаково, то такие распределения называются симметричными. 

Если частоты убывают слева и справа от центра распределения с разной скоростью, то такие распределения называют асимметричными. 

Многовершинные распределения – это распределения, в которых несколько центров, т. е. такие, у которых несколько максимумов  частот.

Для однородных совокупностей, как правило, характерны одновершинные распределения.

Многовершинность распределения свидетельствует о неоднородности изучаемого явления. В этом случае необходимо произвести перегруппировку данных с целью выделения более однородных групп.

Выяснение общего характера распределения предполагает, наряду с оценкой его однородности, вычисление показателей асимметрии и эксцесса.

Кривые распределения бывают:

1. симметричными

2. асимметричными.

В зависимости от того, какая ветвь кривой распределения вытянута, различают:

1. правостороннюю асимметрию

2. левостороннюю асимметрию.

Для характеристики степени асимметрии двух или нескольких рядов пользуются коэффициентом асимметрии.

Для одновершинных распределений:

  

Более точным является коэффициент асимметрии, рассчитанный как отношение центрального момента третьего порядка (μ³) к среднеквадратическому отклонению в 3-й степени (Ϭ³):

  

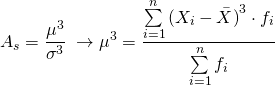
1. Для симметричного распределения: 

  

Соответственно, в симметричном распределении центральный момент 3-го порядка равен нулю (μ³=0), т. е. алгебраическая сумма отклонений отдельных значений признака (вариант), расположенных слева и справа от средней, равна нулю. График симметричного распределения симметричен относительно точки максимума.

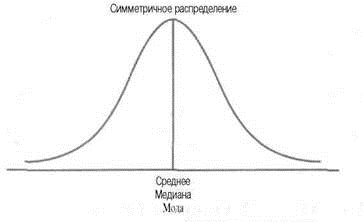
Для несимметричных распределений центральные моменты нечетного порядка отличны от нуля:

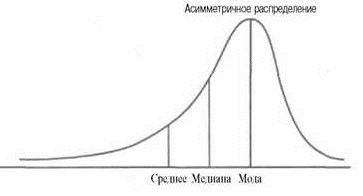
2. Асимметрия положительна (A_s>0), если длинная часть кривой распределения расположена справа от моды (М_о). В этом случае соотношение между средней, медианой и модой нарушено:

  

 3. Асимметрия отрицательна (A_s<0), если длинная часть кривой распределения расположена слева от моды (М_о).

  

 A_s< 0.25 – слабая асимметрия

A_s= 0.25-0.5 – умеренная асимметрия

A_s> 0.5 – крайне асимметричное распределение

Для оценки «крутизны» (островершинности) распределения пользуются характеристикой – эксцессом.

Коэффициент эксцесса:

  

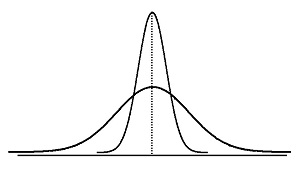
1. Для нормального распределения:

  

2. Выше нормального (островершинное распределение):

  

3. Ниже нормального (плосковершинное распределение):

  

Стр.138

31. Показатели вариации количественного признака, их роль.

32. Вариация признаков, способы ее изучения, критерии оценки.

33. Виды дисперсий. Правило сложения дисперсий.

Правило сложений дисперсий:

Для проведения факторного анализа возможно использование различных видов дисперсий:

1. Общая: 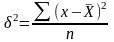- простая 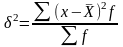- взвешенная Общая дисперсия улавливает влияние группы факторов:

   1. Положенного в основу группировки – систематический фактор;

   2. Случайной причины – оказывающей влияние на результат.

Таким образом, с помощью дисперсионного анализа можно выявить влияние систематического фактора и случайных величин на результат, а также оценить тесноту связи между фактором, положенным в основу группировки и результатом.

2. Межгрупповая дисперсия: выражает величину, обусловленную влиянием признака, положенного в основу группировки, выражает влияние систематического фактора.

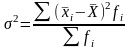, где: 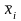- среднее значение факторного признака, положенного в основу группировки по отдельно взятой группе;

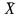- среднее значение факторного признака в целом по совокупности;

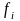-частота повторения в соответствующей группе.

3. Средняя внутригрупповая дисперсия – устанавливает влияние случайных величин.

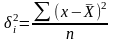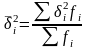- внутригрупповая дисперсия

- средняя внутригрупповая дисперсия