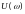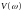- •Содержание:
- •II. Следящая система
- •III. Уравнения звеньев системы.
- •I. Исходные данные
- •II. Следящая система
- •2. Описание системы.
- •III. Уравнения звеньев системы и их передаточные функции. Составление структурной схемы системы.
- •V. Получение уравнения статики системы и его использование при расчете системы.
- •VI. Проверка системы на устойчивость. Критерий Вишнеградского.
- •VII. Определение параметров системы по наибольшей степени устойчивости.
- •Определение апериодической степени устойчивости:
- •2. Определение колебательной степени устойчивости:
- •3.Определение параметров линейной системы по наименьшей квадратичной интегральной оценке качества
- •VII. Исследование сау на устойчивость.
- •Проверка сау на устойчивость по методу Гурвица.
- •Проверка сау на устойчивость по методу Найквиста.
- •3. Проверка сау на устойчивость по методу Рауса.
- •4. Проверка сау на устойчивость по методу Михайлова.
- •VIII. Построение афх разомкнутой сау.
- •X. Построение лфчх разомкнутой системы.
- •XI.Построение лачх разомкнутой системы.
4. Проверка сау на устойчивость по методу Михайлова.
Критерий
устойчивости Михайлова является
наглядной графической интерпретацией,
т.е. характеристической
кривой
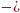 кривой Михайлова
. Суть в том,
что график начиная при
кривой Михайлова
. Суть в том,
что график начиная при
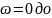 бесконечности
обходил последовательно в положительном
направлении (против часовой стрелки) n
квадрантов, где n-порядок
характеристического уравнения.
бесконечности
обходил последовательно в положительном
направлении (против часовой стрелки) n
квадрантов, где n-порядок
характеристического уравнения.
Характеристический полином:
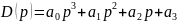
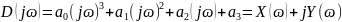
Вещественная функция Михайлова:
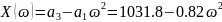
Мнимая функция Михайлова:
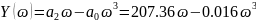
Построим годограф Михайлова:
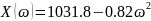
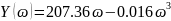
«Таблица для построения годографа Михайлова»
|
|
|
0 |
1031,8 |
0 |
10 |
949,8 |
2057,6 |
20 |
703,8 |
4019,2 |
30 |
293,8 |
5788,8 |
40 |
-280,2 |
7270,4 |
50 |
-1018,2 |
8368 |
60 |
-1920,2 |
8985,6 |
70 |
-2986,2 |
9027,2 |
80 |
-4216,2 |
8396,8 |
90 |
-5610,2 |
6998,4 |
100 |
-7168,2 |
4736 |
110 |
-8890,2 |
1513,6 |
120 |
-10776,2 |
-2764,8 |
130 |
-12826,2 |
-8195,2 |
Пример расчета:
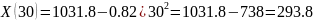
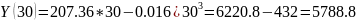
VIII. Построение афх разомкнутой сау.
Частотная передаточная функция разомкнутой системы имеет вид:
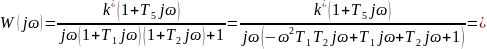
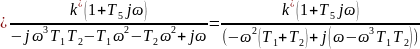
Домножим на комплексно-сопряженное знаменателю число:
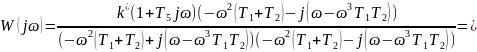
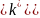
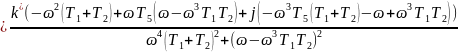
Разделим на вещественную и мнимую части:
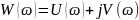
Вещественная часть:
Мнимая часть:
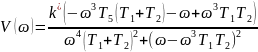
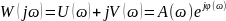
Подставим известные
нам величины:
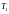 ,
,
,
,
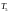 ,
,
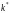 ;
;
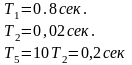
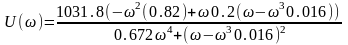
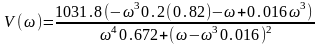
«Данные для построения АФХ разомкнутой системы»
|
|
|
0,5 |
-552,183 |
-1698,889 |
1,5 |
-265,083 |
-167,649 |
2,5 |
-131,807 |
10,297 |
5 |
-42,090 |
42,090 |
10 |
-14,356 |
25,963 |
20 |
-6,579 |
12,293 |
30 |
-4,604 |
7,060 |
40 |
-3,525 |
4,406 |
50 |
-2,779 |
2,895 |
60 |
-2,228 |
1,979 |
70 |
-1,812 |
1,399 |
80 |
-1,493 |
1,018 |
90 |
-1,246 |
0,760 |
100 |
-1,052 |
0,580 |
110 |
-0,898 |
0,452 |
120 |
-0,773 |
0,358 |
130 |
-0,672 |
0,288 |
140 |
-0,589 |
0,234 |
150 |
-0,520 |
0,193 |
160 |
-0,462 |
0,161 |
170 |
-0,414 |
0,136 |
180 |
-0,372 |
0,115 |
190 |
-0,336 |
0,099 |
200 |
-0,305 |
0,085 |
210 |
-0,278 |
0,074 |
220 |
-0,254 |
0,065 |
230 |
-0,234 |
0,057 |
240 |
-0,215 |
0,050 |
250 |
-0,199 |
0,045 |
Пример расчета:
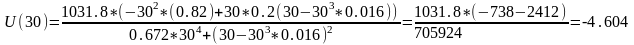
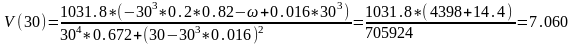
АЧХ:
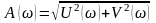
ФЧХ:
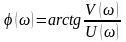

 (Гц)
(Гц)
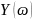
 (Гц)
(Гц)