VII. Исследование сау на устойчивость.

1. Проверка сау на устойчивость по методу Гурвица.

Чтобы САУ была устойчивой, необходимо и достаточно, чтобы все определители Гурвица имели одинаковые знаки со знаком первого коэффициента 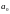характеристического уравнения.

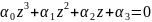
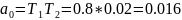
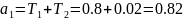
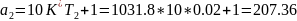
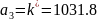
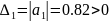
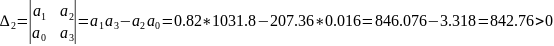
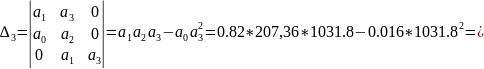
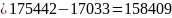> 0

Согласно критерию Гурвица, САУ устойчива.

Проверка САУ на устойчивость по методу Найквиста.

1. Проверка сау на устойчивость по методу Найквиста.

Критерий Найквиста позволяет судить об устойчивости замкнутой системы по виду АФХ разомкнутой системы.

Передаточная функция разомкнутой цепи нашей системы:

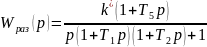
Критерий Найквиста:

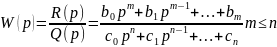
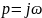
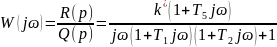
Умножим числитель и знаменатель на выражение, комплексно-сопряженное знаменателю:

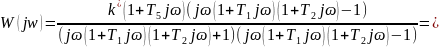
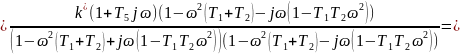
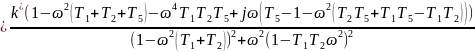
Разделим данное выражение на мнимую и комплексную части:

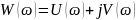
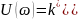
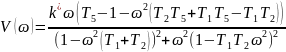
Подставим известные нам величины:

(Гц)
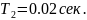
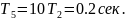
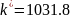
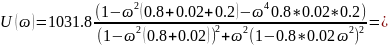
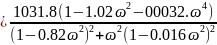
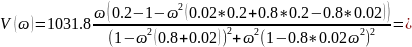
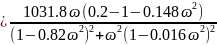
0	1031,800	0
0,5	873,249	-471,154
1,5	-482,326	-459,795
2,5	-257,037	-104,275
5	-70,245	-15,507
10	-20,802	-3,566
20	-7,996	-1,169
30	-5,137	-0,620
40	-3,772	-0,376
50	-2,908	-0,244
60	-2,301	-0,165
70	-1,856	-0,116
80	-1,521	-0,084
90	-1,264	-0,063
100	-1,065	-0,048
110	-0,907	-0,037
120	-0,780	-0,030
130	-0,677	-0,024
140	-0,593	-0,019
150	-0,523	-0,016
160	-0,465	-0,013
170	-0,415	-0,011
180	-0,373	-0,010
190	-0,337	-0,008
200	-0,306	-0,007
210	-0,279	-0,006
220	-0,255	-0,005
230	-0,234	-0,005
240	-0,216	-0,004
250	-0,199	-0,004

Пример расчета:

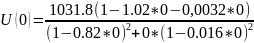
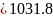
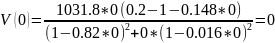
3. Проверка сау на устойчивость по методу Рауса.

Заполним таблицу Рауса. Коэффициенты таблицы определяем согласно формулам:

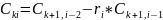
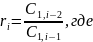
«Таблица Рауса»

knri	Строки	Столбцы
		1	2
…	1	C11=0.016	C21=207.36
…	2	C12=0.82	C22=1031.8
r3=0.02	3	C13=186.72	C23=0
r4=0.004	4	C14=1031.8	C24=0

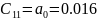
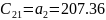
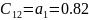
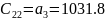
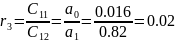
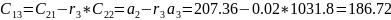
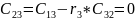
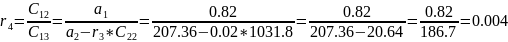
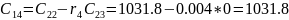
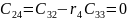
Чтобы САУ была устойчива, необходимо и достаточно, чтобы коэффициенты первого столбца таблицы Рауса имели тот же знак, что и .

Так как 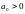, то нужно чтобы , , , .

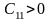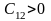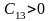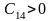Все коэффициенты первого столбца положительны, поэтому правых корней нет и, согласно критерию Рауса, САУ устойчива.