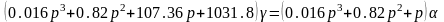VII. Определение параметров системы по наибольшей степени устойчивости.

Т₁= 0.8 cек; Т₅=10 Т₂=0.2 cек; k*=1031.8

a₀z³ + a₁z² + a₂z + a₃ = 0

Смещенное уравнение имеет вид:

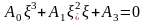, где

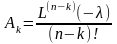; k = 0,1,2,3…, n = 3;

; ; ;

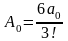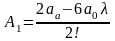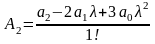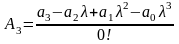
Так как уравнение третьего порядка воспользуемся критерием Вышнеградского, условием апериодической степени устойчивости будет , условием колебательной степени устойчивости будет

1. Определение апериодической степени устойчивости:

T₁=0.8 сек.

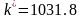
T₅=10T₂=0.2 сек.

;

;

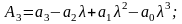
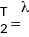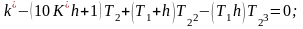
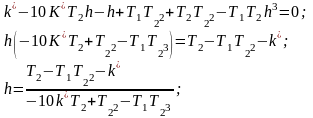
Подставим :

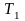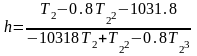
_{Пример расчета h при T2=0.02}

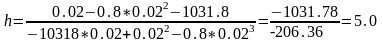
сек.	h		I
0,01	10,0	4,4
0,02	5,0	4,0
0,03	3,3	3,6
0,04	2,5	3,3
0,05	2,0	3,0
0,06	1,7	2,7
0,07	1,4	2,4
0,08	1,2	2,1
0,09	1,1	1,9
0,1	1,0	1,6
0,11	0,9	1,4
0,12	0,8	1,1
0,13	0,8	0,9
0,14	0,7	0,7
0,15	0,7	0,5
0,16	0,6	0,3
0,17	0,6	0,0
0,18	0,6	-0,2
0,19	0,5	-0,4
0,2	0,5	-0,5
0,21	0,5	-0,7
0,22	0,5	-0,9
0,23	0,4	-1,1
0,24	0,4	-1,3
0,25	0,4	-1,4
0,26	0,4	-1,6
0,27	0,4	-1,8
0,28	0,4	-1,9
0,29	0,3	-2,1
0,3	0,3	-2,2

2. Определение колебательной степени устойчивости:

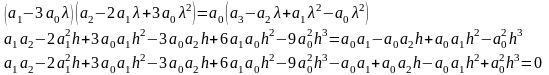
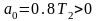
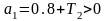
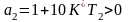
Подставим значения коэффициентов a:

+

+ -

-

Раскроем скобки

+

+ = 0

Приведем подобные

+

+

3.Определение параметров линейной системы по наименьшей квадратичной интегральной оценке качества

,

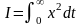где

x– отклонение регулируемой величины от ее нового значения. Оптимальными являются параметры системы, обеспечивающие min интеграла.

Пусть уравнение статической системы, где задающее воздействие постоянно, будет иметь вид:

(a₀ pⁿ + a₁p^n-1 + … + a_n-1 p + a_n) * x₁=

= (b₀ p^m + b₁p^m-1 + … + b_m-1 p + b_m) * 1

Отклонение регулируемой величины от ее нового установившегося значения в любой момент времени переходного процесса, равно

,

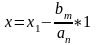где

х₁ – текущее значение регулируемой величины, отсчитываемое от ее старого значения, установившегося при единичном скачке.

При единичной оценке при этих условиях АА

Красовский предложил формулу:

,

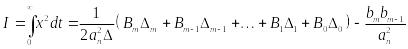где _n – определитель n-ого порядка.

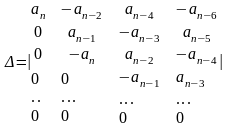
Определитель _k получается из матрицы заменой (m - k + 1) столбца столбцом

a_n-1

a_n

0

0

Коэффициенты В_k составляются из коэффициентов операторов многочлена правой части уравнения системы:

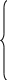
B_m = b²_m

B_m-1 = b²_m-1 – 2b_m*b_m-2

B_m-2 = 2b_m-2 – 2b_m-1*b_m-3 + 2*b_m*b_m-4

…

B_k = b²_k – 2*b_k+1*b_k-1 + 2*b_k+2*b_k-2 +…+ 2(-1)^k*b_m*b_2k-m

B₀ = b²₀

Для вычисления интеграла применяем формулу:

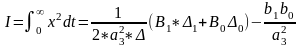
Найдем определители , , , для этого проведем выбор параметров:

;

;

;

;

;

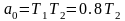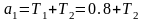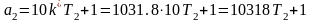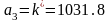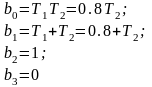
Пример расчета:

При Т₂=0.02 сек.

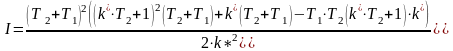
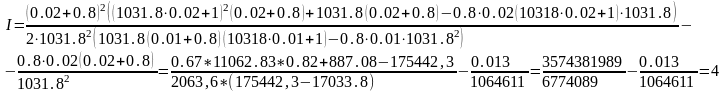
Первое пересечение достигается в точке I= 4 при T₂=0.02

Используем коэффициенты этого метода:

;

;

;

;

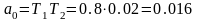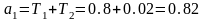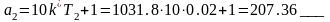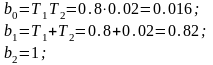
Уравнение в общем виде будет выглядеть:

;