Санкт-Петербургский Государственный

Университет Телекоммуникаций

им.проф. М.А.Бонч-Бруевича

кафедра: Автоматизации предприятий связи (АПС)

Курсовая работа по дисциплине

“Теория автоматического управления”

на тему:

“ Исследование масштабной следящей системы”

Работу выполнил

студент гр. ТСС-96:

Атаев. М.

Работу проверила:

проф. Верхова Г.В.

Санкт-Петербург 2012

Содержание:

I. Исходные данные 3

II. Следящая система

1. Схема следящей системы 3

2. Краткое описание системы 3

III. Уравнения звеньев системы.

Составление структурной схемы системы

1. Уравнение управляемого объекта с двигателем 4

2. Уравнение обратной связи 4

3. Уравнение датчика рассогласования 4

4. Уравнение потенциометра 4

5. Уравнение дифференциального контура 5

6. Уравнение усилителя и цепи возбуждения генератора 5

7. Уравнение цепи якорей генератора и двигателя 6

8. Единое уравнение системы 6

9. Передаточные функции звеньев 7

10. Структурная схема следящей системы 7

IV. Приведение системы к единому уравнению.

Составление передаточной функции замкнутой системы и её разомкнутой цепи 7

V. Получение уравнения статики системы и

его использование ..9

VI. Проверка системы на устойчивость. Критерий Вышнеградского ..9

VII. Определение параметров линейной САУ по наибольшей степени устойчивости.

1. Определение апериодической степени устойчивости…………………………….11

2. Определение колебательной степени устойчивости………………………………12

3. Определение параметров линейной системы автоматического регулирования по наименьшей квадратичной интегральной оценке качества 13

VIII. Исследование САУ на устойчивость

1. Проверка САУ на устойчивость по методу Гурвица 16

2. Проверка САУ на устойчивость по методу Найквиста 16

3. Проверка САУ на устойчивость по методу Рауса 19

4. Проверка САУ на устойчивость по методу Михайлова 20

IX. Построение АФХ разомкнутой САУ…………………………………………………..21

X. Построение ЛФЧХ разомкнутой системы 23

XI. Построение ЛАЧХ разомкнутой системы 25

XII. Вывод 28

I. Исходные данные

T1,сек.	K0	α(t),рад.	γст	α
0.8	1	1.5	10	3

II. Следящая система

1. Схема следящей системы.

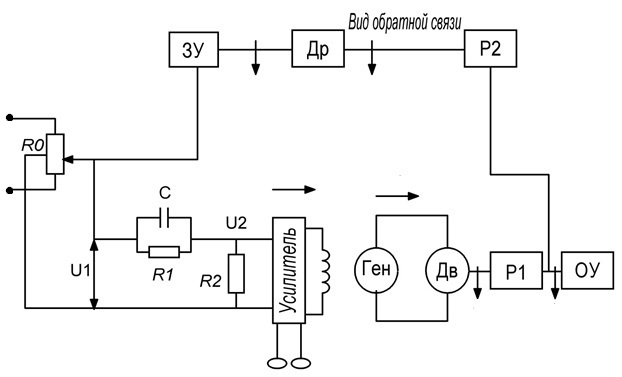
α α₁

I3 I4

ɷ 𝛽

ЗУ-задающее устройство P1,P2-редуторы

R₀-потенциометр УО-управляемый объект

Ген.-генератор ДР-датчик рассогласования

Дв.-двигатель

2. Описание системы.

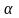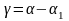Система предназначена для слежения в постоянном масштабе вала управляемого объекта за задающим валом. Механический дифференциал выполняет функцию датчика рассогласования, сравнивая углы поворота вала задающего устройства и вала обратной связи _1, полученное рассогласование с помощью потенциометра преобразуется в напряжение U₁, которое подается на вход дифференцируемого контура состоящего из емкости и сопротивления R₁ и R₂.

Усиленный усилителем ток I₃ поступает на обмотку возбуждающего генератора, цепь якоря которого последовательно соединена с цепью якоря двигателя постоянного тока с независимым возбуждением.

Двигатель через редуктор P₁ поворачивает вал управляемого объекта на угол β = k₀*α . Т.к. датчик рассогласования должен сравнивать величины одного масштаба, в цепь обратной связи включен редуктор P₂, задача которого изменение масштаба угла β в 1/k₀ раз.