5.Схема алгоритма выполнения задания 2
Для выполнения задания 2 выпишем в развернутой форме интерполяционные многочлены Лагранжа и Ньютона
.
Отсюда получаем
(0.5)
(0.7)
где
вычисляются по формулам типа (0.1), (0.3).
По условию
задания 2
Поэтому
из формул (0.5), (0.6) имеем
(0.8)
Таким образом, алгоритм выполнения задания 2 имеет следующую схему
1. Вводим заданные
узлы
и значения табличной функции
2. Вычисляем коэффициенты интерполяционного многочлена Лагранжа по формулам
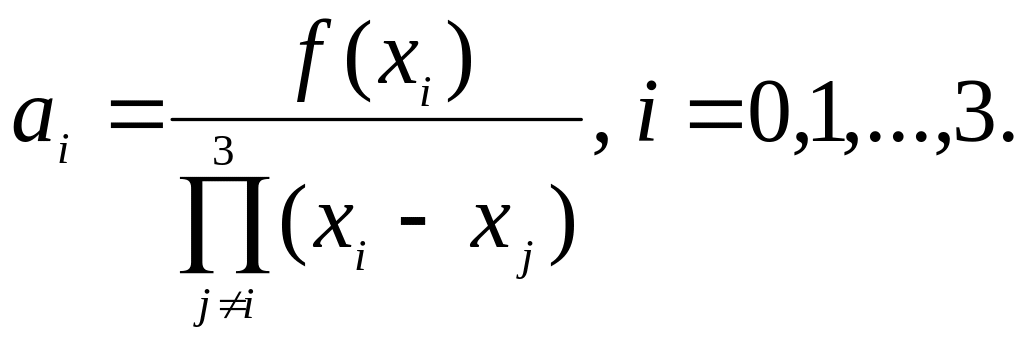
По этим коэффициентам выписываем интерполяционный многочлен Лагранжа
3. Вычисляем коэффициенты интерполяционного многочлена Ньютона по формулам
.
А разделенные
разности
вычисляем по формулам (*). По этим
коэффициентам выписываем интерполяционный
многочлен Ньютона
.
4. Вычисляем
и
по формулам (0.8). Затем вычисляем
6.Программа выполнения задания 1
uses crt;{$F+}
const n=5;
type vect=array[0..n] of real;
fnc=function(x:real):real;
const xn:vect=(0.5,0.8,1.0,1.2,1.4,1.5);
var i,j,k:integer;a,b:vect;
x,lgr,ntn,d1,d2:real;
function f1(x:real):real;
begin
if abs(x)<=1 then f1:=x*sqrt(1-x*x)
else f1:=sin(x)*cos(x)
end;
procedure lagr(n:integer;xx:vect;x:real;f:fnc; var a:vect;var lgr:real);
var i,j:integer;
s,p:real;
begin
for i:=0 to n do
begin
p:=1;
for j:=0 to n do if j<>i then p:=p*(xx[i]-xx[j]);
a[i]:=f(xx[i])/p
end;
s:=0;
for i:=0 to n do
begin
p:=1;
for j:=0 to n do if j<>i then p:=p*(x-xx[j]);
s:=s+a[i]*p
end;
lgr:=s
end;
procedure nton(n:integer;xx:vect;x:real;f:fnc; var b:vect;var ntn:real);
var i,j:integer;
s,p:real;
begin
b[0]:=f(xx[0]);
for i:=1 to n do
begin
s:=0;
for j:=0 to i do
begin
p:=1;
for k:=0 to i do
if k<>j then p:=p*(xx[j]-xx[k]);
s:=s+f(xx[j])/p
end;
b[i]:=s
end;
s:=b[0];
for i:=1 to n do
begin p:=1;
for j:=0 to i-1 do p:=p*(x-xx[j]);
s:=s+b[i]*p
end;
ntn:=s;
end;
begin clrscr; writeln; x:=0.9;
lagr(n,xn,x,f1,a,lgr); writeln('koefic Lagranga');
for i:=0 to n do writeln('a',i,'=',a[i]:11:2);readkey;writeln;
writeln;
nton(n,xn,x,f1,b,ntn); writeln('koefic Ntona');
for i:=0 to n do writeln('b',i,'=',b[i]:11:2);readkey;writeln;
writeln('f(',x:3:1,')=',f1(x):7:4,' L(',x:3:1,')=',lgr:7:4,
' N(',x:3:1,')=',ntn:7:4 ); d1:=abs(f1(x)-lgr); d2:=abs(f1(x)-ntn);
writeln('d1=',d1:8,' d2=',d2:8);
readkey
end.
По этой программе получены следующие значения
a=-4.58,47.62,0.00,100.52,-38.77,6,72
b=0.43,0.16,-5.11,21.91,-55.03,111.50
f(0.9)=0.3923 L(0.9)=0.0706 N(0.9)=0.0706 d1=d2=0.3219