Требования к оформлению лабораторной работы.

Лабораторная работа должна содержать:

1. Курс, группа, фамилия, имя, отчество и номер варианта;

2. Тема лабораторной работы;

3. Четко сформулированные условия лабораторных заданий;

4. Краткое описание применяемых методов;

5. Схема алгоритм выполнения каждого задания;

6. Программа выполнения на ЭВМ каждого задания,

составленную по схеме алгоритма пункта 5;

7. Результаты каждого задания в виде таблиц;

8. Краткие выводы о результатах.

Если не соблюдены приведенные здесь требования, то

лабораторная работа не принимается к зачету.

Образец выполнения лабораторной работы №1

Лабораторная работа №1

1.3 Курс, 5 группа, Магомедов Магомед Магомедович

Вариант № 0

2. Тема: Интерполирование функции одной переменной

3. Задание 1

Для функции составить интерполяционные многочлены Лагранжа L и Ньютона N, используя значения в узлах, 0.5, 0.8, 1.0, 1.2, 1.4, 1.5. Найти их значения и значение функции в точке Сравнить все три полученные значения. Заполнить таблицу вида

Интерполяционные многочлены Лагранжа и Ньютона

		Погрешности
		=…
		=…

В коэффициентах многочленов сохранять по 2 десятичных знака, в значениях и - по 4 десятичных знака, погрешность записать в форме с плавающей точкой.

Задание 2

Для функции заданной таблично

	-0.2	0	0.1	0.2
	0.982	1.343	0.871	0.467

составить интерполяционные многочлены Лагранжа L и Ньютона N, используя значения во всех данных в таблице узлах. Найти полагая а) б) ,где =0. Заполнить таблицу вида

Интерполяция табличной функции

В коэффициентах сохранять по 2 десятичных знака, в - по 4 десятичных знака, записать в форме с плавающей точкой.

4.Краткое описание применяемого метода.

Поскольку узлы различные, то согласно теории существует

единственный интерполяционный многочлен. По формуле (1)

этот интерполяционный многочлен в форме Лагранжа имеет вид

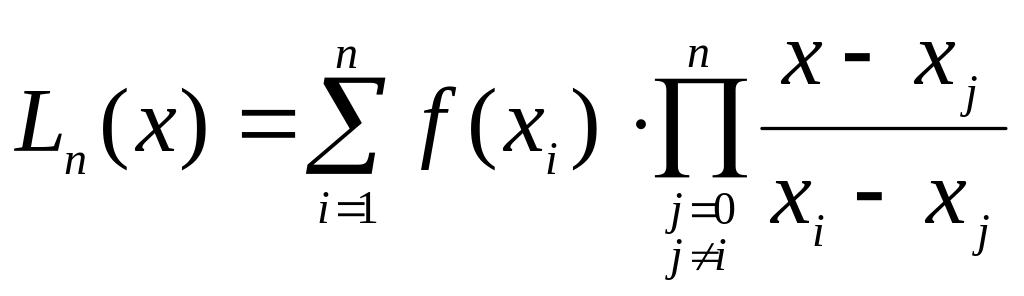а в форме Ньютона по формуле (2)- вид

где заданные узлы интерполяции, а разделенная разность порядка , которая определяется по формуле (*). В задании 1 n=5, в задании 2 n=4. Из этих формул следует, чтобы построить интерполяционные многочлены Лагранжа и Ньютона необходимо вычислить их коэффициенты.