ДАГЕСТАНСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ

Абдурагимов Э.И.

ЛАБОРАТОРНАЯ РАБОТА

ИНТЕРПОЛЯЦИЯ ФУНКЦИИ ОДНОЙ ПЕРЕМЕННОЙ

Пособие содержит краткие теоретические сведения и варианты лабораторных заданий по вычислительному практикуму по теме: "Интерполяция функции одной переменной". В нем приводится также образец выполнения нулевого варианта, аналогичного вариантам, которые должны выполнить студенты.

Махачкала 2007

Краткие теоретические сведения.

1.Постановка задачи интерполирования.

Пусть на отрезке [a,b] заданы n+1 точки , которые называются узлами интерполяции, и значения некоторой функции в этих точках . Требуется построить функцию (интерполирующая функция), принадлежащую известному классу и имеющую в узлах интерполяции те же значения, что и , т.е. такую, что

Геометрически это означает, что нужно найти кривую некоторого определенного типа, проходящую через заданную систему точек .

Полученную интерполяционную формулу обычно используют для приближенного вычисления значений данной функции для значений аргумента х, отличных от узлов интерполяции. Такая операция называется интерполированием функции .

В такой общей постановке задача может иметь бесчисленное множество решений или совсем не иметь их. Однако эта задача становится однозначной, если вместо произвольной функции искать полином степени не выше , удовлетворяющий условиям (1), т.е. такой, что .

1. Интерполяционный многочлен Лагранжа.

Если узлы различны, то существует единственный интерполяционный многочлен степени . Его можно записывать в различных формах. Рассмотрим интерполяционный многочлен Лагранжа и Ньютона. В форме Лагранжа интерполяционный многочлен имеет вид 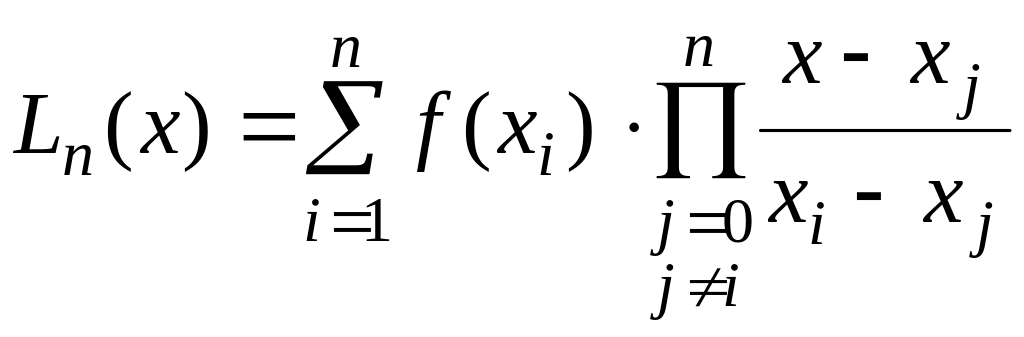(1)

Например,

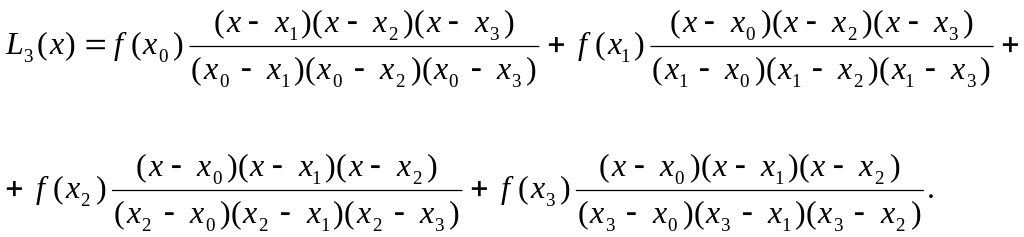
2. Разделенные разности. Интерполяционный многочлен Ньютона.

Чтобы ознакомиться с интерполяционным многочленом в форме Ньютона, введем в рассмотрение понятие разделенная разность. Значения функции в узлах называются разделенными разностями нулевого порядка. Числа вида называются разделенными разностями первого порядка.

Разделенная разность -го порядка определяется через разделенные разности -го порядка по реккурентной формуле .

Разделенную разность -го порядка ( ) можно выразить через по следующей формуле (см. например [2]:

. (*)

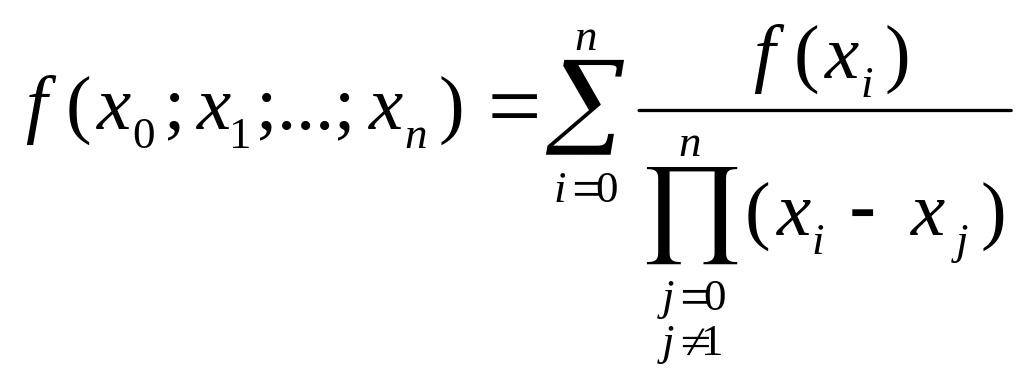Например,

.

Из (4) следует, что разделенная разность – симметричная функция своих аргументов. С помощью разделенных разностей интерполяционный многочлен в форме Ньютона можно записать следующим образом:

(2)

3. Погрешность интерполяции

Пусть - интерполяционный многочлен, построенный для функции по узлам интерполяции из отрезка по формуле (1) или (2). Тогда можно написать приближенное равенство .

Разность , выражающая погрешность интерполяции, называется остаточным членом и обозначается . Его можно записать (см. например [3]) в виде

, (3)

где , а - некоторая неизвестная точка, или с помощью разделенных разностей в виде

(4)

Остаточный член в форме (3) используют в том случае, когда . В этом случае

, (5)

где .

Если же не принадлежит , то пользуются остаточным членом в форме (4).

Пример. С какой точностью можно вычислить с помощью интерполяционной формулы Лагранжа (1) для функции , выбрав узлы интерполирования 100, 121, 144?

Решение. Имеем . Отсюда при . На основании формулы (5), получаем .

4. Замечания об интерполяционных формулах Лагранжа и Ньютона

Итак, мы имеем две различные записи одного и того же интерполяционного многочлена в форме Лагранжа и в форме Ньютона. У интерполяционного многочлена Лагранжа (1) видна явная его зависимость от каждого значения . Такая зависимость позволяет, например, вычислять значения ряда различных функций в фиксированной точке по заданной системе узлов . Для этой цели необходимо сначала вычислить коэффициенты Лагранжа в фиксированной точке и запомнить, затем для различных функций можно вычислить значения соответствующих интерполяционных многочленов по формуле (1).

Однако, если менять , то интерполяционный многочлен Лагранжа требуется строить заново. В этом состоит его недостаток.

Из формулы (2) видно, что при изменении степени у интерполяционного многочлена Ньютона требуется только добавить или отбросить соответствующее число стандартных слагаемых. Это обстоятельство можно использовать на практике при составлении таблицы значений заданной функции.

5. Конечные разности.

Конечные разности являются рабочим аппаратом при изучении функций, заданных таблицей значений в равноотстоящих точках и применяются в вычислениях с такими функциями.

Пусть узлы некоторой таблицы расположены на равных расстояниях: , называют шагом таблицы. Обозначим через значение функции в узле . Разность называют разностью первого порядка; в зависимости от обстановки эту величину обозначают как разность вперед , разность назад , центральную разность . Таким образом,

Разности высших порядков образуют при помощи рекуррентных соотношений:

Разности -го порядка можно выразить через значения функции следующим образом ( ): .

Здесь при четном -целое, при нечетном -полуцелое. Например: ; ;

Разделенная и конечная разности связаны соотношением ( ):

.