2.3 Структурная схема двухдвигательного асинхронного электропривода с преобразователем частоты

Известная [4], структурная схема двухдвигательного электропривода представлена на рисунке 2.4.

Рисунок 2.4 - Структурная схема двухдвигательного асинхронного электропривода

Линеаризованная структурная схема (см. рисунок 2.4) состоит из двух идентичных асинхронных электродвигателей с фазным ротором, где роторные связи имитировались инерционно-дифференцирующим звеном от разности углов рассогласования. Инерционно-дифференцирующее звено представляется в следующем виде [24]:

. (2.21)

Введение такого звена в математическую модель двухдвигательного асинхронного электропривода дает возможность осуществить синхронизацию скоростей при небольших разностей нагрузок двигателей системы.

Однако для осуществления возможности согласования скоростей при большей разностей нагрузок двигателей системы предлагается разработанная структурная схема (см. рисунок 2.5) двухдвигательного асинхронного электропривода с двигателями с короткозамкнутым ротором. Следует отметить, что структурная схема двухдвигательного электропривода с преобразователем частоты составлена согласно структурной схемы однодвигательного электропривода с системой ПЧ (см. рисунок 2.2).

Обратные связи по рассогласованию скоростей предложены на основании [Т]

Рисунок 2.5 - Структурная схема двухдвигательного электропривода по системе ПЧ-АД с обратной связью по скорости

Как видно из рисунка 2.5. двухдвигательный асинхронный электропривод с преобразователем частоты состоит из двух асинхронных двигателей с короткозамкнутым ротором, двух преобразователей частоты и двух регуляторов скорости. Каждый асинхронный двигатель с преобразователем частоты имеет свою обратную связь по скорости с коэффициентами обратной связи К_ос1 и К_ос2 . Для обеспечения согласованного вращения двигателей введена обратная связь с коэффициентом обратной отрицательной связи К_оос. Скорости первого ∆ω₁ и второго ∆ω₂ двигателей суммируются с учетом коэффициентов К₁ и К₂ в устройстве ∑₁, выходной сигнал ∆U_pc =K_оос(К₁∆ω₁+ К₂∆ω₂), с которого подается в устройство ∑_с, где поданный сигнал ∆U_сc сравнивают с задающим сигналом управления ∆U_зc, после чего полученный сигнал подается на вход системы ПЧ-АД с обратными связями по скорости.

2.4. Оптимизация структуры и устойчивость движения двухдвигательного асинхронного электропривода с системой пч-ад

Как указывалось выше, двухдвигательный асинхронный электропривод с системой ПЧ-АД (см. рисунок 2.5) состоит из двух асинхронных двигателей, работающих на один вал. Известно, что при работе двух двигателей на один вал нагрузка будет распределена поровну только в том случае, когда их механические характеристики совпадают. Практически достичь этого невозможно [9]. Это объясняется тем, что согласно действующему ГОСТу допуск на скольжение при изготовлении асинхронных двигателей составляет +25%.

Поэтому двигатели одного и того же типоразмера могут иметь различные скольжения при номинальной нагрузке на валу. Если номинальные моменты двух идентичных двигателей обозначить через М_н­, а их фактические скольжения соответствующие этому моменту S₁ и S_­­_2­, то при работе этих двигателей на один вал они будут развивать моменты, равные

, (2.22)

, (2.23)

где S общее скольжение, с которым будут работать двигатели. Учитывая, что суммарный момент, развиваемый двигателем при нормальной их загрузке, равен

, (2.24)

откуда

. (2.25)

Таким образом, распределение суммарной нагрузки между двумя двигателями, работающими на один вал, имеют идентичные характеристики, а напряжения, подводимые на зажимы двигателей, одинаковы. Поэтому данное условие учитывается в дальнейшем при оптимизации структурной схемы модели двухдвигательного асинхронного электропривода (ДАЭП с ПЧ-АД). Предполагаемая структурная схема модели ДАЭП с ПЧ-АД представлена на рисунке 2.6.

Рисунок 2.6 - Структурная схема модели двухдвигательного асинхронного электропривода (ДАЭП с ПЧ-АД)

Для сравнения предложенной структурной схемы модели ДАЭП с ПЧ-АД с другими оптимизированными структурами, рассмотрим устойчивость движения ДАЭП с ПЧ-АД и переходной процесс суммирующего сигнала скоростей двигателей этого двухдвигательного асинхронного электропривода. Устойчивость движения ДАЭП с ПЧ-АД будем рассматривать на основании характеристического уравнения передаточной функции ДАЭП.

Для получения передаточной функции ДАЭП составляется программа в системе MATLAB. Полученная программа в системе MATLAB представлена на рисунке 2.7.

>> n=[0.178];

>> m=[1 0];

>> W1=tf(n,m)

Transfer function: (передаточная функция)

0.178

-----

s

>> n2=[28];

>> m2=[0.05 1];

>> W2=tf(n2,m2)

Transfer function: (передаточная функция)

28

----------

0.05 s + 1

>> G1=W1*W2

Transfer function: (передаточная функция)

4.984

------------

0.05 s^2 + s

>> Q1=feedback(G1,[1])

Transfer function: (передаточная функция)

4.984

--------------------

0.05 s^2 + s + 4.984

>> n3=[7.28];

>> m3=[0.001 1];

>> W3=tf(n3,m3)

Transfer function: (передаточная функция)

7.28

-----------

1. s + 1

>> n4=[0.15 1];

>> m4=[0.4 0];

>> W4=tf(n4,m4)

Transfer function: (передаточная функция)

0.15 s + 1

----------

0.4 s

>> C1=Q1*W3*W4

Transfer function: (передаточная функция разомкнутой

системы ПЧ - АД)

5.443 s + 36.28

---------------------------------------------

2e-005 s^4 + 0.0204 s^3 + 0.402 s^2 + 1.994 s

>> Wc1=feedback(C1,[0.3])

Transfer function: (передаточная функция замкнутой

системы ПЧ - АД)

5.443 s + 36.28

-----------------------------------------------------

2e-005 s^4 + 0.0204 s^3 + 0.402 s^2 + 3.626 s + 10.89

>> Wc2=Wc1

Transfer function:

5.443 s + 36.28

-----------------------------------------------------

2e-005 s^4 + 0.0204 s^3 + 0.402 s^2 + 3.626 s + 10.89

>> Dv=parallel(Wc1,Wc2)

Transfer function: (передаточная функция разомкнутого двухдвигательного электропривода)

0.0002177 s^5 + 0.2235 s^4 + 5.856 s^3 + 68.64 s^2 + 381.6 s

+ 789.9

----------------------------------------------------------------

4e-010 s^8 + 8.16e-007 s^7 + 0.0004322 s^6 + 0.01655 s^5

+ 0.31 s^4 + 3.36 s^3 + 21.9 s^2 + 78.95 s + 118.5

>> h1=[0.2];

>> z1=[1];

>> Woc=tf(h1,z1)

Transfer function:

0.2

>> Wc=feedback(Dv,Woc,-1)

Transfer function: (передаточная функция замкнутого двухдвигательного электропривода)

0.0002177 s^5 + 0.2235 s^4 + 5.856 s^3 + 68.64 s^2 + 381.6 s

+ 789.9

---------------------------------------------------------------

4e-010 s^8 + 8.16e-007 s^7 + 0.0004322 s^6 + 0.01659 s^5

+ 0.3547 s^4 + 4.531 s^3 + 35.63 s^2 + 155.3 s + 276.5

>> P = [4e-10 8.16e-7 0.0004322 0.01659 0.3547 4.531 35.63 155.3 276.5]; (характеристическое уравнение)

>> r = roots(P)

Корни характеристического уравнения:

r =

1.0e+003 *

-1.0103

-0.9900

-0.0068 + 0.0126i

-0.0068 - 0.0126i

-0.0073 + 0.0071i

-0.0073 - 0.0071i

-0.0063

-0.0052

Рисунок 2.7 - Программа определения устойчивости ДАЭП с системой ПЧ-АД

Из представленной программы (см. рисунок 2.7) видно, что движение ДАЭП с системой ПЧ-АД устойчивое, так как корни характеристического уравнения (r) с отрицательной вещественной частью. Переходной процесс суммирующего сигнала S­_∑ показан на рисунке 2.8.

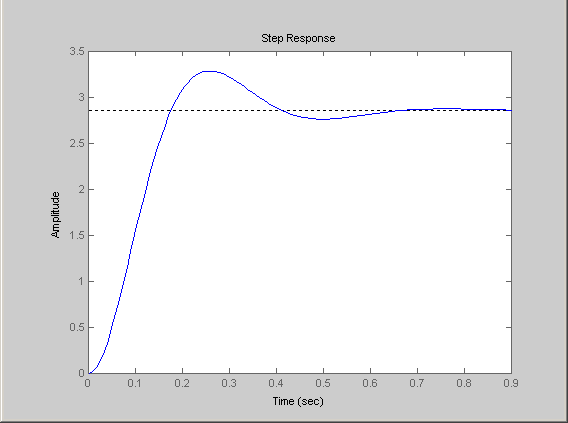
Рисунок 2.8 - Переходной процесс суммирующего сигнала S­_∑ ДАЭП с ПЧ-АД

Однако, структурная схема модели ДАЭП с ПЧ-АД с обратной связью по скорости (см. рисунок 2.6) может быть представлена без обратных связей по скорости системы ПЧ-АД (см. рисунок 2.9).

Рисунок 2.9 - Структурная схема модели ДАЭП с ПЧ-АД без обратных связей по скорости

Это связано с тем, что предложенная обратная связь суммирующего сигнала скоростей двигателей подается на вход ДАЭП, обеспечивая при этом соответствующую устойчивость движения ДАЭП с ПЧ-АД без обратных связей по скорости. Устойчивость такой системы рассмотрим так же по корням характеристического уравнения данной модели.

Программа определения устойчивости движения дается на рисунке 2.10.

>> n=[0.178];

>> m=[1 0];

>> W1=tf(n,m)

Transfer function:(передаточная функция)

0.178

-----

s

>> n2=[28];

>> m2=[0.05 1];

>> W2=tf(n2,m2)

Transfer function: (передаточная функция)

28

----------

0.05 s + 1

>> G1=W1*W2

Transfer function:

4.984

------------

0.05 s^2 + s

>> Q1=feedback(G1,[1])

Transfer function: (передаточная функция)

4.984

--------------------

0.05 s^2 + s + 4.984

>> n3=[7.28];

>> m3=[0.001 1];

>> W3=tf(n3,m3)

Transfer function: (передаточная функция)

7.28

-----------

0.001 s + 1

>> n4=[0.15 1];

>> m4=[0.4 0];

>> W4=tf(n4,m4)

Transfer function:

0.15 s + 1

----------

0.4 s

>> C1=Q1*W3*W4

Transfer function: (передаточная функция системы ПЧ-АД без обратной связи по скорости)

5.443 s + 36.28

---------------------------------------------

2e-005 s^4 + 0.0204 s^3 + 0.402 s^2 + 1.994 s

>> Wc1=C1

Transfer function:

5.443 s + 36.28

---------------------------------------------

2e-005 s^4 + 0.0204 s^3 + 0.402 s^2 + 1.994 s

>> Wc2=C1

Transfer function: (передаточная функция)

5.443 s + 36.28

---------------------------------------------

2e-005 s^4 + 0.0204 s^3 + 0.402 s^2 + 1.994 s

>> Wc=parallel(Wc1,Wc2)

Transfer function: (передаточная функция ДАЭП)

0.0002177 s^5 + 0.2235 s^4 + 5.856 s^3 + 50.87 s^2 + 144.7 s

------------------------------------------------------------------------

4e-010 s^8 + 8.16e-007 s^7 + 0.0004322 s^6 + 0.01648 s^5 + 0.2429 s^4

+ 1.603 s^3 + 3.974 s^2

>> h1=[0.2];

>> z1=[1];

>> Woc=tf(h1,z1)

Transfer function: (передаточная функция)

0.2

>> Wd=feedback(Wc,Woc,-1)

Transfer function: (передаточная функция ДАЭП с обратной связью по суммирующему сигналу скоростей)

0.0002177 s^5 + 0.2235 s^4 + 5.856 s^3 + 50.87 s^2 + 144.7 s

-------------------------------------------------------------------------

4e-010 s^8 + 8.16e-007 s^7 + 0.0004322 s^6 + 0.01652 s^5 + 0.2876 s^4

+ 2.774 s^3 + 14.15 s^2 + 28.93 s

>> P = [4e-10 8.16e-7 0.0004322 0.01652 0.2876 2.774 14.15 28.93];

>> r = roots(P) (корни характеристического уравнения)

r =

1.0e+003 *

-1.0096

-0.9905

-0.0071 + 0.0088i

-0.0071 - 0.0088i

-0.0104

-0.0096

-0.0057

Рисунок 2.10 - Программа определения устойчивости движения

ДАЭП с ПЧ-АД без обратных связей по скорости

Из представленной программы (см. рисунок 2.10) видно, что движение ДАЭП с ПЧ-АД без обратных связей по скорости устойчивое, так как корни характеристического уравнения (r) с отрицательной вещественной частью. Переходной процесс суммирующего сигнала S­_∑ показан на рисунке 2.11.

Рисунок 2.11 - Переходной процесс суммирующего сигнала S­_∑ ДАЭП с ПЧ-АД без обратных связей по скорости

Но указанную выше структуру ДАЭП с ПЧ-АД без обратных связей по скорости (см. рисунок 2.9) можно так же оптимизировать по количеству элементов, т.е. где будет использован один преобразователь частоты и одно корректирующее устройство, с целью обеспечения экономии затрат электроэнергии и надежности работы этого ДАЭП. Структурная схема ДАЭП с системой ПЧ-АД без обратных связей по скорости с одним преобразователем частоты и одним корректирующим устройством представлена на рисунке 2.12.

Рисунок 2.12 - Структурная схема ДАЭП с системой ПЧ-АД без обратных связей по скорости с одним преобразователем частоты и одним корректирующим устройством

Программа определения устойчивости движения дается на рисунке 2.13.

>> n=[0.178];

>> m=[1 0];

>> W1=tf(n,m)

Transfer function:

0.178

-----

s

>> n2=[28];

>> m2=[0.05 1];

>> W2=tf(n2,m2)

Transfer function:

28

----------

0.05 s + 1

>> G1=W1*W2

Transfer function:

4.984

------------

0.05 s^2 + s

>> Q1=feedback(G1,[1])

Transfer function:

4.984

--------------------

0.05 s^2 + s + 4.984

>> Q2=Q1

Transfer function:

4.984

--------------------

0.05 s^2 + s + 4.984

>> Wob=parallel(Q1,Q2)

Transfer function:

0.4984 s^2 + 9.968 s + 49.68

--------------------------------------------------

0.0025 s^4 + 0.1 s^3 + 1.498 s^2 + 9.968 s + 24.84

>> n3=[7.28];

>> m3=[0.001 1];

>> W3=tf(n3,m3)

Transfer function:

7.28

-----------

0.001 s + 1

>> n4=[0.15 1];

>> m4=[0.4 0];

>> W4=tf(n4,m4)

Transfer function:

0.15 s + 1

----------

0.4 s

>> G1=Wob*W3*W4

Transfer function:

0.5443 s^3 + 14.51 s^2 + 126.8 s + 361.7

------------------------------------------------------------------------

1e-006 s^6 + 0.00104 s^5 + 0.0406 s^4 + 0.6033 s^3 + 3.997 s^2 + 9.936 s

>> h1=[0.2];

>> z1=[1];

>> Woc=tf(h1,z1)

Transfer function:

0.2

>> Ws=feedback(G1,Woc,-1)

Transfer function:

0.5443 s^3 + 14.51 s^2 + 126.8 s + 361.7

------------------------------------------------------------------------

1e-006 s^6 + 0.00104 s^5 + 0.0406 s^4 + 0.7122 s^3 + 6.9 s^2 + 35.3 s +72.33

>> P = [1e-6 0.00104 0.0406 0.7122 6.9 35.3 72.33];

>> r = roots(P)

r =

1.0e+003 *

-1.0001

-0.0071 + 0.0087i

-0.0071 - 0.0087i

-0.0106

-0.0094

-0.0057

Рисунок 2.13 - Программа определения устойчивости движения ДАЭП с системой ПЧ-АД без обратной связи по скорости с одним регулятором скорости и с одним преобразователем частоты

Из представленной программы (см. рисунок 2.13) видно, что движение ДАЭП с системой ПЧ-АД без обратных связей по скорости с одним регулятором скорости и с одним преобразователем частоты устойчивое, так как корни характеристического уравнения (r) с отрицательной вещественной частью. Переходной процесс суммирующего сигнала S­_∑ показан на рисунке 2.14.

Рисунок 2.14 - Переходной процесс суммирующего сигнала S­_∑ ДАЭП с ПЧ-АД без обратных связей по скорости