28.Понятие системы случайных величин

Понятие о системе случайных величин

В практических применениях теории вероятностей очень часто приходится сталкиваться с задачами, в которых результат опыта описывается не одной случайной величиной, а двумя или более случайными величинами, образующими комплекс или систему.

Свойства системы нескольких случайных величин не исчерпываются свойствами отдельных величин, ее составляющих: помимо этого, они включают также взаимные связи (зависимости) между случайными величинами. При рассмотрении вопросов, связанных с системами случайных величин, удобно пользоваться геометрической интерпретацией системы.

Например, систему двух случайных величин (X, Y) можно изображать случайной точкой на плоскости с координатами X и Y .

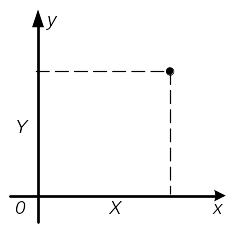
А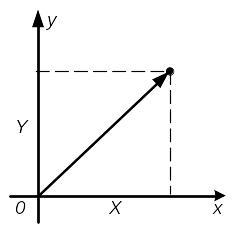 налогично система трех случайных величин может быть изображена случайной точкой в трехмерном пространстве. Часто бывает удобно говорить о системе n случайных величин как о «случайной точке в пространстве n измерений». Часто вместо образа случайной точкой для геометрической интерпретации системы случайных величин пользуются образом случайного вектора. Систему двух случайных величин при этом рассматривают как случайный вектор на плоскости хОу, составляющие которого по осям представляют собой случайных величин Х, Y.

Система трех случайных величин изображается случайным вектором в трехмерном пространстве, система n случайных величин — случайным вектором в пространстве n измерений.

При этом теория систем случайных величин рассматривается как теория случайных векторов.

29.Дайте определение и укажите основные свойства функции распределения системы величин.

F (х,y) = Р ((Х < х)(Y < у))

Функцией распределения системы двух случайных величин (X, Y) называется вероятность совместного выполнения двух неравенств Х < х и Y < у:

при x2 > x1 F (x2, y) ≥ F (x1, y);

при y2 > y1 F (x, y2) ≥ F (x, y1).

1. Функция распределения F (х, у) есть неубывающая функция обоих своих аргументов, т. е.

2. Повсюду на -∞ функция распределения равна нулю: F (x, -∞) = F (-∞, y) = F (-∞, -∞) .В этом свойстве мы наглядно убеждаемся, неограниченно отодвигая влево правую границу квадранта (х → -∞) или вниз его верхнюю границу (у → -∞) или делая это одновременно с обеими границами; при этом вероятность попадания в квадрант стремится к нулю.

3. При одном из аргументов, равном +∞, функция распределения системы превращается в функцию распределения случайной величины, соответствующей другому аргументу:

F (x, +∞) = F1 (х),

F (+∞, у) = F2 (y).

где F1 (х), F2 (y) – соответственно функции распределения случайных величин X и Y.

В этом свойстве функции распределения можно наглядно убедиться, смещая ту или иную из границ квадранта на +∞; при этом в пределе квадранта превращается в полуплоскость, вероятность попадания в которую есть функция распределения одной из величин, входящих в систему.

4. Если оба аргумента равны + ∞, функция распределения системы равна 1:

F (+ ∞, + ∞) =1

Действительно, при х→+∞, у→+∞ квадрант с вершиной (х, у) в пределе обращается во всю плоскость хОу, попада­ние в которую есть достоверное событие.