20.Сформулируйте основные свойства функции распределения и прв случайной величины.

Плотность распределения, плотность вероятности , плотность распределения вероятности в теории вероятностей — производная абсолютно непрерывной функции распределения.

Пусть — случайная величина с функцией распределения ; пусть существует неотрицательная функция такая, что для любых

тогда называется плотностью распределения случайной величины

Для любого борелевского множества

Любая неотрицательная интегрируемая функция удовлетворяющая условию номировки

является плотностью распределения некоторой случайной величины

Свойства плотности распределения

Из формулы P{Α ≤ X < Β}=F(Β)-F(Α)следует, что вероятность попадания случайной величины в заданный интервал определяется скоростью изменения функции распределения вероятностей на этом интервале. Скорость изменения непрерывной функции равна ее производной. Это позволяет ввести новую функцию для задания случайной величины.

Свойства плотности распределения f(x).

1. Всегда f(x)≥0, так как функция F(x) является неубывающей функцией.

2 Для функции распределения F(x) справедливо равенство: F(x)=_-∞∫^xf(t)dt.

3. Вероятность попадания случайной величины в заданный интервал [Α ; Β] равна: P{Α≤X<Β}=_Α∫^βf(t)dt.

4. Интеграл от плотности распределения вероятности по всей области задания случайной величины равен единице _-∞∫^∞f(t)dt=1 .

21Понятие равномерного закона распределения и его основные характеристики.

Випадкова величина має рівномірний закон розподілу, якщо її значення в межах деякого інтервалу 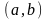однаково ймовірно розподілені (рис 2.1). Аналітичний запис рівномірної щільності розподілу ймовірності має вигляд

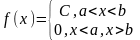де константа С визначається із рівності 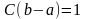, тому

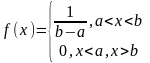
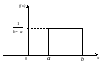
Рис. 2.1. Рівномірна щільність розподілу імовірності

Функція розподілу відповідає площі під кривою щільності розподілу лівіше точки X, тобто

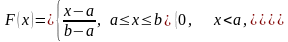
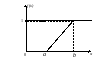Рис. 2.2. Функція розподілу рівномірно розподіленої величини

Визначимо числові характеристики випадкової величини з рівномірним розподілом.

Математичне очікування

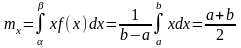Дисперсія

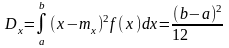
Середньоквадратичне відхилення

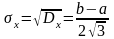Коефіцієнт асиметрії .

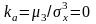Четвертий центральний момент

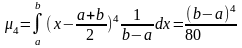Ексцес дорівнює

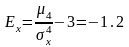
22.Понятие нормального закона распределения и его основные характеристики.

Нормальний закон розподілу найбільш часто зустрічається на практиці. Головна особливість, що виділяє його серед інших законів, полягає в тому, що він є граничним законом, до якого наближаються інші закони.

Нормальний закон розподілу (розподіл Гауса) характеризується щільністю розподілу ймовірності виду:

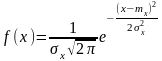
На рис 2.3 показано графік нормальної щільністю розподілу ймовірності.

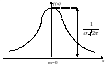
Рис. 2.3. Графік нормальної щільності розподілу ймовірності

Функція розподілу відповідає площі під кривою щільності розподілу лівіше точки X, тобто

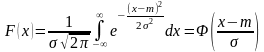, де 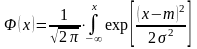- табулированный интеграл Лаплас

Графік функції F(х) наведений на рис 2.4.

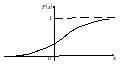
Рис. 2.4. Графік функції розподілу нормального закону

Математичне очікування 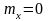Дисперсія 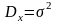Коефіцієнт асиметрії . Ексцес