41. Поясните свойства корреляционной функции.
Кореляційний аналіз - це сукупність методів виявлення кореляційної залежності, тобто коефіцієнта кореляції між двома випадковими величинами та процесами.
Кореляція – статистичний взаємозв'язок двох або декількох випадкових величин. При цьому, зміни однієї або декількох із цих величин приводять до систематичної зміни іншої або іншої величин. Математичною мірою кореляції двох випадкових величин служить кореляційний момент та коефіцієнт кореляції.
Кореляційний момент є характеристика системи випадкових величин, що описує, крім розсіювання двох випадкових величин X й Y, ще й зв'язок між ними.
а для безперервних - формулою
Для характеристики зв'язку між величинами (X, Y) у чистому вигляді переходять від моменту Кху до безрозмірної характеристики
(5.1)
де σх , σу — середні квадратичні відхилення величин X, У.
Ця характеристика називається коефіцієнтом кореляції величини Х и Y. Коефіцієнт кореляції обертається в нуль одночасно з кореляційним моментом; отже, для незалежних випадкових величин коефіцієнт кореляції дорівнює нулю.
42-43.Перечислите признаки стационарности случайного процесса узком смысле.
Автокорреляционная функция ССП является четной функцией,
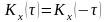
Это свойство вытекает из симметричности корреляционной функции.
2. Значение автокорреляционной функции при равно дисперсии ссп:
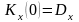
При
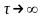значение автокорреляционной функции
стремится к нулю, т.е.
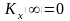
Значение автокорреляционной функции ССП при всегда больше или равно ее значенью при
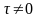
, т.е.
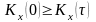
Какой случайный процесс называется эргодическим и при каких условиях?
Случа́йный проце́сс (случайная функция) в теории вероятностей — семейство случайных величин, индексированных некоторым параметром, чаще всего играющим роль времени или координаты.
Если при определении моментных функций стационарного случайного процесса операцию усреднения по статистическому ансамблю можно заменить усреднением по времени, то такой стационарный случайный процесс называется эргодическим.
45. Что такое гистограмма случайного процесса и как она строится?
Математическая статистика изучает случайные процессы на основе обработки статистических данных, которыми служат результаты наблюдений или измерений. Пусть наблюдается ССП . Как известно, для такого процесса одномерная плотность распределения вероятности не зависит от времени. Нахождение этой плотности сводится к построению гистограммы выполняется следующим образом
Г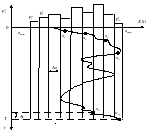
истограмма
случайного процесса
За время наблюдения Т получают N дискретных значений реализации случайного процесса, N — объем выборки. Чем меньше интервал дискретизации процесса и чем больше N. тем точнее выборка отображает вероятностные свойства рассматриваемого процесса.
46-47
А втокорреляционная функция ССП является четной функцией,
Э то свойство вытекает из симметричности корреляционной функции.
2. Значение автокорреляционной функции при равно дисперсии ссп:
З начение автокорреляционной функции ССП при всегда больше или равно ее значенью при
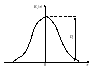
4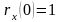
8.
Величина называется интервалом
корреляции и определяется либо долей
о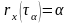
т
, либо половиной ширины основания
прямоугольника единичной высоты площадь
которого ровна площади под кривой
коэффициента корреляции
В первом случае для определения решают уравнение:
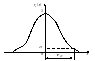
Во втором - для определения вычисляют интеграл
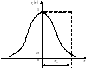
49.Стационарный случайный процесс (ССП) – это процесс, который протекает во времени приблизительно однородно, т.е. существенно не изменяются его вероятностные характеристики.Он имеет место в установившемся режиме работы системы при неизменных внешних условиях.
Для стационарного случайного процесса матожидание и дисперсия являются константами, т.е.
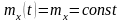
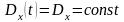
Условие для матожидания не является существенным, так как от исходного процесса всегда можно перейти к центрированному процессу, для которого матожидание тождественно равно нулю и является постоянной величиной, т.е. процесс, нестационарный только за счет переменного матожидания, всегда может быть приведен к стационарному.