Вариант 25
1-тапсырма. Екi ықтималдық операциялар берiлген, мұнда Х – бiрiншi қаржылық операцияның кездейсоқ табысы, У – екiншi операцияның кездейсоқ табысы. Әр операциядан күтiлетiн орта табысты, операция дисперсиясын D(Х) және әр операцияның тәуекелдiк бағасын тап. Қай операцияның тәуекелдiгi аз. Әр операция үшiн үлестiрiм функциясын F(x) құр.
xi |
50 |
60 |
70 |
90 |
|
yi |
8 |
12 |
15 |
20 |
p i |
0,7 |
0,1 |
0,1 |
0,1 |
|
pi |
0,1 |
0,6 |
0,1 |
0,2 |
Задание 2. Вероятность того, что в библиотеке необходимая студенту книга свободна, равна 0,3.Составить закон распределения числа библиотек, которые посетит студент, если в городе 4 библиотеки.
Задание 3. Дана интегральная функция распределения непрерывной случайной величины Х. Найти математическое ожидание, дисперсию и среднее квадратическое отклонение этой величины. Построить графики интегральной и дифференциальной функций.
Задание 4. Предполагается, что случайные отклонения текущей цены акции подчиняются нормальному закону распределения со средним квадратическим отклонением 3 (ден. ед.) и математическим ожиданием 10(ден.ед.). Найти:
1).выражение плотности вероятности
3).вероятность того, что случайная величина Х примет значение принадлежащее интервалу (5;17);
4).вероятность того, что значение Х будет отклоняться от 10 не более чем на величину 5.
Задание 5. Случайная величина задана плотностью распределения:
f (x)=
Определить: 1) параметр k;
2) функцию распределения F(x);
Вариант 26
1-тапсырма. Екi ықтималдық операциялар берiлген, мұнда Х – бiрiншi қаржылық операцияның кездейсоқ табысы, У – екiншi операцияның кездейсоқ табысы. Әр операциядан күтiлетiн орта табысты, операция дисперсиясын D(Х) және әр операцияның тәуекелдiк бағасын тап. Қай операцияның тәуекелдiгi аз. Әр операция үшiн үлестiрiм функциясын F(x) құр.
xi |
-1 |
3 |
5 |
8 |
|
|
yi |
1 |
3 |
5 |
9 |
pi |
0,3 |
0,4 |
0,1 |
0,2 |
|
|
pi |
0,4 |
0,1 |
0,2 |
0,3 |
Задание 2. В магазин поступила обувь с двух фабрик в соотношении 2:3. Куплено 4 пары обуви. Найти закон распределения числа купленных пар обуви, изготовленной первой фабрикой.
Задание 3. Дана интегральная функция распределения непрерывной случайной величины Х. Найти математическое ожидание, дисперсию и среднее квадратическое отклонение этой величины. Построить графики интегральной и дифференциальной функций.
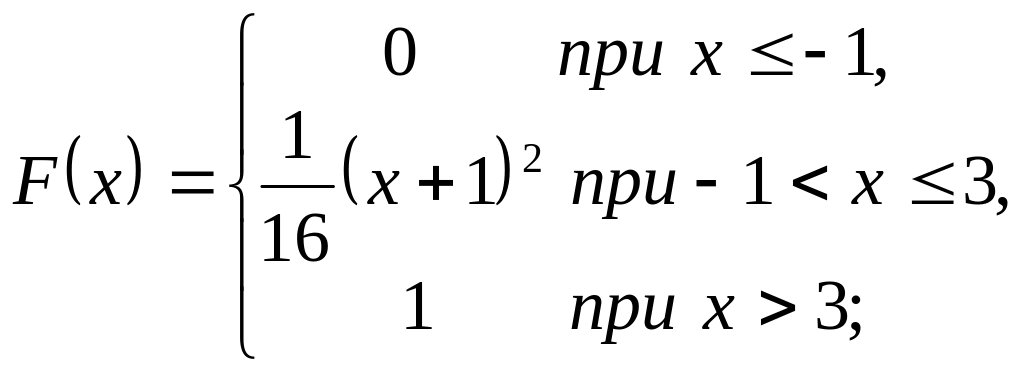
Задание 4. Предполагается, что случайные отклонения текущей цены акции подчиняются нормальному закону распределения со средним квадратическим отклонением 9 (ден. ед.) и математическим ожиданием 40 (ден.ед.). Найти:
1).выражение плотности вероятности
3).вероятность того, что случайная величина Х примет значение принадлежащее интервалу (40;48);
4).вероятность того, что значение Х будет отклоняться от 40 не более чем на величину 4.
Задание 5. Случайная величина задана плотностью распределения:
f (x)=
Определить: 1) параметр k;
2) функцию распределения F(x);