1.Виды и свойства ошибок геодезических измерений

Определением величины ошибок и их свойств занимается специальная дисциплина «Теория ошибок геодезических измерений».В практике различают 3 вида ошибок:а)грубые – пол-ся в рез-те грубых просчетов и неисправности приборов (просчет количества лент в длине линии, ошибка в отсчете десятков градусов на лимбе или числа дециметров на рейке). Они могут быть обнаружены и исключены путем повторного измерения величины.б)систематические – проявляются регулярно, обязательно в каждом измерении и обязательно одинаковы по модулю и знаку, действуют по одному принципу. Они вызваны в основном плохой юстировкой или неисправностью инструментов и приборов (20-ти метровая лента короче на 1см, коллимационная ошибка в теодолите). Исключаются из результатов измерений введением поправок и специальной методикой измерений (углы β при КП и КЛ, при нивелировании плечи делают равными, в длины линий вводят поправки за компарирование).в)случайные – являются следствием несовершенства органов чувств человека и недостаточной точности применяемых инструментов и приборов. Они не могут быть исключены из результатов измерений, но их влияние может быть ослаблено на основе изучения их свойств.

Если Х – истинное значение измеряемой величины, ℓ - измеренное значение, то случайная ошибка ∆ выражается формулой ∆=ℓ-Х.

Если одна и та же величина измерена несколько раз, то и количество ошибок будет большим. Получается ряд ошибок. Если измерения производятся приборами одинаковой точности, наблюдателями одинаковой квалификации, в одинаковых окружающих условиях, то они называются равноточными. Иначе-неравноточными.

В основу изучения случайных ошибок положено 4 их свойства, выведенных из изучения рядов ошибок равноточных измерений.1) При данных условиях измерений случайные ошибки не могут превосходить по абсолютной величине известного предела (свойство ограниченности).2) Одинаковые по абсолютной величине положительные и отрицательные случайные ошибки равно возможны, одинаково часто встречаются в ряду измерений.3) Чем больше абсолютная величина случайной ошибки, тем реже такая ошибка встречается в ряду измерений.4) Среднее арифметическое из случайных ошибок равноточных измерений одной и той же величины имеет тенденцию стремиться к 0 при неограниченном возрастании числа измерений (свойство компенсации). Математически это записывается так

Если соблюдены все четыре свойства в ряде ошибок, то говорят о «нормальном распределении».5) Если∆₁ ∆_n - 1-й ряд измерений; ∆₁' ∆_n' – 2-ой ряд измерений,

т о 4-ое свойство распространяется и на сумму попарных произведений, то есть n→ ∞

2. Средняя квадратическая ошибка алгебраической суммы измеренных величин Функция вида z=x+y (суммы ); m_z=?

Дано: х – измерено несколько раз с ошибками ∆х₁; ∆х₂,… ∆х_{n; ;} у – измерено несколько раз с ошибками ∆у₁, ∆у₂,… ∆у_{n ;}z – будет вычислено несколько раз с ошибками ∆z₁, ∆z₂,… ∆z_n. ; Эта же формула справедлива для функции вида z=x-y, так как после выше приведенных рассуждений перед последним членом будет знак (-). Но он все равно стремится к нулю.Поэтому можно сделать вывод, что квадрат средней квадратической ошибки алгебраической суммы двух аргументов равен сумме квадратов средних квадратических ошибок слагаемых.Если m_х=m_у=m, то m_z=± .Пусть 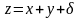, перепишем . Тогда можно записать: , но , поэтому 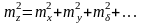.Если , то при n слагаемых , то есть квадрат средней квадратической ошибки суммы аргументов равен сумме квадратов средних квадратических ошибок слагаемых.Средняя квадратическая ошибка алгебраической суммы измеренных с одинаковой точностью величин в раз больше средней квадратической ошибки одного слагаемого.