1.5. Классификация задач исследования операций по уровню информации о ситуации

Детерминированый уровень - наиболее простой уровень информации о ситуации - когда условия, в которых принимаются решения, известны полностью.

Стохастический уровень - уровень, при котором известно множество возможных вариантов условий и их вероятностное распределение.

Неопределенный уровень - уровень, когда известно множество возможных вариантов, но без какой либо информации об их вероятностях.

2. Обзор основных разделов

2.1. Обзор основных направлений линейного и математического программирования

Математическое программирование  очень обширная область современной математики и её обстоятельное изложение потребовало бы несколько томов книг. Поэтому укажем лишь основные направления, по которым велись и ведутся математические исследования.

2.1.1. Развитие симплекс-метода

В данном пособии изложен лишь простейший алгоритм симплекс-метода. В настоящее время существует много модификаций этого метода, позволяющих существенно сократить время счета, сделать алгоритм нечувствительным к вырожденности опорных планов, повысить размерность решаемых задач, решать так называемые блочные задачи и т.д. Несмотря на обилие этих модификаций, продолжают появляться все новые и новые его варианты.

2.1.2. Целочисленное линейное программирование

В целом ряде решаемых задач линейного программирования на переменные накладывается дополнительное условие их целочисленности. Действительно, ведь нельзя изготовить, скажем, 1/2 стола или сшить 1/3 костюма. Когда наложено дополнительное условие целочисленности переменных , соответствующая задача носит название задачи целочисленного линейного программирования.

Простое округление до целых чисел здесь не помогает  план может получиться не оптимальным. Поэтому приходится разрабатывать специальные алгоритмы решения таких задач, к наиболее известным из которых относятся так называемые алгоритмы Гомори, основанные на так называемой идее отсечения. Более подробно о целочисленном программировании можно узнать здесь.

2.1.3. Булевское программирование

К частному случаю задачи целочисленного линейного программирования относятся задачи, где переменные могут принимать всего лишь два значения  0 и 1. Соответствующие задачи часто называют задачами булевского программирования. Наиболее известные из этих задач  это задача о назначениях (какого работника на какую работу поставить), задача выбора маршрута (задача коммивояжера, задача почтальона), задача о максимальном паросочетании и т.д.

Для решения задач этого типа разрабатываются очень специфические алгоритмы, основанные на комбинаторике, графах и т.д.

2.1.4. Стохастическое линейное программирование

Бывает много практических ситуаций, когда коэффициенты целевой функции, коэффициенты в матрице коэффициентов, коэффициенты ограничений - являются случайными величинами. В этом случае сама целевая функция становится случайной величиной, и ограничения типа неравенств могут выполняться лишь с некоторой вероятностью. Приходится менять постановку самих задач с учётом этих эффектов и разрабатывать совершенно новые методы их решения. Соответствующий раздел получил название стохастического программирования.

2.1.5. Квадратичное программирование

Под квадратичным программированием понимаются задачи следующего вида (в матричных обозначениях)

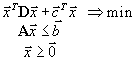
где симметричная матрица размерности . Задачи линейного программирования являются частным случаем этих задач  они получаются при =0. Способы решения этих задач во многом определяются видом матрицы : если  положительно определённая матрица, то целевая функция будет выпуклой и любой её локальный минимум будет глобальным. Если  отрицательно определённая матрица, то может быть несколько локальных минимумов, но глобальный минимум, если он существует, достигается обязательно на вершине допустимой области. В общем случае, когда собственные числа матрицы имеют разные знаки, задача очень сильно усложняется, так как глобальный минимум может достигаться где угодно  и внутри области и на её границе.