

Алек Власов. ЛЕКЦИИ ПО ФИЗИКЕ |
1 |
|
Оптика. Квантовые свойства излучения. Лекция № 13
Лекция № 13
Тема лекции:
Формула Планка и квантование энергии излучения
Рассматриваемые вопросы:
1.Стоячие волны в полости - модели чёрного тела……………………………1
2.Формула Рэлея-Джинса…………………………………………………..……7
3.Формула Планка………………………………………………………….…...10
4.Тормозное рентгеновское излучение………………………….………….…15
1.СТОЯЧИЕ ВОЛНЫ В ПОЛОСТИ – МОДЕЛИ ЧЁРНОГО ТЕЛА
При нахождении функции r 0 |
(ν ,T ) возникает |
ν |
|
необходимость в подсчете числа стоячих волн, которые могут возбуждаться в объёме конечных размеров, в частности в полости с малым отверстием, принимаемой в качестве модели чёрного тела.
Рассмотрим вначале одномерный случай (рис. 1).
Рис. 1.
Пусть вдоль оси х бегут во встречных направлениях две плоские волны, возникающие в результате отражения от стенок, расположенных в точках х = О и х = а
Алек Власов. ЛЕКЦИИ ПО ФИЗИКЕ |
2 |
|
|
Оптика. Квантовые свойства излучения. Лекция № 13 |
|
Уравнения волн имеют вид |
|
|
(1) |
(за счет выбора начала отсчета времени начальная фаза первой волны сделана равной нулю).
Мы знаем, что в этом случае в области 0 ≤ x ≤ a возникает стоячая волна, причем в зависимости от реальных условий на границах области бывают либо узлы, либо пучности. Так, например, на концах струны наблюдаются узлы, а на концах закрепленного в середине стержня — пучности.
Из уравнений (1) видно, что для того, чтобы на границе х = 0 возникала пучность, фаза α должна быть равна нулю (тогда в точках с х = 0 колебания будут происходить в одинаковой фазе).
В этом случае при отражении от границы фаза волны не изменяется. Это следует из того, что в непосредственной близости к стенке (при х ≈ 0) фазы колебаний ξ1 и ξ2 совпадают. Для того же, чтобы на границе x = 0 возникал узел, фаза α должна быть равна π (тогда в точках с x = 0 колебания ξ1 и ξ2 будут происходить в противофазе). В этом случае при отражении от границы фаза волны претерпевает скачок на π .
Итак, в случае, когда на границах области наблюдаются пучности, уравнения (1) имеют вид

Алек Власов. ЛЕКЦИИ ПО ФИЗИКЕ |
3 |
|
Оптика. Квантовые свойства излучения. Лекция № 13
В случае, когда на границах области наблюдаются узлы, уравнения (1) выглядят следующим образом:
Сложение колебаний ξ1 и ξ2 в случае пучностей на границах приводит к уравнению
(2)
и в случае узлов на границах — к уравнению
(3)
Для того чтобы и на другой границе (т. е. при х = а) наблюдалась пучность (в случае, описываемом уравнением (2)) либо узел (в случае, описываемом уравнением (3)), необходимо, чтобы произведение ka было целым кратным π :
ka = nπ .
Таким образом, независимо от того, что наблюдается на границах области (пучности или узлы), модуль волнового вектора должен иметь значения
|
|
|
|
(4) |
Отсюда следует |
|
|
|
|
|
n = |
a |
k |
(5) |
|
|
|||
|
|
π |
|
|
Из (5) следует, что |
в интервале значений волнового вектора |
k |
||
число стоячих волн |
Nk равно |
|
||
Алек Власов. ЛЕКЦИИ ПО ФИЗИКЕ |
4 |
|||
|
||||
Оптика. Квантовые свойства излучения. Лекция № 13 |
|
|||
Значения |
Nk |
образуют |
дискретную |
|
последовательность. Заменив эту последовательность непрерывной функцией, можно написать
(6)
Модуль волнового вектора связан с частотой ω и скоростью v соотношением
(7)
Соответственно
(8)
(мы считаем, что дисперсии нет, т. е. v = const).
Заменив в (6) dk через dω v , придём к формуле
v , придём к формуле
(9)
где dNω — число стоячих волн, частоты которых лежат в интервале от ( ω до ω + dω ).
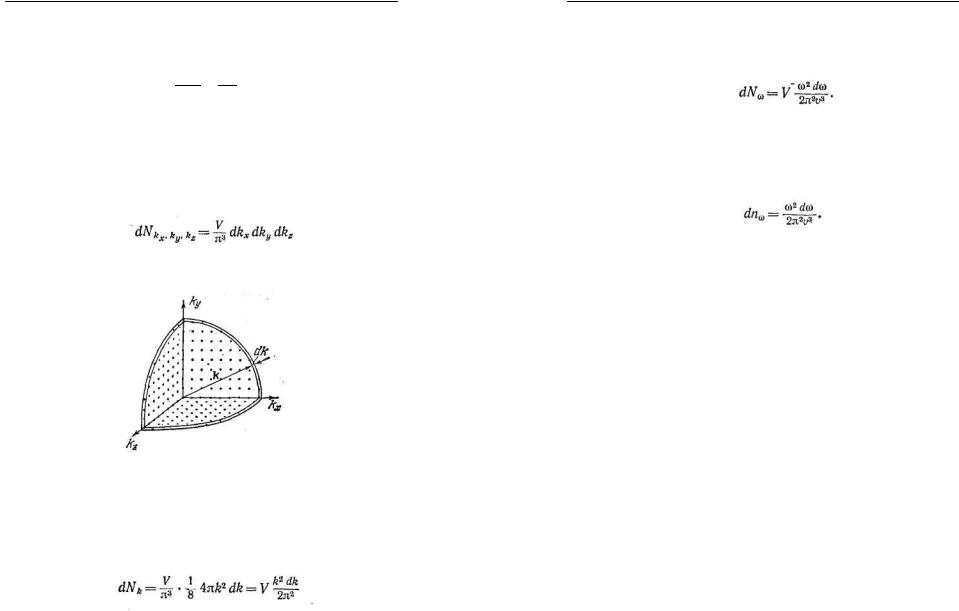
Теперь рассмотрим трёхмерный случай, рис. 2.
Рис. 2.
Алек Власов. ЛЕКЦИИ ПО ФИЗИКЕ |
5 |
|
Оптика. Квантовые свойства излучения. Лекция № 13
По аналогии с формулой (4) на долю каждой точки приходится объем
π 3 = π 3 abc V
(V — объем области).
Число стоячих волн, у которых проекции волновых векторов заключены в пределах от kx до kx + dkx, от ky до ky + dky и от kz до k + dkz, определяется по аналогии с (6) выражением
(10)
В k -пространстве с осями kx, ky, kz каждой стоячей волне отвечает точка в первом октанте (рис. 3).
Рис. 3.
Число стоячих волн, у которых модуль волнового вектора лежит в пределах от k до k + dk, равно количеству точек, попадающих в пределы 1/8 шарового слоя радиуса k и толщины dk (см. рис. 3). Следовательно
(11)
Алек Власов. ЛЕКЦИИ ПО ФИЗИКЕ |
6 |
|
|
Оптика. Квантовые свойства излучения. Лекция № 13 |
|
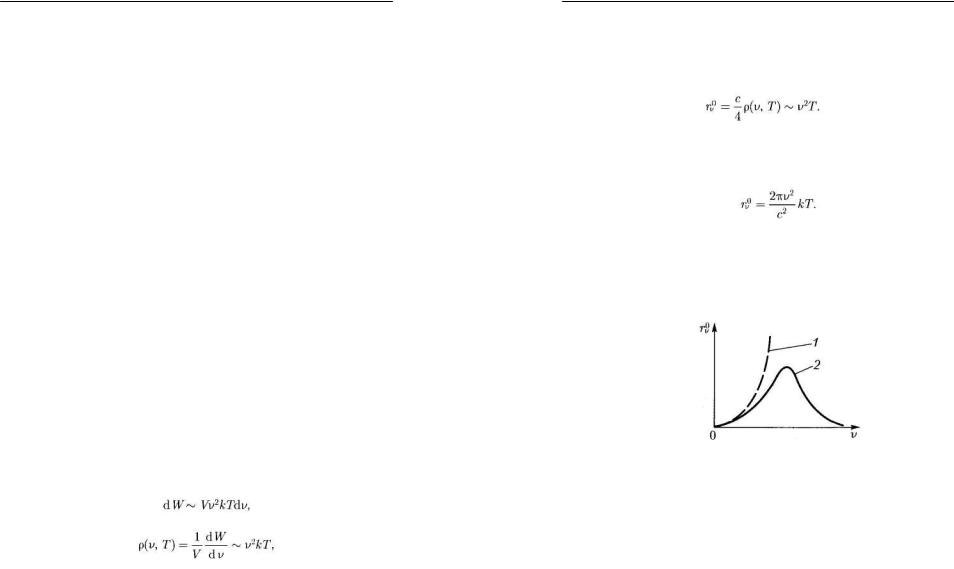
Приняв во внимание формулы (7) и (8), получим число стоячих волн, частоты которых попадают в интервал от ω до ω + dω :
(12)
Выражение (12) пропорционально объему полости V. Поэтому можно говорить о числе стоячих волн dnω ,
приходящихся на единицу объёма полости. Это число равно (для одной поляризации света):
(13)
Таким образом, формула (13) задаёт число осцилляторов dnω чёрного тела единичного объёма, излучающих в полосе частот dω на произвольной частоте ω .
Алек Власов. ЛЕКЦИИ ПО ФИЗИКЕ |
7 |
|
Оптика. Квантовые свойства излучения. Лекция № 13
2. ФОРМУЛА РЭЛЕЯ-ДЖИНСА
Рэлей подошел (1900) к изучению спектральных закономерностей черного излучения с позиций статистической физики, а не термодинамики, как это делали его предшественники. Он рассмотрел равновесное (черное) излучение в замкнутой полости с зеркальными стенками как совокупность пространственных стоячих электромагнитных волн. Частоты этих волн должны удовлетворять определенным условиям, подобным условиям для частот стоячих упругих волн в стержнях. Рэлей показал, что число dnтаких собственных частот, находящихся в интервале от v до v + dv, пропорционально объему полости V, квадрату частоты v и ширине интервала dv:
dn ~ Vv2dv.
Колебания с разными собственными частотами совершаются независимо друг от друга. Каждой собственной частоте соответствует своя колебательная степень свободы черного излучения. Применив закон классической статистической физики о равном распределении энергии по всем степеням свободы равновесной системы, Рэлей показал, что энергия d W излучения в полости, соответствующая интервалу частот от v до v + dv,
Алек Власов. ЛЕКЦИИ ПО ФИЗИКЕ |
8 |
|
|
Оптика. Квантовые свойства излучения. Лекция № 13 |
|
где кТ — средняя энергия, приходящаяся на одну колебательную степень свободы. Таким образом, Рэлей получил, что
В дальнейшем Рэлей и Джинс уточнили эту формулу, вычислив значение коэффициента пропорциональности:
(14)
Формула Рэлея —Джинса (14) хорошо согласовалась с данными опытов только в области малых частот излучения (кривая 1; рис. 4).
Рис. 4.
Для больших частот она была явно неверна (кривая 2). Формула Рэлея —Джинса противоречила также закону смещения Вина и закону Стефана —Больцмана: по
формуле (14) r 0 монотонно возрастает с ростом частоты,
ν
не имея максимума, а Rэ0 при любой температуре обращается в бесконечность:

Алек Власов. ЛЕКЦИИ ПО ФИЗИКЕ |
9 |
|
Оптика. Квантовые свойства излучения. Лекция № 13
(15)
Работы Рэлея и Джинса показали, что последовательное применение классической физики к исследованию спектрального состава черного излучения дает абсурдные результаты, находящиеся в противоречии с законом сохранения энергии.
Невозможность отыскания методами классической теоретической физики такого выражения для функции Кирхгофа, которое согласовывалось бы с данными эксперимен тов во всем интервале частот от 0 до ∞ , получило образное название «ультрафиолетовой
катастрофы». (Смысл названия заключается в том, что нарушение закона сохранения энергии происходит при подстановке в интеграл (15) бесконечности в качестве верхнего «ультрафиолетового» предела частот).
Алек Власов. ЛЕКЦИИ ПО ФИЗИКЕ |
10 |
|
Оптика. Квантовые свойства излучения. Лекция № 13
3. ФОРМУЛА ПЛАНКА
Найти правильное выражение для функции Кирхгофа и дать теоретическое обоснование спектральным закономерностям черного излучения впервые удалось немецкому физику М. Планку.
Выше уже отмечалось, что объемная плотность энергии равновесного излучения в замкнутой полости и распределение энергии этого излучения по частотам зависят только от температуры стенок полости. Материал стенок, т.е. конкретные свойства системы, с которой связано равновесное излучение, не играет никакой роли.
В своих расчетах Планк выбрал наиболее простую модель излучающей системы (стенок полости) в виде совокупности линейных гармонических осцилляторов (электрических диполей) со всевозможными собственными частотами ν (см. предыдущий раздел о стоячих волнах).
Исходя из того, что в состоянии термодинамического равновесия расход энергии на излучение осцилляторов с собственной частотой v должен полностью компенсироваться в результате поглощения этими осцилляторами энергии падающего на них излучения, Планк показал (1899), что
(16)

Алек Власов. ЛЕКЦИИ ПО ФИЗИКЕ |
11 |
|
Оптика. Квантовые свойства излучения. Лекция № 13
где (wv) — средняя энергия осциллятора с собственной частотой v.
Если бы для ее определения Планк, подобно Рэлею, воспользовался законом классической статистической физики о равном распределении энергии по всем степеням свободы равновесной системы, то он получил бы, что (wv) = kT. При этом его формула (15) совпала бы с формулой Релея-Джинса (14).
Однако Планк пытался найти выражение для (wv), исходя из термодинамических соотношений. Он был убежден, что между энтропией S осциллятора и его средней энергией должна существовать сравнительно простая связь.
В октябре 1900 г. Планку удалось подобрать такой вид зависимости  wν
wν  , при котором
, при котором
(17)
где а1 и а2 — постоянные коэффициенты.
Оказалось, что формула (17) хорошо согласуется с результатами экспериментов при всех частотах и температурах. Поэтому следующий основной этап исследования, завершенный Планком в декабре 1900 г., состоял в выяснении физического смысла и теоретическом обосновании столь удачно угаданного им соотношения между энтропией и средней энергией осциллятора.
Применив статистический метод Больцмана, Планк вывел искомое соотношение. Однако для этого ему
Алек Власов. ЛЕКЦИИ ПО ФИЗИКЕ |
12 |
|
|
Оптика. Квантовые свойства излучения. Лекция № 13 |
|
пришлось ввести квантовую гипотезу, согласно которой энергия атомов-осцилляторов может изменяться дискретно, порциями, пропорциональными некоторой элементарной порции — кванту энергии wν 0 : wν = nwν 0 , где
n = 0, 1,2,....
Если считать, что распределение осцилляторов по возможным дискретным энергетическим состояниям описывается законом Больцмана, то вероятность нахождения осцилляторов в состоянии с энергией wν 0 при
термодинамической температуре T равна
Здесь с — постоянный коэффициент, определяемый из условия нормировки
или
Средняя энергия осциллятора
откуда
Алек Власов. ЛЕКЦИИ ПО ФИЗИКЕ |
13 |
|
Оптика. Квантовые свойства излучения. Лекция № 13
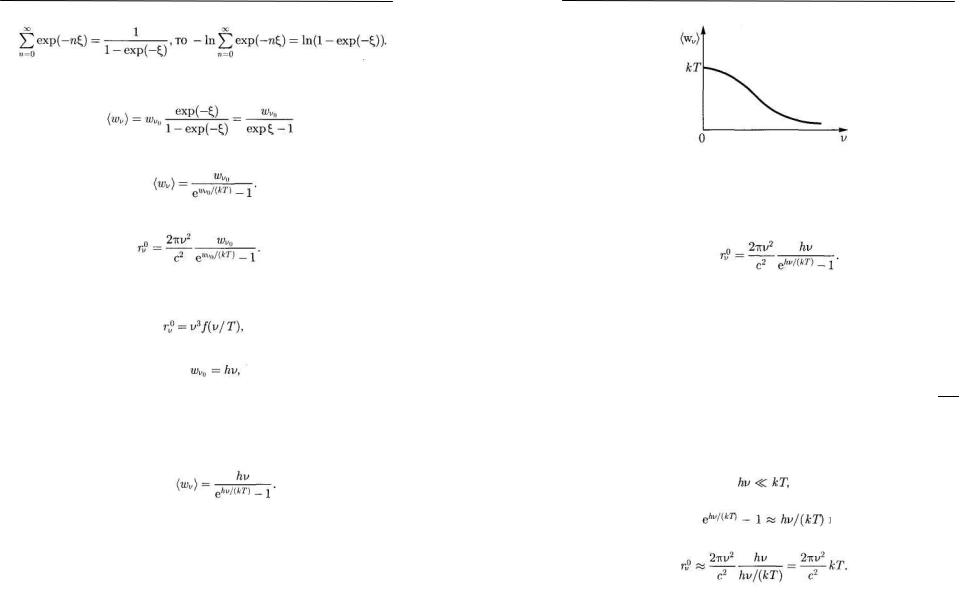
Таким образом,
или
(18)
Поэтому, согласно (16),
(19)
Из сопоставления (18) с формулой Вина (см. предыдущую лекцию)
следует, что квант энергии пропорционален частоте ν :
(20)
где h — универсальная постоянная, получившая название
постоянной Планка.
Таким образом, средняя энергия осциллятора
(21)
Эта зависимость (wv) от v показана на рис. 5.
Алек Власов. ЛЕКЦИИ ПО ФИЗИКЕ |
14 |
|
Оптика. Квантовые свойства излучения. Лекция № 13
Рис. 5.
Окончательное выражение формулы Планка:
(22)
Здесь h = 6,626176 10−34 Дж . с – постоянная Планка. Размерность «энергия × время» соответствует величине, называемой «действием». Поэтому постоянную Планка называют также квантом действия.
Используется также постоянная Планка в виде h = h = 2π
=1,054 Дж . с.
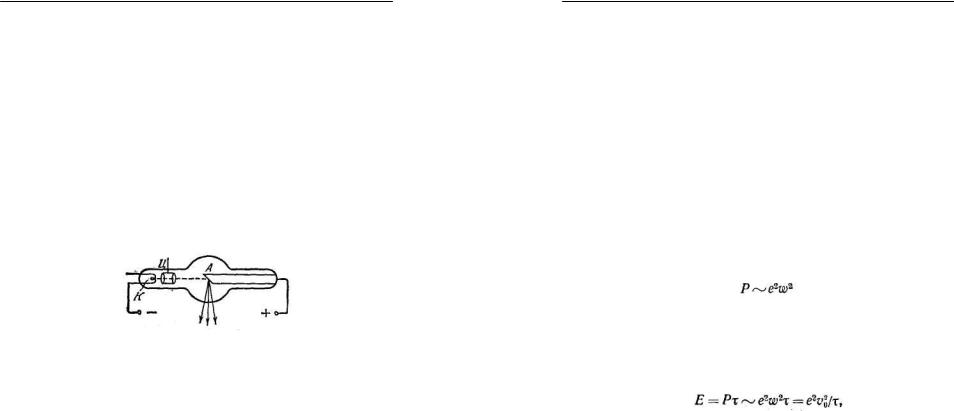
Следует отметить, что в области малых частот, когда
имеет место
и формула Планка (22) переходит в формулуРелея-Джинса (14):
Алек Власов. ЛЕКЦИИ ПО ФИЗИКЕ |
15 |
|
Оптика. Квантовые свойства излучения. Лекция № 13
4.ТОРМОЗНОЕ РЕНТГЕНОВСКОЕ ИЗЛУЧЕНИЕ
Впредыдущем разделе этой лекции мы узнали, что для объяснения свойств теплового излучения пришлось ввести представление об испускании электромагнитного излучения порциями энергии ε , равными ε = hλ = hω .
Квантовая природа излучения подтверждается также существованием коротковолновой границы тормозного рентгеновского спектра.
Рентгеновские лучи возникают при бомбардировке быстрым электронами твердых мишеней, рис. 6.
Рис. 6.
Рентгеновская трубка (рис. 6) представляет собой эвакуированный баллон с несколькими электродами Нагреваемый током катод К служие источником свободных электронов, испускаемых вследствие термоэлектронной эмиссии. Цилиндрический электрод Ц предназначен для фокусировки электронного пучка. Мишенью является анод А, который называют также антикатодом. Его делают из тяжелых металлов (W, Сu, Pt и т. д.).
Ускорение электронов осуществляется высоким напряжением, создаваемьго между катодом и антикатодом. Почти вся энергия электронов вы деляется на антикатоде в виде тепла (в излучение превращаете лишь 1—3 %
Алек Власов. ЛЕКЦИИ ПО ФИЗИКЕ |
16 |
|
Оптика. Квантовые свойства излучения. Лекция № 13
энергии). Поэтому в мощных трубках антикатод приходится интенсивно охлаждать. С этой целью в теле антикатода делаются каналы, по которым циркулирует охлаждающая жидкость (вода или масло).
Если между катодом и антикатодом приложено напряжение U, электроны разгоняются до энергии eU. Попав в вещество антикатода, электроны испытывают сильное торможение и становятся источником электромагнитных волн.
Мощность излучения Р пропорциональна квадрату заряда электрона и квадрату его ускорения:
Предположим в первом приближении, что ускорение электрона w постоянно в течение всего времени торможения τ . Тогда мощность излучения также будет постоянной, и за время торможения электрон излучит энергию
где v0 — начальная скорость электрона.
Полученный результат показывает, что заметное излучение может наблюдаться лишь при резком торможении быстрых электронов. На рентгеновские трубки подается напряжение до 50 кВ. Пройдя такую разность потенциалов, электрон приобретает скорость, равную 0,4 с.
Алек Власов. ЛЕКЦИИ ПО ФИЗИКЕ |
17 |
|
Оптика. Квантовые свойства излучения. Лекция № 13
Направив ускоренный пучок электронов на твердую мишень, получают рентгеновские лучи малой длины волны. Чем меньше длина волны, тем меньше поглощаются лучи в веществе. Поэтому рентгеновские лучи обладают большой проникающей способностью.
При |
достаточно большой скорости электронов, |
кроме |
тормозного и з л у ч е н и я (т. е. излучения, |
обусловленного торможением электронов), возбуждается
также |
х а р а к т е р и с т и ч е с к о е |
и з л у ч е н и е |
||
(вызванное |
возбуждением |
внутренних |
электронных |
|
оболочек атомов антикатода). |
|
|
||
Здесь нас будет интересовать лишь тормозное излучение.
Согласно классической электродинамике при торможении электрона должны возникать волны всех длин—от нуля до бесконечности.
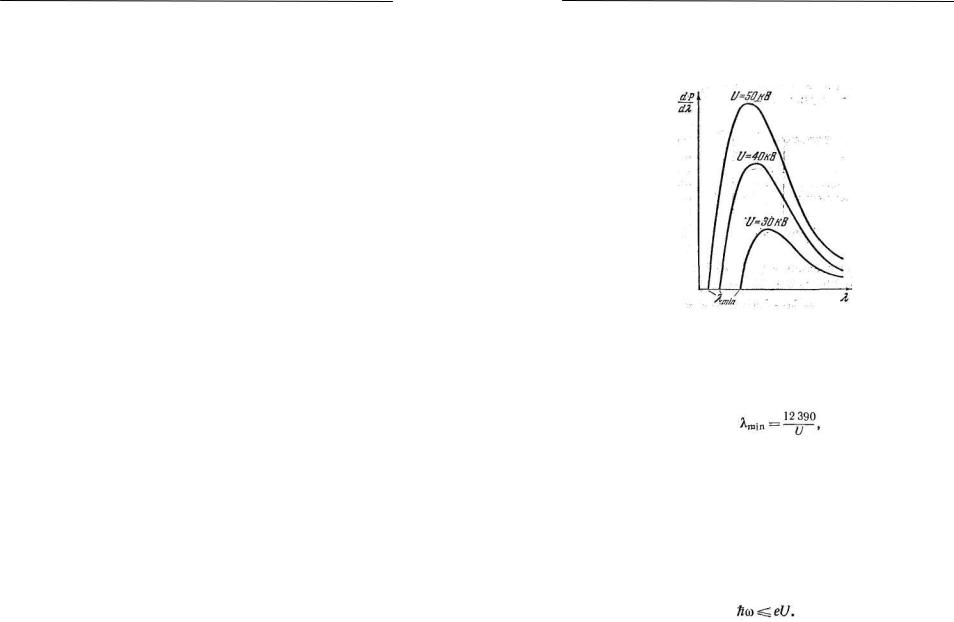
Длина волны, на которую приходится максимум мощности излучения, должна уменьшаться по мере увеличения скорости электронов, т. е. напряжения на трубке U. На рис. 6 даны экспериментальные кривые распределения мощности тормозного рентгеновского излучения по длинам волн, полученные для разных значений U. Как видно из рисунка, выводы теории в основном подтверждаются на опыте.
Однако имеется одно принципиальное отступление от требований классической электродинамики. Оно заключается в том, что кривые распределения мощности не
Алек Власов. ЛЕКЦИИ ПО ФИЗИКЕ |
18 |
|
Оптика. Квантовые свойства излучения. Лекция № 13
идут к началу координат, а обрываются при конечных значениях длины волны λmin .
Рис. 7.
Экспериментально установлено, что коротковолновая граница тормозного рентгеновского спектра λmin связана с ускоряющим напряжением U соотношением
(23)
где λmin выражена в ангстремах, U — в вольтах.
Существование коротковолновой границы непосредственно вытекает из квантовой природы излучения. Действительно, если излучение возникает за счет энергии, теряемой электроном при торможении, то величина кванта hω не может превысить энергию электрона eU
Алек Власов. ЛЕКЦИИ ПО ФИЗИКЕ |
19 |
|
Оптика. Квантовые свойства излучения. Лекция № 13
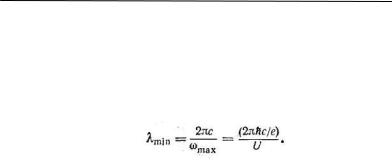
Отсюда получается, что частота излучения не может превысить значения
ωmax = eU  h ,
h ,
а следовательно, длина волны не можп быть меньше значения
(24)
Таким образом, мы пришли к эмпирическому соотношению (23).
Найденное из сопоставления формул (23) и (24) значение h хорошо согласуется со значениями, определенными иными способами.
Из всех методов определения h метод, основанный на измерении коротковолновой границы тормозного рентгеновского спектра, считается самым точным.
---------
