

Алек Власов. ЛЕКЦИИ ПО ФИЗИКЕ |
1 |
|
Оптика. Квантовые свойства излучения. Лекция № 2
Лекция № 2
Тема лекции:
Основы геометрической оптики
Рассматриваемые вопросы:
1.Законы геометрической оптики……………………...…………………………1
2.Принцип Ферма………………………………………….. ……………………..3
3.Таутохронные лучи……………………………………………...………………7
4.Преломление одной сферической поверхности…...…………………………..9
5.Тонкая линза…………………………………………………………………....14
6.Сферическое зеркало…………………..……………………………………….19
1.ЗАКОНЫ ГЕОМЕТРИЧЕСКОЙ ОПТИКИ
Длины воспринимаемых глазом световых волн очень малы (порядка 10-7 м). Поэтому, как упоминалось в предыдущей лекции, распространение видимого света можно в первом приближении рассматривать, отвлекаясь от его волновой природы и полагая, что свет распространяется вдоль некоторых линий, называемых лучами. В предельном случае, соответствующем λ → 0 , законы оптики можно сформулировать на языке геометрии. В соответствии с этим раздел оптики, в котором пренебрегают конечностью длин волн, называется геометрической оптикой. Другое название этого раздела — лучевая оптика.
Основу геометрической оптики образуют четыре закона:
1)закон прямолинейного распространения света;
2)закон независимости световых лучей;
3)закон отражения света;
4)закон преломления света.
Алек Власов. ЛЕКЦИИ ПО ФИЗИКЕ |
2 |
|
|
||
Оптика. Квантовые свойства излучения. Лекция № 2 |
|
|
Закон |
прямолинейного распространения |
|
утверждает, |
что в однородной среде свет |
|
распространяется прямолинейно.
Этот закон является приближенным: при прохождении света через очень малые отверстия наблюдаются отклонения от прямолинейности, тем большие, чем меньше отверстие.
Закон независимости световых лучей утверждает,
что лучи при пересечении не возмущают друг друга.
Пересечения лучей не мешают каждому из них распространяться независимо друг от друга. Этот закон справедлив лишь при не слишком больших интенсивностях света. При интенсивностях, достигаемых с помощью лазеров, независимость световых лучей перестает соблюдаться.
Закон отражения – отраженный луч лежит в плоскости падения, причём угол отражения равен углу падения (i′ = i ).
Закон преломления (Закон Снеллиуса) – преломлённый луч лежит в плоскости падения, а угол
преломления связан суглом падения соотношением: |
|
||||
|
sin i |
= |
nr |
= n , |
(1) |
|
|
|
|||
|
sin r ni |
ri |
|
||
|
|
|
|||
где i – угол падения, r – угол преломления (рефракции), nr – показатель преломления в среде распространения преломлённого луча, nr – показатель преломления в среде распространения падающего луча; nri – относительный показатель преломления сред.

Алек Власов. ЛЕКЦИИ ПО ФИЗИКЕ |
3 |
|
Оптика. Квантовые свойства излучения. Лекция № 2
2. ПРИНЦИП ФЕРМА
Воснову геометрической оптики может быть положен принцип, установленный французским математиком Ферма в середине XVII столетия. Из этого принципа вытекают законы прямолинейного распространения, отражения и преломления света.
Вформулировке самого Ферма принцип гласит, что
свет распространяется по такому пути, для прохож- дения которого ему требуется минимальное время.
Рис. 1.
Для прохождения участка пути ds (рис. 1) свету требуется время dt = ds/v, где v — скорость света в данной точке среды. Заменив v через c n , где с –
n , где с –
скорость света, n – показатель преломления, получим, что
dt = 1 nds . c
Следовательно, время τ , затрачиваемое светом на прохождение пути от точки 1 до точки 2, равно
|
1 |
2 |
|
|
τ = |
∫n ds . |
(2) |
||
c |
||||
|
1 |
|
||
|
|
|
Имеющая размерность длины величина
Алек Власов. ЛЕКЦИИ ПО ФИЗИКЕ |
4 |
|
|
Оптика. Квантовые свойства излучения. Лекция № 2 |
|
2 |
|
L = ∫n ds . |
(3) |
1 |
|
называется оптической длиной пути. |
|
В однородной среде оптическая длина пути равна произведению геометрической длины пути s на показатель преломления среды n :
L = ns . |
(4) |
Согласно (2) и (3): |
|
τ = L c . |
(5) |
Пропорциональность времени прохождения τ оптической длине пути L дает возможность сформулировать принцип Ферма следующим образом:
свет распространяется по такому пути, оптическая длина которого минимальна.
Точнее, оптическая длина пути должна быть экстремальной, т. е. либо минимальной, либо максимальной, либо стационарной — одинаковой для всех
возможных путей. В последнем случае все пути света между двумя точками оказываются
таутохронными (требующими для своего прохождения одинакового времени).
Из принципа Ферма вытекает обратимость световых лучей. Действительно, оптический путь, который минимален в случае распространения света из точки 1 в точку 2, окажется минимальным и в случае распространения света в обратном направлении.
Получим с помощью принципа Ферма закон
Алек Власов. ЛЕКЦИИ ПО ФИЗИКЕ |
5 |
|
Оптика. Квантовые свойства излучения. Лекция № 2
отражения света.
|
|
Рис. 2. |
|
|
|
Пусть |
|
свет попадает |
из |
точки А в |
точ~ |
ку |
В, |
отразившись |
от |
поверхности |
MN |
(рис. 2; прямой путь из А в В прегражден непрозрачным экраном Э). Среда, в которой проходит луч, однородна. Поэтому минимальность оптической длины пути сводится к минимальности его геометрической длины.
Геометрическая длина произвольно взятого пути равна АО'В = А'О'В (вспомогательная точка А' является зеркальным изображением точки А1 . Из рисунка видно, что наименьшей длиной обладает путь луча, отразившегося в точке О, для которой угол отражения равен углу падения. Заметим, что при удалении точки О' от точки О геометрическая длина пути неограниченно возрастает,
так |
что |
в |
данном |
случае |
имеется только один экстремум — минимум. |
|
|||
Алек Власов. ЛЕКЦИИ ПО ФИЗИКЕ |
6 |
|
Оптика. Квантовые свойства излучения. Лекция № 2
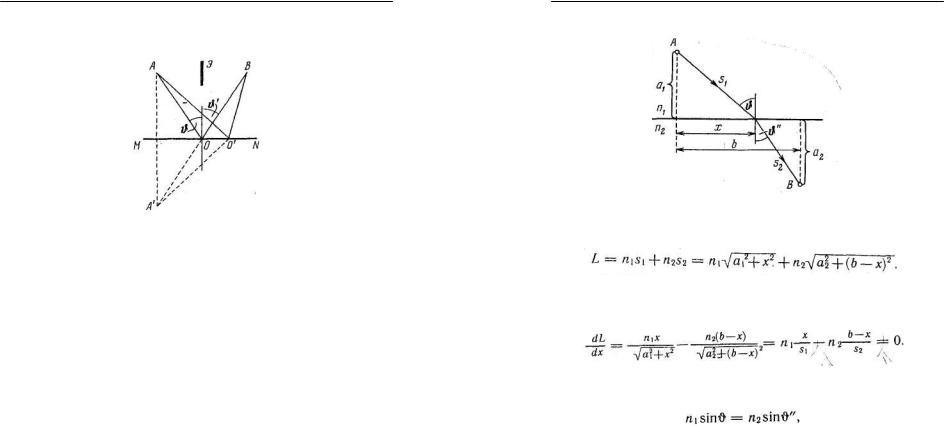
преломления света, рис. 3.
Рис. 3.
Для произвольного луча оптическая длина пути равна
Чтобы найти экстремальное значение, продифференцируем L по х и приравняем производную нулю:
Множители при n1 и п2 равны соответственно sinϑ и sin ϑ′′ . Таким образом, получается соотношение
выражающее закон преломления.
Получим с помощью принципа Ферма закон

Алек Власов. ЛЕКЦИИ ПО ФИЗИКЕ |
7 |
|
Оптика. Квантовые свойства излучения. Лекция № 2
3. ТАУТОХРОННЫЕ ЛУЧИ Рассмотрим отражение от внутренней поверхности
эллипсоида, рис. 4.
Рис. 4.
Здесь F1 и F2 — фокусы эллипсоида. В соответвии с опделением эллипса пути F1OF2 , F1O′F2 , F1O′′F2 и т. д. одинаковы по длине. Поэтому все лучи, вышедшие из фокуса F1 и пришедшие после отражения в фокус F2,
являются таутохронными. В этом случае оптическая длина пути стационарна.
Если заменить поверхность эллипсоида поверхностью ММ, имеющей меньшую кривизну и ориентированной так, рис. 4, что луч, вышедший из точки F1 , после отражения
от ММ попадает в точку F2, то путь F1OF2 будет минимальным.
Для поверхности NN, рис. 4, имеющей кривизну большую, чем у эллипсоида, путь F1OF2 будет максимальным.
Алек Власов. ЛЕКЦИИ ПО ФИЗИКЕ |
8 |
|
Оптика. Квантовые свойства излучения. Лекция № 2
Стационарность оптических путей имеет место также при прохождении лучей через линзу, рис. 5.
Рис. 5
Луч POP' имеет самый короткий путь в воздухе (где показатель преломления п практически равен единице) и самый длинный путь в стекле n ≈ 1,5 . Луч PQQ'P' имеет
более длинный путь в воздухе, но зато более короткий путь в стекле. В итоге оптические длины путей для всех лучей оказываются одинаковыми. Поэтому лучи таутохронны, а оптическая длина пути стационарна.
Равенство оптических длин означает равенство времён прохождения светом соответствующих путей.
В случае нарушения таутохронности на пути с разностью оптических длин δL возникает отставание по фазе световых колебаний, определяемое выражением
δϕ = − |
δL |
2π , |
(6) |
|
λ0
где λ0 – длина волны в вакууме.
Алек Власов. ЛЕКЦИИ ПО ФИЗИКЕ |
9 |
|
Оптика. Квантовые свойства излучения. Лекция № 2
4. ПРЕЛОМЛЕНИЕ У ОДНОЙ СФЕРИЧЕСКОЙ ПОВЕРХНОСТИ
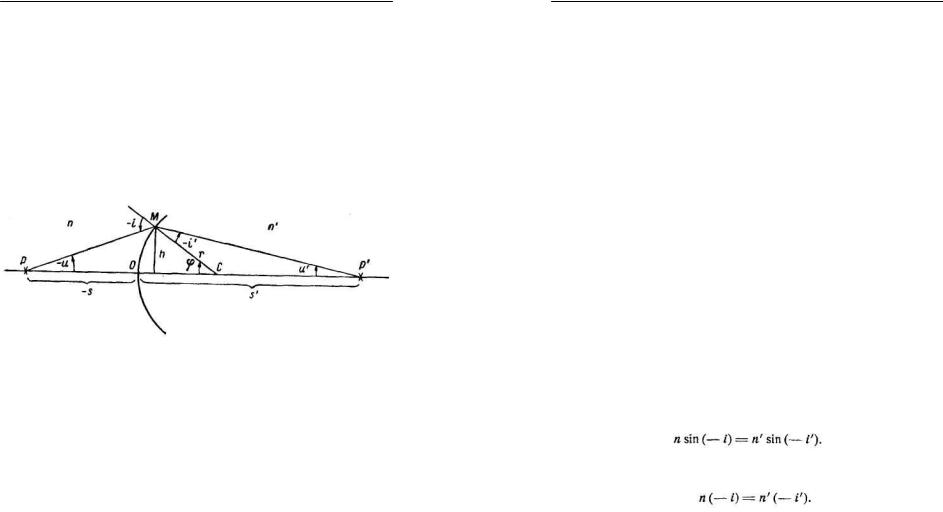
Пусть два однородных прозрачных вещества с коэффициентами преломления п и п' разделены сферической поверхностью с радиусом кривизны r .
Проведем главную оптическую ось, под которой подразумеваем прямую, проходящую через точечный источник света Р и центр кривизны поверхности С
(рис. 6).
|
Рис. 6. |
|
Будем |
пользоваться |
следующим правилом |
знаков: |
|
|
•длины отсчитываем от вершины преломляющей поверхности О считаем их положительными, если они направлены в сторону распространения света;
•углы отсчитываем от направления главной оптической оси (или нормали к сферической поверхности) и считаем их положительными, если они отсчитаны по часовой стрелке.
На чертежах будем всегда отмечать
Алек Власов. ЛЕКЦИИ ПО ФИЗИКЕ |
10 |
|
Оптика. Квантовые свойства излучения. Лекция № 2
положительные значения длин и углов. Например, если некоторая длина, отмечаемая буквой s , отрицательна, то на чертеже у соответственного отрезка поставим − s . Определим направление лучей, исходящих из точечного объекта Р, углами u , которые лучи составляют с главной оптической осью PC. Будем рассматривать только лучи, составляющие с оптической осью столь малые углы, что для них синусы
и тангенсы можно заменять самими углами, а
косинусы считать равными единице. Такие лучи носят название ПАРАКСИАЛЬНЫХ.
Рассмотрим луч, исходящий из объекта Р, падающий на границу раздела веществ в точке М и пересекающий после преломления главную оптическую ось в точке Р'. При соблюдении указанного правила знаков угол и, направление которого отмечено на рис. 6 стрелкой, отрицателен. Положительной будет величина − u . Углы падения и преломления i и i′ также отрицательны. Положительны величины − i и − i′ . По закону преломления:
Считая рассматриваемый луч параксиальным, заменим синусы через углы и тогда получим
(7)
Из треугольника PMC имеем: − i = ϕ − u и из треугольника СМР’ имеем: − i′ = ϕ − u′ , где —и и и' — положительные углы, которые составляют лучи РМ и МР' с главной оптической осью, и ϕ — положительный угол между той же осью и радиусом СМ. Подставляя

Алек Власов. ЛЕКЦИИ ПО ФИЗИКЕ |
11 |
|
|
Оптика. Квантовые свойства излучения. Лекция № 2 |
|
эти значения углов —i и — i ' в (7), найдем |
|
|
(8) |
Обозначив через —s и s' соответственно положительные расстояния от вершины преломляющей поверхности О до точек Р и Р' и через h — длину перпендикуляра, опущенного из точки М на ось PC, получим в рассматриваемом приближении:
Также для угла ϕ имеем
Подставляя эти значения —и, и' и ср в (2), найдем
(9)
или
(10)
Величина, стоящая в правой части выражения (10), зависит только от коэффициентов преломления рассматриваемых веществ и радиуса кривизны разделяющей их поверхности. Следовательно, для данных веществ и данной поверхности эта величина постоянна; она называется оптической силой преломляющей поверхности и обозначается буквой Ф:
(11)
или с учётом (10)
Алек Власов. ЛЕКЦИИ ПО ФИЗИКЕ |
12 |
|
|
Оптика. Квантовые свойства излучения. Лекция № 2 |
|
|
(12) |
При заданном положении объекта Р (заданном отрезке s) из формулы (12) получается определенное значение отрезка s', не зависимо от значения угла u .
Это означает, что при малых углах u все лучи, исходящие из точечного объекта Р, после преломления пересекаются в одной точке P′ . Для параксиальных лучей гомоцентрический пучок (т.е. выходящий из точки) в принятом приближении
остается после |
преломления |
у сферической |
||
поверхности |
гомоцентрическим; |
Р' |
является |
|
точечным изображением точечного объекта. |
|
|||
Из приведенных рассуждений ясно, что если |
||||
источник света поместить в точку P′ |
то точка Р станет |
|||
его изображением. Две точки Р и Р', удовлетворяющие тому условию, что если одна из них является объектом,
то |
другая — изображением, |
называются |
сопряженными. |
|
|
Ограничиваясь пока рассмотрением параксиальных лучей, найдем место, где соберется, после преломления у сферической поверхности пучок параллельных лучей. Для этого положим тогда по формуле (10):
(13)
Место, где пересекаются после преломления лучи, падавшие на сферическую поверхность в виде
Алек Власов. ЛЕКЦИИ ПО ФИЗИКЕ |
13 |
|
|
||
Оптика. Квантовые свойства излучения. Лекция № 2 |
|
|
параллельного пучка, называется вторым |
главным |
|
фокусом F' преломляющей поверхности, а |
расстояние |
|
от вершины преломляющей поверхности O до второго главного фокуса – вторым главным фокусным расстаянием f ′ . По (13) для f ′ получаем значение
(14)
Первым главным фокусом F преломляющей поверхности назовем точку, удовлетворяющую следующему условию: при помещении в эту точку точечного источника света Р после преломления должен возникнуть пучок параллельных лучей. Расстояние от вершины преломляющей поверхности О до первого главного фокуса называется первым главным фокусным расстоянием f . Для того чтобы определить
f , положим в формуле (10) |
s′ = ∞ , тогда получим |
|||
f = − |
n |
|
r . |
(15) |
|
|
|||
|
|
|||
|
n′ − n |
|
||
Алек Власов. ЛЕКЦИИ ПО ФИЗИКЕ |
14 |
|
|
Оптика. Квантовые свойства излучения. Лекция № 2 |
|
5. ТОНКАЯ ЛИНЗА
Оптической линзой называется тело, из- готовленное из однородного прозрачного вещества и ограниченное поверхностями, из которых, по крайней мере, одна имеет радиус кривизны, отличный от нуля.
Материалом для линз, употребляемых в видимом свете, служит стекло, а для линз, употребляемых в ультрафиолете, главным образом, кварц. Для инфракрасных лучей употребляются линзы из кварца, каменной соли, КС1 и т. д.
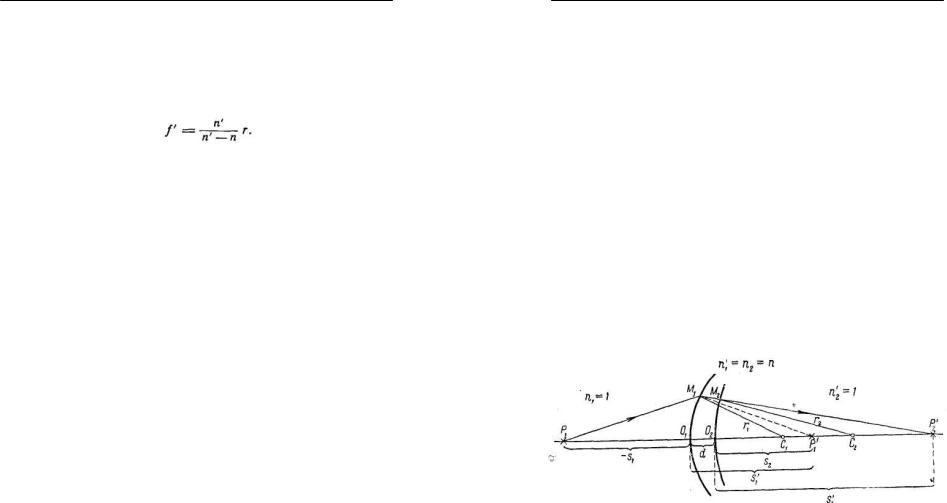
Преломление света в линзе можно рассматривать, как последовательное преломление у двух сферических поверхностей. Пусть О1 и О2 представляют собой две
сферические поверхности радиусов |
r |
и |
r , |
|
1 |
|
2 |
находящиеся на расстоянии d друг от друга (рис. 7).
Рис. 7.
Главной оптической осью системы поверхностей назовем прямую, проходящую через их центры С1 и С2. Между поверхностями пусть находится вещество с коэффициентом преломления п, а вне поверхностей

Алек Власов. ЛЕКЦИИ ПО ФИЗИКЕ |
15 |
|
|
Оптика. Квантовые свойства излучения. Лекция № 2 |
|
— воздух, коэффициент преломления которого будем считать равным единице. Отмечая величины, относящиеся к первой поверхности, индексом 1, а относящиеся ко второй поверхности — индексом 2, и придерживаясь в остальном обозначений, принятых выше, будем иметь
|
|
(16) |
При выполнении соотношения (16) получим |
||
|
|
(17) |
|
|
(18) |
Из рис. 7 видим, что между s |
2 |
и s′ имеет место |
|
1 |
|
соотношение:
Будем рассматривать тонкую линзу, т. е. такую линзу, для которойрасстояние d между ее преломляющими поверхностями мало по сравнению с расстояниями до
объекта и до изображения. Тогда приближенно s |
2 |
= s′ |
и |
||
|
|
1 |
|
||
из (17) получим |
|
|
|
|
|
Подставляя найденное таким образом значение |
n |
|
в |
|
|
s2 |
|
|
|||
|
|
|
|
||
(18), получаем
Алек Власов. ЛЕКЦИИ ПО ФИЗИКЕ |
16 |
|
Оптика. Квантовые свойства излучения. Лекция № 2
(19)
Рассматривая тонкую линзу, будем обозначать расстояния до объекта и изображения соответственно через s и s', тогда по (19) для тонкой линзы:
(20)
Формула (20) связывает положение объекта с положением изображения, даваемого тонкой линзой.
Для данной линзы заданы радиусы кривизны ее
поверхностей r |
и r и коэффициент преломления п |
1 |
2 |
вещества, из которого она сделана. Поэтому в правой части равенства (20) стоит постоянная величина
(21)
носящая название оптической силы линзы.
Легко видеть, что оптическая сила тонкой линзы равна сумме оптических сил ее обеих преломляющих поверхностей:
Φ = Φ1 + Φ2
Повторяя рассуждения, приведенные выше для одной преломляющей поверхности, найдем для фокусных расстояний тонкой линзы
|
|
|
|
(22) |
Коэффициент |
п > 1 |
всегда, |
следовательно, |
|
знак |
оптической силы |
Ф зависит от знака |
||
Алек Власов. ЛЕКЦИИ ПО ФИЗИКЕ |
17 |
|||||
|
||||||
Оптика. Квантовые свойства излучения. Лекция № 2 |
|
|||||
|
1 |
|
1 |
|
|
|
|
|
− |
|
|
Если Ф положительно, то мы |
|
|
|
|||||
величины |
r |
r |
. |
|||
|
|
|
|
|
||
1 |
|
2 |
|
|
||
имеем дело с собирательной {положительной)
линзой, — параллельный пучок света после преломления в линзе собирается в её главном фокусе.
Если Ф отрицательно, то мы имеем дело с рассеи-
вающей {отрицательной) линзой,— параллельный пучок света после преломления в линзе образует расходящийся пучок лучей, продолжения которых пересекаются во втором главном фокусе.
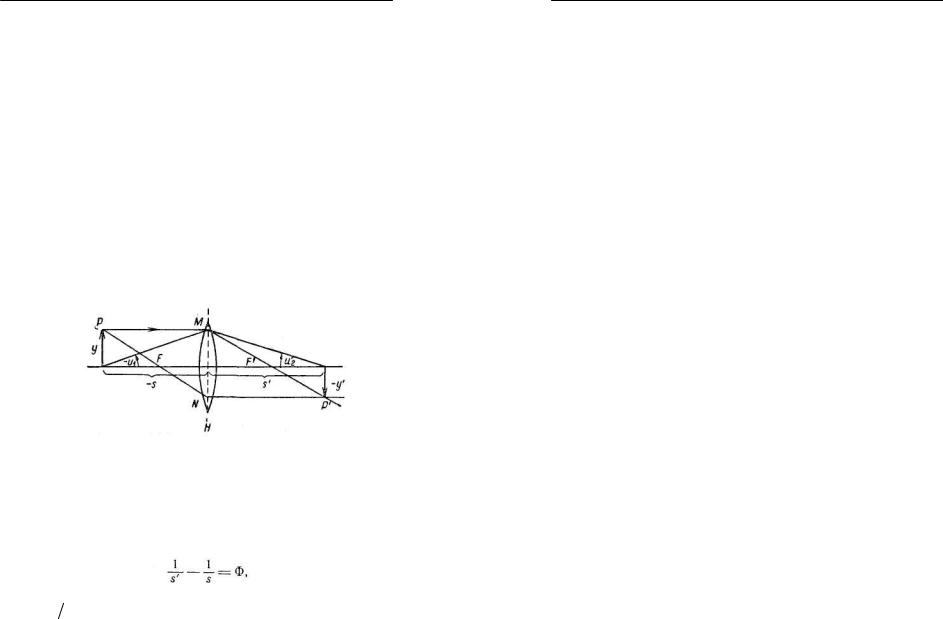
Изображение, даваемое тонкой линзой, показано на рис. 8.
Рис. 8.
Положение объекта у и изображения у' определяется отрезками s и s', отсчитанными от середины линзы (или от одной из ее вершин). Эти отрезки связаны между собой соотношением:
Алек Власов. ЛЕКЦИИ ПО ФИЗИКЕ |
18 |
||||||||||
|
|||||||||||
Оптика. Квантовые свойства излучения. Лекция № 2 |
|
||||||||||
Линейное увеличение, даваемое линзой, составляет |
|
||||||||||
β = |
y′ |
= |
|
u1 |
= |
s′ |
. |
|
|||
|
u′ |
|
|
||||||||
|
y |
|
|
|
|
|
s |
|
|||
|
|
2 |
|
|
|
|
|
|
|||
Угловое увеличение линзы составляет |
|
||||||||||
|
|
u′ |
1 |
|
|
|
|
||||
γ = |
2 |
= |
|
|
. |
|
|
||||
|
|
|
|
|
|||||||
|
|
|
u1 |
β |
|
||||||
где Φ = 1 f - оптическая сила линзы.
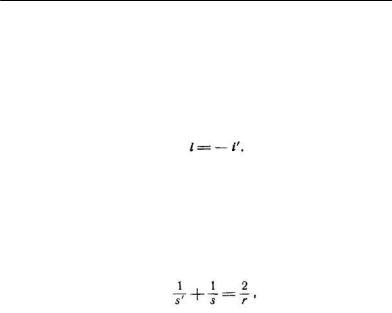
Алек Власов. ЛЕКЦИИ ПО ФИЗИКЕ |
19 |
|
|
Оптика. Квантовые свойства излучения. Лекция № 2 |
|
6. СФЕРИЧЕСКОЕ ЗЕРКАЛО Результаты, полученные для одной сферической
преломляющей поверхности, могут быть обобщены на случай сферического зеркала. Пусть i —угол падения и i′ —угол отражения. При соблюдении введенного нами правила знаков закон отражения имеет вид:
Формально этот закон получается из закона преломления (1), если коэффициент преломления п' положить равным —п. Отсюда и формулы, полученные для одной преломляющей поверхности, переходят в формулы для сферического зеркала, если в них положить п' = — п. Так, из формулы (10) получим
что позволяет по положению объекта найти положение изображения, .даваемого сферическим зеркалом.
Для главных фокусных |
расстояний зеркала |
|
имеем: |
|
|
f = f ′ = |
r |
|
|
|
|
2 |
|
|
Для вогнутого зеркала r > 0 и главный фокус F лежит перед зеркалом, посредине между его вершиной и центром кривизны. Для выпуклого зеркала r < 0 и главный фокус F лежит за зеркалом.
---------
