
random books / Соина, Казанцев, Васильева, Гольцман - Сборник вопросов и задач по ОФ Р3. Оптика. Р4. Квантовая физика (2013)
.pdf3.191. Дифракционная решетка имеет 20 000 штрихов при ее полной ширине 4 см. Какой будет дисперсия у такой решетки при освещении ее натриевой лампой ( = 589 нм) в спектре первого и второго порядков?
3.192. Угловая дисперсия дифракционной решетки для излучения с длиной волны 668 нм в спектре первого порядка равна 2,02 105 рад/м. Найдите период дифракционной решетки.
3.193. Найдите линейную дисперсию дифракционной решетки (см. задачу 3.192), если фокусное расстояние линзы, проецирующей спектр на экран, равно 40 см.
3.194. Определите для решетки, имеющей 3937 штрихов на 1 см: а) угловую дисперсию в спектре первого порядка; б) линейную дисперсию спектрографа при объективе с фокусным расстоянием 50 см; в) величину, обратную линейной дисперсии. Считать, что углы дифракции малы ( cos 1).
3.195. Какое расстояние между компонентами желтой линии дублета натрия ( 1 = 589 нм, 2 = 589,6 нм) получится на фотографическом негативе в спектрографе, в котором используется решетка, описанная в задаче 3.194?
3.196. В гониометре ГС5 используется дифракционная решетка, имеющая 600 штрихов на 1 мм длины. На каком расстоянии друг от друга будут находиться в фокальной плоскости объектива гониометра с такой решеткой две желтые линии излучения ртутной лампы ( 1 = 577 нм, 2 = 579 нм) в спектре первого порядка, если фокусное расстояние объектива зрительной трубы гониометра 27,3 см?
3.197. Определите угловое расстояние между главным максимумом и ближайшим к нему добавочным минимумом дифракционной решетки с периодом d и числом щелей N. (Удвоенное значение этой величины определяет угловую ширину спектральной линии в спектре, даваемом дифракционной решеткой.) Длина волны света . Считать, что углы дифракции малы.
3.198. Две дифракционные решетки имеют одинаковую ширину, но разное число штрихов (N1 > N2). Как отличаются у этих решеток дисперсии, разрешающие способности? Какая из них дает более узкие спектральные линии?
3.199. Изобразите зависимость от синуса угла дифракции интенсивности двух близких спектральных линий 1 и 2 в
41
спектре первого порядка для решеток: а) с одинаковыми дисперсиями и разными разрешающими способностями (R1 > R2); б) с разными дисперсиями (D1 > D2) и одинаковыми разрешающими способностями.
3.200. Длины волн спектральных линий обычно измеряют с точностью 0,0001 нм при помощи спектрографов, разрешающая способность которых составляет 0,001 нм. Почему это возможно?
3.201. Вычислите угловую ширину спектральных линий желтого дублета натрия ( 1 = 589 нм, 2 = 589,6 нм) для дифракционной решетки, рассмотренной в задаче 3.191. Будут ли разрешаться эти линии в первом порядке в спектрографе с такой решеткой?
3.202. Определите, каким должно быть минимальное число штрихов у дифракционной решетки, чтобы с ее помощью можно было видеть раздельно желтые линии излучения натриевой лампы в спектре первого порядка, если длины волн этих линий
1 = 589 нм, 2 = 589,6 нм.
3.203. Дифракционная решетка шириной 1 см имеет 50 штрихов на 1 мм. В каком наименьшем порядке спектра разрешаются две компоненты желтой линии натрия этой решеткой?
3.204. Найдите разрешающую способность R решетки шириной 4 см периодом 2 мкм в спектре первого порядка. Чему равна максимальная разрешающая способность такой решетки для желтой линии натрия ( = 589 нм)?
3.205. Покажите, что при нормальном падении света на дифракционную решетку максимально возможная разрешающая способность решетки не превышает значения L , где L – ширина решетки.
, где L – ширина решетки.
3.206. Дифракционная решетка шириной 3 см содержит 4000 штрихов на 1 см. Каким может быть минимальный интервал между двумя спектральными линиями, чтобы они были разрешены в спектре первого порядка, если = 589 нм? Может ли быть повышена разрешающая способность этой решетки для данной длины волны? Чему равен минимальный разрешаемый интервал длин волн min вблизи этой длины волны?
42
§3.5. ГЕОМЕТРИЧЕСКАЯ ОПТИКА
1.При переходе луча из среды 1 в среду 2 угол падения и угол преломления связаны соотношением:
|
sin |
|
n2 |
, |
|
sin |
|
n |
|
|
|
1 |
|
|
где n c |
– абсолютный показатель преломления среды, |
|||
v |
|
|
|
|
с – скорость света в вакууме.
2. Предельный угол полного отражения от оптически менее плотной среды (n2 < n1):
0 arcsin n2 . n1
3. Связь между преломляющим углом призмы и углом наименьшего отклонения:
sin 2 n sin 2 .
4. При преломлении на сферической поверхности, разделяющей среды с показателями преломления n и n’:
; увеличение nn' xx' ;
координатная ось 0х направлена по ходу светового пучка, начало координат совпадает с вершиной сферической поверхности, х и x’ – соответственно координаты источника и изображения, Rкр – координата центра кривизны поверхности.
5. При отражении от сферической поверхности
 ; увеличение xx' .
; увеличение xx' .
43
6. Формула тонкой линзы (начало координат находится в оптическом центре линзы):
1 |
|
1 |
|
1 |
n ' |
|
1 |
|
1 |
|
; увеличение |
x ' |
; |
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
||
|
|
|
|
|
|
x |
||||||||
x ' |
|
x |
|
F |
n |
|
R1 |
|
R2 |
|
|
|||
F – фокусное расстояние линзы, R1 и R2 – координаты центров кривизны первой и второй преломляющих поверхностей, n’ и n – показатели преломления линзы и окружающей ее среды соответственно.
Прямолинейность распространения света
3.207. В каких случаях можно пользоваться представлениями о световом луче?
3.208. Если вы видите глаза другого наблюдателя через сложную систему зеркал, сможет ли он, в свою очередь, видеть ваши глаза?
3.209. В какой среде лучи света могут быть криволинейными? 3.210. Заходящее Солнце кажется расположенным выше, чем
на самом деле. Как это объяснить? Поясните ответ рисунком. 3.211. Искусственный спутник Земли можно иногда долго
наблюдать после захода Солнца в виде движущейся ярко светящейся точки. Какова должна быть наименьшая высота спутника, обращающегося по круговой орбите в плоскости экватора, чтобы он был виден на экваторе прямо над головой через 2 ч после захода Солнца? Оцените, какую долю периода обращения Т этого спутника составляет время t, в течение которого спутник можно наблюдать при его движении от горизонта до зенита; выразите также время t в минутах.
3.212. Помня, что Луна видна в отраженном свете, объясните: а) почему, если Луна восходит на востоке в полночь, не может быть полнолуния; б) почему молодой месяц не может быть долго виден после наступления темноты? (Нарисуйте схемы расположения Солнца, Земли и Луны в ее различных фазах.)
3.213. Иногда мы наблюдаем полные, а иногда кольцеобразныезатменияСолнца. НачертивсхемурасположенияЗемли, Луны и Солнца, объясните, почему возможны оба вида солнечных затмений.
44
3.214. Диаметр фотосферы Солнца равен 1,39 106 км, расстояние Солнца от Земли составляет в среднем 1,5 108 км и меняется незначительно. Расстояние от центра Луны до поверхности Земли меняется от 3,57 105 до 3,99 105 км. Когда солнечное затмение бывает полным и когда кольцеобразным, если диаметр Луны равен 3480 км?
3.215. С помощью горящей свечи на стене наблюдают тень от вилки. Если держать вилку вертикально, то тень получается четкой – все зубцы хорошо видны. Если же вилку повернуть горизонтально, то тени отдельных зубцов сливаются в одно серое пятно. Объясните явление, пояснив ответ чертежом.
3.216. Впервые общий принцип геометрической оптики был сформулирован французским математиком и физиком П. Ферма примернов1662 г. иполучилназваниепринципаФерма. Согласно этому принципу из всех возможных путей, соединяющих две точки, свет выбирает тот путь, для прохождения которого требуется наименьшеевремя. Получитеспомощьюпринципа Фермазаконы отражения и преломления света.
Отражение и преломление света на плоской границе раздела сред
3.217. Как осветить дно колодца лучами Солнца, находящегося на высоте 60 над горизонтом?
3.218. В обычном плоском зеркале наше изображение оказывается перевернутым справа налево, то есть изображение правой руки выглядит как левая рука «человека» в зеркале. Почему зеркало не переворачивает все еще «вверх ногами»? Что действительно переворачивается зеркалом?
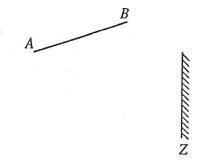
3.219. Плоское зеркало Z инекоторыйпредметАВрасположены так, как показано на рис. 19. Где должен располагаться глаз наблюдателя, чтобыпредметбылвиден целиком?
3.220. На рис. 20а–в па-
раллельный пучок монохроматического света входит в ящик слева. Что должно
45
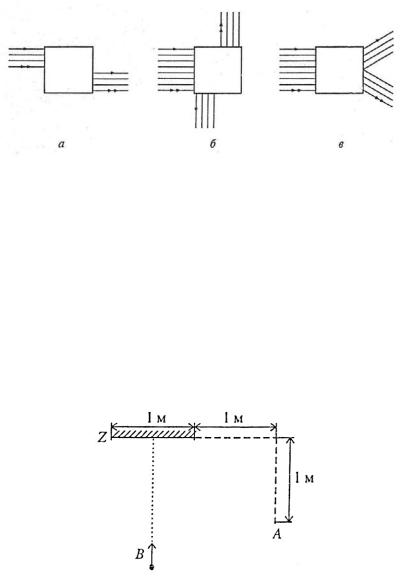
быть расположено в каждом ящике, чтобы выходящие пучки имеливид, показанныйнарисунке? Однаидвестрелкинавыходящих лучах соответствуют крайним лучам входящего пучка.
Рисунок 20
3.221. В магазинах готовой одежды нередко имеются зеркала, доходящие до самого пола, для того, чтобы покупатель мог видеть себя во весь рост. Обязательна ли для этого такая высота зеркала? Если самый низкорослый покупатель имеет рост около 150 см, то до какой высоты от пола можно поднять нижний край зеркала для того, чтобы все покупатели могли видеть в зеркале свою обувь?
3.222. Сбоку от зеркала Z (рис. 21) стоит человек А; второй человек В приближается к зеркалу по перпендикуляру, проходящему через середину зеркала. На каком расстоянии от зеркала будет находиться человек В в тот момент, когда оба человека смогут увидеть друг друга в зеркале?
Рисунок 21
46
3.223. Предмет высотой h = 0,5 м находится на расстоянии s1 = 2 м от плоского зеркала. Какова должна быть минимальная высота плоского зеркала, чтобы человек, находящийся на расстоянии s2 = 5 м от зеркала, мог видеть этот предмет полностью, если предмет расположен параллельно зеркалу?
3.224. Определите минимальную ширину нижнего зеркала перископа, при которой в нем будет видно полностью верхнее зеркало, если ширина верхнего зеркала равна 10 см, расстояние между верхним и нижним зеркалами равно 75 см, глаз находится на расстоянии 25 см от нижнего зеркала.
3.225. Пучок света падает на поверхность стола под углом30 . Под каким углом к горизонту надо поместить плоское зеркало, чтобы после отражения от него пучок света был параллелен поверхности стола?
3.226. Небольшой предмет расположен между двумя плоскими зеркалами, поставленными друг к другу под углом 30 на расстоянии r = 10 см от линии пересечения зеркал ближе к одному из зеркал. На каком расстоянии х друг от друга находятся первые мнимыеизображенияпредметавзеркалах? Каксместитсясередина отрезка прямой, соединяющей два изображения предмета, если предмет сдвинуть на = 2 см так, чтобы его расстояние от линии пересечения зеркал осталось неизменным?
3.227. Параллельный пучок света падает на одно из зеркал, составляющих двугранный угол 20 , параллельно плоскости, делящей угол пополам, под прямым углом к линии пересечения зеркал. Как он идет дальше? Каков будет световой поток по выходе пучка из двугранного угла, если световой поток на входе равен 600 лм и если при каждом отражении световой поток уменьшается в 2 раза?
3.228. Три плоских зеркала расположены взаимно перпендикулярно. Покажите, что луч, упавший под произвольным углом на одно из зеркал и отразившийся на второе, а затем на третье зеркало, после трех отражений идет антипараллельно прежнему направлению.
3.229. Точечный источник S (рис. 22), сила света которого I0, находится над горизонтальной плоскостью на высоте SM = h. Сбоку от него расположено плоское зеркало Z, отражающее свет в точку М. Определите освещенность в точке М, если SM = SZ, а коэффициент отражения зеркала равен R.
47

Рисунок 22
3.230. Ныряльщик видит Солнце из воды на угловом расстоянии 30 от зенита. На какой высоте над горизонтом находится Солнце?
3.231. Высота Солнца над горизонтом равна 20 . Человек, стоя на берегу пруда, с помощью плоского зеркала пускает зайчик в воду. Как надо расположить зеркало, чтобы отраженный от него луч шел в воде под углом 60 к горизонту?
3.232. Луч света падает на плоскопараллельную стеклянную пластинку под углом 60 . Какова толщина пластинки d, если при выходе из нее луч сместился на s = 20 мм?
3.233. Параллельный пучок света проходит сквозь несколько прозрачныхплоскопараллельныхпластин. Прикаждомпреломлении теряется 0,1 часть светового потока; внутри каждой пластины поглощается 0,2 светового потока. Каким будет световой поток, прошедший сквозь 5 пластин, если начальный световой поток равен 500 лм?
3.234. Для определения показателя преломления жидкости на дно сосуда положили линейку с делениями. Две щели, через ко-
|
торые рассматривают деления на |
|
линейке, при отсутствии жидко- |
|
стивсосудерасположенытак, что |
|
через них видно нулевое деление |
|
линейки (рис. 23). При заполне- |
|
нии сосуда слоем исследуемой |
|
жидкости высотой 10 см, если |
Рисунок 23 |
смотреть через щели в том же на- |
48
правлении, видно деление, соответствующее 8,6 см. Направление, под которым рассматриваются через щели деления на линейке, образует с поверхностью воды угол, равный 30 . Пользуясь этими данными, определите показатель преломления жидкости.
3.235. Свая, вбитая в дно реки, выступает из воды на 0,5 м. Определите длину тени сваи на дне реки в солнечный день, если лучи Солнца падают на поверхность воды под углом 60 и глубина реки в окрестности сваи 0,5 м.
3.236. Лучсветападаетподугломαнаплоскуюграницусреды с показателем преломления п. Как должны быть связаны между собой α и п, чтобы отраженный луч был перпендикулярен к преломленному?
3.237. Под стеклянной пластинкой толщиной d = 15 см лежит маленькая крупинка. На каком расстоянии от верхней поверхности пластинки образуется ее видимое изображение, если луч зрения перпендикулярен к поверхности пластинки?
3.238. Человек смотрит на свое изображение в зеркале, положенном на дно сосуда, наполненного водой. На какое расстояние аккомодирован глаз человека, если он находится на высоте 10 см над уровнем воды, а зеркало – на глубине 8 см под уровнем воды?
3.239. Предмет находится на расстоянии 1 = 15 см от плоскопараллельной стеклянной пластинки толщиной d = 4,5 см. Наблюдательрассматриваетегочерезпластинку, причемлучзрениянормален к ней. Определите, на каком расстоянии 2 от ближайшей к наблюдателю поверхности пластинки находится изображение
предмета. Каково кажущееся при- |
|
ближение предмета к наблюдате- |
|
лю, производимое пластинкой? |
|
3.240. Для определения пока- |
|
зателя преломления тонких про- |
|
зрачных пластинок микроскоп |
|
устанавливают так, чтобы отчет- |
|
ливобылвиденкакой-либообъект |
|
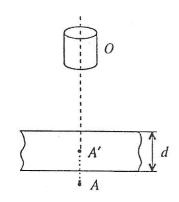
А. Затем между объектом и объек- |
|
тивом микроскопа О помещают |
|
испытуемую пластинку толщи- |
|
ной d (рис. 24). Тубус микроскопа |
|
поднимают на некоторую высоту |
Рисунок 24 |
49
, чтобывновь отчетливо видеть объект, который теперькажется находящимся в точке A’. Докажите, что n d (d ) .
(d ) .
3.241. Модификацией метода определения показателя преломления, описанного в задаче 3.240, является следующий. На верхнюю сторону плоскопараллельной пластинки наносят небольшое пятно, на которое и наводят микроскоп. Затем тубус микроскопа опускают на такое расстояние , чтобы в микроскоп было видно зеркальное изображение пятна в нижней поверхности пластинки. Получитеформулудлярасчетапвэтомметоде, еслитолщинапластинки равна d.
3.242. Плоскую стеклянную пластинку толщиной 3 мм рассматривают в микроскоп. Сначала микроскоп устанавливают для наблюдения верхней поверхности пластинки, а затем смещают тубус микроскопа вниз до тех пор, пока не будет отчетливо видна нижняя поверхность пластинки (для удобства наблюдения на поверхностях пластинки сделаны метки). Смещение тубуса оказалось равным 2 мм. Найдите показатель преломления стекла.
3.243. Учитывая, что показатель преломления алмаза равен 2,42, а стекла – 1,5, объясните, почему бриллиант блестит больше, чем его имитация из стекла при той же огранке.
3.244. Сероуглерод налит в широкий сосуд до высоты 10 см, считая от дна. В центре дна сосуда помещен источник света небольших размеров. Найдите площадь поверхности сероуглерода, через которую свет выходит в воздух.
3.245. Водолаз, находящийся на дне моря на глубине h = 6 м, смотритвверхивидитизображениекамней, лежащихнаднеморя. Определите, на каком минимальном расстоянии s от него лежат на дне видимые им камни.
3.246. В воде идут два параллельных луча 1 и 2 (рис. 25). Луч 1 выходитввоздухнепосредственноизводы, алуч2 проходитсквозь горизонтальную плоскопараллельную стеклянную пластинку. Будут ли лучи 1 и 2 параллельны по выходе в воздух? Выйдет ли в воздух луч 2, если луч 1 испытывает полное отражение?
3.247. Широкийпараллельныйпучоксвета, спектркоторогосодержит две длины волны 1 и 2 , распространяется в некоторой жидкостиспоказателемпреломленияnж. Какотделитьлучиразных длинволнспомощьютонкойпрозрачнойплоскопараллельнойпластинки, если показатель преломления вещества пластинки меньше, чем nж, и его значения различны для длин волн λ1 и λ2?
50
