электромагнитное поле определяется некоторым волновым процессом, поэтому об электромагнитном поле говорят как об электромагнитной волне. Таким образом, электромагнитной волной называют связанные колебания электрического и магнитного полей, причем связь между электрическим и магнитным полями осуществляется посредством уравнений Максвелла ( см. ниже формулы (1.10), (1.11)).

1.2. Плоские монохроматические волны

В электродинамике и оптике большое значение имеют плоские монохроматические волны. Электромагнитная волна называется монохроматической , если она зависит от времени по гармоническому закону.

Волна называется плоской, если она зависит только от одной пространственной координаты (см.(1.13)). Плоскую монохроматическую волну можно записать в виде

Постоянный вектор Em называется амплитудным вектором. Величину ψ называют фазой колебаний, ω - круговой или циклической частотой, постоянный вектор k – волновым вектором, α - начальной фазой.

ωT = 2π

Величина ν = 1/T называется частотой колебаний ( ν определяет число колебаний векторов E, H в фиксированной точке пространства за 1с ).

10

Размер λ характеризует пространственный период распределения полей E и H в плоской монохроматической волне в фиксированный момент времени ( см. рис.1.1).

Волновой вектор k указывает на направление распространения электромагнитной волны. Действительно, из первого уравнения Максвелла в (1.2) следует E k = 0. Поэтому E k . Разыскивая вектор Н в виде

H = Hm cos ψ,

для неизвестного амплитудного вектора Hm из второго уравнения в (1.1) получим

µµ0

Беря по модулю это соотношение, с учетом (1.8) получим следующую связь между амплитудами электрического и магнитного полей

Из (1.10)следует, что H k , H E . Таким образом, векторы H , E, k взаимно ортогональны. Это обстоятельство позволяет изобразить картину распространения волны в виде, указанном на рис.1.1, откуда видно, что волна движется вдоль вектора k.

Е

λЛуч света

k

H

Рис.1.1. Пространственная картина распределения напряженностей электрического и магнитного полей в плоской монохроматической волне

11

Вектор плотности потока энергии электромагнитного поля в плоской монохроматической волне выражается как

Отсюда видно, что плотность потока энергии электромагнитного поля совпадает с направлением движения электромагнитной волны. Направим ось x вдоль вектора k . Тогда

координата точки поверхности фронта волны x является функцией времени, а производная dx/dt будет скоростью волны.

Дифференцируя соотношение (1.13), с учетом (1.8), получим

dx/dt = ω /k = v

Таким образом, v - это скорость распространения электромагнитной волны в среде. В вакууме ε = µ = 1, поэтому

v = c =1 / ε0µ0 = 3×108 м/ с

Величину

называют абсолютным показателем преломления среды. Отметим что между частотой ν , длиной волны λ и скоростью света в среде v имеют место следующие соотношения:

Первая формула являются следствиями дисперсионного соотношения

(1.8).

1.3. Основные характеристики света

12

Чтобы определить понятие "короткие электромагнитные волны", обратимся к шкале электромагнитных волн

Из таблицы видно, что коротковолновая часть спектра определяет

Электрические колебанияλ

световые волны с длинами ~ 1 мкм. ЕслиМолекуляговоритьн – атомныеточныхколебаниязначениях,

вибраторов

то частоты и длины световых волн определяются значениями

0,39 мкм ≤ λ ≤ 0,76 мкм, ν = (0,4 − 0,75) 1015 Гц

Электромагнитные вволны этого диапазона называются светом потому, что они воспринимаются человеческим глазом. Выделенный

диапазон световых волн является условным, так как глаз человека реагирует не только на частоту колебаний. но и на интенсивность. По этой причине можно наблюдать яркое свечение лазерного луча с длиной волны 0,85 мкм.

Уместно отметить, что глаз человека наиболее восприимчив к свету с длиной волны 0,555 мкм ( зеленый свет ) и именно эта часть спектра света в оптическом диапазоне наиболее интенсивно излучается Солнцем.

Для большинства оптически прозрачных сред ( то есть пропускающих свет ) имеет место µ ~ 1 , поэтому можно считать

Опыт показывает, что диэлектрическая проницаемость среды является функцией частоты электромагнитного поля ε = ε(ν). Типичная частотная

зависимость ε(ν) представлена на рис. 1.2.

13

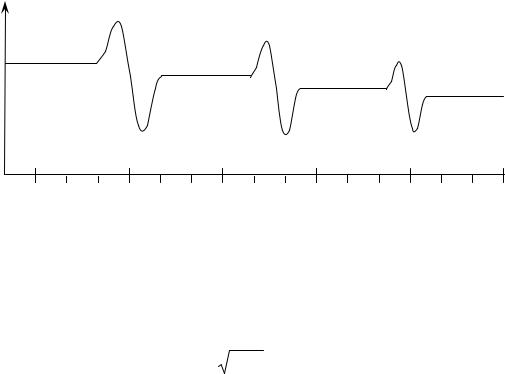
ε

Рис. 1.2. Частотная зависимость ε(ν) : ε нч - низкочастотная; ε рч - радиочастотная; ε ин - инфракрасная; εопт - оптическая

Данные на рис.1.2 показывают, что формулу (1.16) следует писать в виде

поляризации вещества и объясняется теорией поляризации диэлектриков

[1].

Всилу того, что скорость света в вакууме всегда больше скорости света

всреде с > v , значения показателей преломления различных сред больше единицы n > 1.

Опыт показывает, что взаимодействие света с веществом обусловливается в основном только взаимодействием с электрическим полем электромагнитной волны, то есть с вектором Е. По этой причине вектор Е называют световым вектором.

Согласно (1.6) электромагнитное поле переносит энергию. Так как частота изменения электромагнитного поля чрезвычайно велика, то измерительные приборы (и глаз человека ) обычно фиксируют среднюю величину модуля потока энергии, определяемого как

где t0 - время наблюдения волны, которое значительно больше периода колебаний t0 >> Т = 1/ ν.

Средний модуль плотности потока электромагнитной энергии называют интенсивностью света и обозначают как I :

I = < | S | >

14

Используя связь (1.11) между амплитудами получаем следующее выражение для интенсивности плоского монохроматического света

ради удобства обозначений для амплитуды светового вектора будем пользоваться различными обозначениями: Em , A, E0 , b и так далее. Обратим внимание, что интенсивность света зависит только от амплитуды волны и характеристик среды, но не зависит от частоты света ( или его длины волны ).

Упражнение. Используя формулы (1.7) и (1.12), доказать справедливость соотношений (1.19).

Свет называется естественным , если электромагнитная волна является суперпозицией ( суммой ) волн различной длины и различной ориентации световых векторов.

Свет называется поляризованным, если вдоль луча световой вектор каким либо образом упорядочен. Например, в случае плоской монохроматической волны световой вектор находится в плоскости, проходящей через луч и световой вектор. В этом случае свет называют плоскополяризованным. Если конец светового векра описывает вдоль луча винтовую линию, то его такую волну называют эллиптически поляризованной. Эллиптическая поляризация света имеет место при прохождении через растворы, содержащие органические вещества, например, в растворах сахара.

Линия, вдоль которой распространяется световая энергия, называется лучом. Из определения следует, что вектор плотности потока световой энергии S является касательным к лучу ( рис.1.3 ). Если исходить

Ei

Рис.1.3.Световые векторы Ei , суперпозиция которых образует белый свет, ортогональны направлению луча естественного (белого) света

15

В системе СИ характеристики электромагнитного излучения имеют следующие единицы измерения.

Приведем значения показателей преломления некоторых прозрачных сред

Таким образом, к основным характеристикам света относят такие понятия: частота и длина волны света, понятие монохроматического, естественного и поляризованного света, интенсивность, луч, волновой вектор и волновое число, дисперсионное соотношение ( связывающее частоту и длину волны света ), световой вектор и его ориентация относительно луча.

ЗАДАЧИ. Задача 1.1.

Длина волны монохроматического света в вакууме равна λ0 =0,5 мкм.

Найти частоту и длины волн этой световой волны в воде и стекле. Решение. Частота колебании света согласно (1.15) выражается как v = c / n = 3 108 (м/ c) / 0,5 10−6 (м) = 6 1014 Гц. При переходе из одной

среды в другую не изменяется частота света и изменяется скорость света согласно v = c/n и длина волны. Отсюда получаем v = c / λ0 = c /(nλ) , что

дает λ = λ0 / n . В случае воды λ = 0,5 мкм / 1,33 = 0,376 мкм, стекла

λ = 0, 333 мкм.

16