
random books / Паршаков А.Н. - Принципы и практика решения задач по общей физике. Часть 3_ Оптика. Квантовая физика
.pdf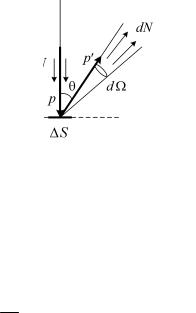
числа фотонов в направлении dΩ отража- |
|
|
|
|||||
|
|
|
||||||
ется dN = ∆N dΩ фотонов, где |
∆N = |
I∆S |
, |
|
|
|
||
|
|
|
|
|
||||
2π |
|
|
ω |
|
|
|
||
а в качестве элементарного телесного угла |
|
|
|
|||||
удобно взять dΩ = 2πsin θdθ (мы проин- |
|
|
|
|||||
тегрировали истинный элементарный те- |
|
|
|
|||||
лесный угол в сферической системе коор- |
|
|
|
|||||
динат dΩ = sin θdθdϕ по азимутальному |
|
|
|
|||||
углу ϕ от нуля до 2π). Число ежесекунд- |
|
Рис. 3.5 |
||||||
но падающих на площадку ∆S фотонов |
|
|
|
|||||
с энергией ω находится как |
∆N = |
I∆S |
. |
Проекция изменения им- |
||||
|
||||||||
|
|
|
ω |
|
|
|
||
пульса каждого из этих отраженных фотонов на направление, перпендикулярное площадке ∆S (нас интересует именно это значение), определяется по формуле
∆p = p(1+cos θ) = cω(1+cosθ) .
Тогда согласно второму закону Ньютона
dF = ∆p dN = |
I∆S |
(1+cos θ)sin θdθ, |
|
|
|||
|
|
c |
|
|
|
||
что после интегрирования по углу θ от нуля до π/ 2 дает |
|||
|
F = 3I∆S . |
||
|
|
2c |
|
Соответственно для всей поверхности S имеем F = 3IS / 2c. |
|||
Этот результат можно было предугадать заранее, так как абсолютно матовая поверхность занимает промежуточное положение между плоской зеркальной поверхностью и абсолютно черной.
3. Свет от точечного изотропного источника мощностью P падает на идеально зеркальную пластинку радиусом R. Источник находится над центром пластинки на расстоянии l от нее (рис. 3.6).
171

Симметрия задачи говорит о том, что в качестве бесконечно малой элементарной площадки dS следует вы-
|
|
брать |
тонкое |
кольцо |
радиусом |
r |
|
|
и толщиной dr |
с центром под источ- |
|||
|
|
ником света. В предыдущих задачах |
||||
|
|
|||||
|
|
было показано, что сила давления не |
||||
|
|
зависит от спектрального состава излу- |
||||
|
|
чения, поэтому будем полагать, что все |
||||
|
|
фотоны |
имеют |
одинаковую энергию |
||
|
|
ω. Тогда полное число фотонов, |
рас- |
|||
Рис. 3.6 |
|
|||||
|
|
пространяющихся ежесекундно от ис- |
||||
точника мощностью |
P во всех направлениях, N = P / |
ω. Из этого |
||||
числа в направлении площадки dS, которая видна под телесным углом dΩ = 2πsin θdθ, летит dN = (N / 4π)dΩ фотонов. Изменение импульса одного фотона составляет ∆p = 2( ω/ c)cos θ. Таким образом, сила давления на элемент dS согласно второму закону Ньютона
dF = ∆pdN = Pc sin θcosθdθ.
Осталось только проинтегрировать по углу θ от нуля до некоторого максимального угла θm , определяемого условием
sin θm = |
R |
. |
||||
|
|
|||||
R2 |
+l2 |
|||||
|
|
|
|
|||
В итоге получаем |
|
|
|
|
|
|
F = |
|
P |
|
|
. |
|
|
||||||
2c(1+l2 / R2 ) |
||||||
3.2.4. Фотоэффект. Никелевый шарик, играющий роль внутреннего электрода сферического вакуумного фотоэлемента, освещают моноэнергетическим электромагнитным излучением различных
172
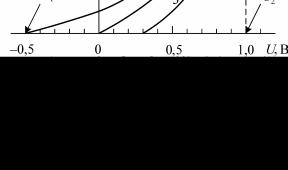
длин. Полученные вольт-амперные характеристики представлены на рис. 3.7 (данные характеристики построены в таком масштабе, что значение тока насыщения во всех случаях оказалось одинаковым). Найти с помощью этих графиков соответствующие длины волн.
Рис. 3.7
Очевидно, искомую длину волны можно найти только из уравнения Эйнштейна для фотоэффекта, записанного через длину волны:
2π c |
= A + |
1 mvm2 |
, |
(1) |
λ |
|
2 |
|
|
где A – работа выхода (для никеля А = 4,84 эВ); |
vm – максимальная |
|||
скорость фотоэлектронов, которой соответствует максимальная кинетическая энергия. Казалось бы, что для ее определения достаточно измерить задерживающую разность потенциалов Uз, т.е. определить
показания вольтметра, при которых ток фотоэлемента обращается в нуль. Именно так обстоит дело, если катод и анод фотоэлемента изготовлены из одного материала. Если же эти электроды изготовлены из разных материалов (что обычно и бывает), то определение задерживающей разности потенциалов усложняется. В этом случае начинает играть заметную роль контактная разность потенциалов, возникающая при контакте разных металлов (катод и анод образуют единую цепь). Причем контактная разность потенциалов определяется разностью работ выхода электронов из материала катода и анода
173
и не зависит от материала промежуточных проводников. Если бы контактной разности потенциалов не было, то при напряжении между катодом и анодом, равным нулю, все фотоэлектроны вне зависимости от начальной скорости достигали бы анода, и мы уже имели бы ток насыщения.
Наличие контактной разности потенциалов приводит к сдвигу вольт-амперной характеристики по оси U , зависящему от знака контактной разности потенциалов. Если ее знак таков, что она тормозит вылетающие из катода электроны, то приходится прикладывать внешнее напряжение, компенсирующее тормозящую контактную разность потенциалов, и начало горизонтального участка (ток насыщения) сдвигается вправо в сторону положительных значений показания вольтметра. Если же контактная разность потенциалов не тормозит, а ускоряет фотоэлектроны, то вольт-амперная характеристика фотоэлемента смещается влево. Очевидно, в обоих случаях значение задерживающего напряжения можно найти как
Uз =U2 −U1,
где значение U2 соответствует напряжению, при котором устанавливается ток насыщения, а значению U1 соответствует нулевой ток фо-
тоэлемента (см. рис. 3.7). Отметим, что положение точки 2 зависит только от контактной разности потенциалов, положение же точки 1 – от частоты падающего света. Значит, и задерживающая разность потенциалов Uз тоже зависит от частоты падающего света. Определив
Uз, мы тем самым находим максимальную кинетическую энергию фотоэлектронов
12 mvm2 = eUЗ = e(U2 −U1 ).
Подставляя это выражение в (1), находим
λ = |
2π c |
|
|
, |
|
A +e(U2 −U1 ) |
||
174
что после подстановки численных значений дает λ, равную 196, 213
и224 нм.
3.2.5.Рентгеновское излучение. В сплошном рентгеновском
спектре интенсивность излучения Iλ с длиной волны λ0 = 50 пм зависит от напряжения U на рентгеновской трубке следующим образом: при напряжениях U , равных 29, 28, 27, 26 (кВ), значение интенсивности Iλ в относительных единицах составляло соответственно
10,0; 6,0; 3,0 и 1,4 единиц. Вычислить по этим данным постоянную Планка .
Метод определения постоянной Планка, основанный на измерении коротковолновой границы тормозного рентгеновского излучения, является наиболее точным. Его называют методом изохромат. Заключается этот метод в том, что спектрометр для рентгеновского излучения устанавливают так, чтобы в счетчик попадало излучение одной и той же определенной длины волны, и измеряют интенсивность Iλ в зависимости от приложенного к рентгеновской трубке на-
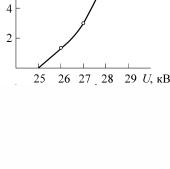
пряжения U. Построим эту зависимость, используя данные в задаче условия, и экстраполируем ее до пересечения с осью абсцисс.
Из рис. 3.8 находим значение соответствующего напряжения U0 = 25 кВ,
при котором значение Iλ обращается в нуль. При этом напряжении излучение с длиной волны λ0 = 50 пм стано-
вится коротковолновой границей сплошного рентгеновского спектра. Это, конечно, не означает, что рентгеновское излучение исчезает – исчезает излучение с этой длиной волны, а остается излучение с бóльшими длинами волн. В данном случае энергия свето-
вых квантов ω значительно превышает работу выхода A и тогда уравнение Эйнштейна принимает более простой вид
175

ω= 12 mvm2 .
Эту формулу можно интерпретировать и иначе: не как переход энергии светового кванта в кинетическую энергию электрона, а наоборот, как переход кинетической энергии электронов, ускоренных разностью потенциалов U , в энергию квантов, возникающих при резком торможении электронов в материале антикатода. По этой причине процесс возникновения рентгеновских квантов называют иногда обратным фотоэффектом.
Приравнивая кинетическую энергию электронов работе электрического поля через ускоряющее напряжение, получаем
2π c = eU0.
λ0
Эта формула определяет минимальную длину волны, с которой могут испускаться рентгеновские лучи при заданном напряжении на трубке. В нашем случае λ0 = 50 пм, U0 = 25 кВ. Используя эти данные, находим
=2eλπ0c U0 =1,06 10−34 Дж с.
3.2.6.Взаимодействие фотона с атомом. Фотон с длиной вол-
ны λ =17,0 пм вырывает из покоящегося атома электрон, энергия
связи которого Eсв = 69,3 кэВ. Найти импульс, переданный атому
в результате этого процесса, если электрон вылетает под прямым углом к направлению налетающего фотона.
При взаимодействии фотона с электроном атома последний получает практически всю энергию фотона, так как масса атома много больше массы электрона. Импульс же, который получает атом pа,
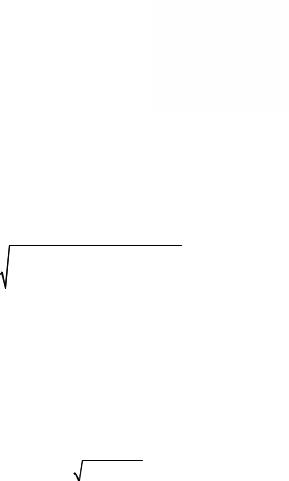
можно найти из закона сохранения импульса (рис. 3.9): pe2 + pф2 = pа2 , где pф – импульс фотона, pф = ω/ c; pe – импульс электрона. Для
176
его определения нам следует решить: какой формулой (релятивистской или нерелятивистской) связан импульс электрона с его энергией? Обратимся к закону сохранения энергии
ω= Ee + Eсв → Ee = ω− Eсв |
|
и оценим величину ω= 2πc / λ ≈ 72,9103 эВ. |
Рис. 3.9 |
Тогда с учетом Eсв = = 69,3 кэВ электрону |
|
достанется около 3,6 103 |
эВ, что гораздо меньше его энергии покоя |
|||||||||
(≈ 0,51 МэВ). |
Поэтому |
воспользуемся нерелятивистской |
связью |
|||||||
энергии и импульса p2 |
= 2m( ω− E ). Таким образом, |
|
||||||||
|
|
e |
|
|
св |
|
|
|
|
|
|
p = 1 |
2π 2 |
+ 2mc2 2πc − E |
|
, |
|
||||
|
a |
c |
|
|
|
λ |
св |
|
|
|
|
|
|
λ |
|
|
|
|
|
||
что составляет |
примерно 95 |
кэВ/ c. |
Здесь c |
|
– |
скорость |
света, |
|||
ане секунда (так часто выражают импульс микрочастиц).
3.2.7.Взаимодействие фотона со свободным электроном. По-
казать, что свободный электрон не способен поглощать и испускать фотоны.
Чтобы понять это, рассмотрим с точки зрения законов сохранения энергии и импульса процесс поглощения фотона свободным покоящимся электроном. Из закона сохранения энергии следует
ω+mc2 = c p2 + m2c2 ,
где p – импульс электрона после поглощения фотона. В силу закона
сохранения импульс электрона должен быть равным импульсу поглощенного фотона p = ω/ c. После подстановки этого значения
в закон сохранения энергии и возведения в квадрат, приходим к равенству 2 ω mc2 = 0, что, очевидно, невозможно, так как ни ω, ни m не равны нулю. В силу эквивалентности различных инерци-
177
альных систем отсчета получаем, что и движущийся свободный электрон не способен поглотить фотон. Нетрудно понять, что свободный электрон не имеет права и излучать фотон (этот процесс является обратным поглощению).
Полученный результат в некотором смысле тривиален. Наше доказательство молчаливо предполагало, что масса электрона до и после взаимодействия остается той же самой. Это значит, что внутреннее состояние электрона при этом не изменяется. В этом случае полная энергия электрона при испускании фотона может только возрастать за счет отдачи во время испускания. Испущенный фотон в свою очередь несет положительную энергию. И если бы испускание фотона было возможно, то оно сопровождалось бы нарушением закона сохранения энергии.
В то же время при рассмотрении фотоэффекта мы полагали, что свободный электрон может полностью поглотить фотон. Не противоречит ли это только что доказанному утверждению о невозможности поглощения или испускания фотона свободным электроном? На самом деле никакого противоречия нет. Оно возникает из-за неудачной терминологии. «Свободный электрон в металле» на самом деле не свободен. Для электрона металл является потенциальной ямой. И фотон взаимодействует не только с электроном, но и со всем металлом в целом. Импульс фотона воспринимается как электроном, так и металлом, энергия же фотона передается только электрону, так как масса металла может считаться бесконечно большой. Напротив, упругое рассеяние фотона свободным электроном (или который может считаться таковым) вполне возможно; это наблюдается при эффекте Комптона.
3.2.8. Эффект Комптона. Рассмотрим две задачи.
1. Фотон с энергией ω рассеялся под углом θ на покоившемся свободном электроне. Определить угол ϕ, под которым вылетел
электрон отдачи (по отношению к направлению налетевшего фотона). На рис. 3.10 отображен закон сохранения импульса при рассея-
нии фотона на свободном электроне k = k′+ p. Здесь k – им-
178

пульс налетающего фотона (его модуль ра-
вен |
ω/ c), |
k′ – импульс рассеянного фо- |
|
|||||
тона, |
p – |
импульс электрона отдачи. |
Из |
|
||||
рис. 3.10 находим |
|
|
|
|
|
|||
|
tg ϕ = |
k′sin θ |
= |
sin θ |
|
(1) |
|
|
|
k −k′cos θ |
λ′/ λ−cosθ |
||||||
|
|
|
|
|
Рис. 3.10 |
|||
|
|
|
|
|
|
|
|
|
(при выводе данного соотношения мы вос-
пользовались тем, что k = 2π/ λ). Связь длин волн исходного (λ) и рассеянного фотона (λ′) определяется формулой Комптона
λ′−λ = λC (1−cosθ) ,
где λC |
– комптоновская |
длина волны электрона с массой m, |
|
λC = 2π |
/ mc. Найдем отсюда отношение |
||
|
λ′ |
=1+(1−cos θ) λC |
|
|
λ |
λ |
|
и подставим это в (1) |
|
|
|
|
tg ϕ = |
sin θ |
|
|
|
. |
|
|
(1−cosθ)(1+λC / λ) |
||
С учетом того, что λC / λ = |
ω/ mc2 , после упрощений находим |
||
tg ϕ = 1+ ω/ mc2 .
Определим теперь, как угол ϕ зависит от импульса электронов p отдачи и энергии налетающих фотонов ε = ω. Для этого обратимся к закону сохранения энергии
ε+mc2 = ε′+c p2 + m2c2
179
(ε′ – энергия рассеянных фотонов). Из данного равенства нетрудно
найти |
|
(ε−ε′)(ε−ε′+ 2mc2 ) = p2c2 . |
(1) |
Кроме того, из рис. 3.10 следует |
|
ε′2 = p2c2 +ε2 −2 pccosϕ |
(2) |
(мы учли, что k = ε/ c, k′ = ε′/ c). Из (1) и (2) находим |
|
(ε−ε′)(ε+ mc2 ) = pcεcosϕ . |
|
Так как разность энергий фотона равна кинетической энергии электрона отдачи Ek , то
cos ϕ = Epck 1+ mcε 2 .
И вспомнив, что |
Ek |
= c |
p2 +m2c2 −mc2 , |
получаем оконча- |
|||||||
тельно |
|
|
|
|
|
|
|
|
|
|
|
|
p |
2 |
|
2 |
c |
2 |
−mc |
|
|
2 |
|
cos ϕ = |
|
+ m |
|
1 |
+ mc |
|
. |
||||
|
|
|
|
|
|
|
|
||||
|
|
|
|
p |
|
|
|
|
ω |
|
|
2. В результате столкновения фотона с покоившимся свободным электроном углы, под которыми рассеялся фотон и отлетел электрон отдачи, оказались одинаковыми и угол между направлениями их разлета 2α = = 100°. Найти длину волны налетевшего
фотона.
Так как углы, под которыми рассеялся фотон и отлетел электрон отдачи, одинаковы, то закон сохранения импульса в проекциях на оси х, у (рис. 3.11) примет
Рис. 3.11 вид
180
