random books / Паршаков А.Н. - Принципы и практика решения задач по общей физике. Часть 3_ Оптика. Квантовая физика

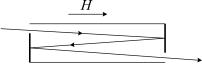
Оптически активное вещество является правовращающим, если вращение плоскости поляризации света происходит по часовой стрелке, если смотреть навстречу лучу. Термин положительное ве-

щество означает, что вращение плоскости поляризации в продольном магнитном поле составляет правый винт относительно вектора H.

Внашей задаче, если смотреть навстречу вышедшему свету

иположительное направление угла отсчитывать по часовой стрелке, естественное вращение дает положительный угол поворота ϕ = αl

(при обратном движении луча угол меняет знак). Магнитное же вращение дает отрицательный угол поворота (смотрим против векто-

ра H ). Этот угол не зависит от направления луча и суммируется при каждом его отражении, поэтому ϕ = −VlHN. В итоге угол поворота составит

ϕ = αl −VlHN = l (α−VHN ) ,

где N – число отражений.

151

Глава 3 КВАНТОВАЯ ОПТИКА

Квантовая природа излучения заключается в том, что излучение и поглощение света веществом происходит не непрерывно, а конечным порциями – квантами. Кроме того, и распространение света в пространстве происходит отдельными порциями, причем энергия каждой такой порции определяется формулой Планка ε = ω ( –

постоянная Планка). Эти порции (частицы) называют квантами света или фотонами. Как и для обычного электромагнитного излучения

кфотонам применимо понятие поляризации. Своеобразие формулы

ε= ω проявляется в том, что по классическим (волновым) пред-

ставлениям энергия должна быть связана не с частотой ω, а с амплитудой колебаний. В актах взаимодействия с веществом (но не между собой) фотоны могут поглощаться, испускаться и рассеиваться. При этом выполняются законы сохранения энергии и импульса. В то же время в отличие от обычных частиц для фотонов не существует закона сохранения числа частиц.

3.1. Тепловое излучение

Тепловое излучение за счет внутренней энергии тел является единственным видом излучения, которое может находиться в равновесии с излучающими телами.

Интенсивность теплового излучения характеризуется величиной плотности потока энергии – энергетической светимостью R (Вт/м2),

R = ∆∆SW∆t = ∆Φ∆t ,

где ∆W – энергия, испускаемая с поверхности ∆S за время ∆t по всем направлениям; ∆Φ – поток энергии, ∆Φ = ∆W / ∆t.

Для характеристики излучения (отражения) света в заданном направлении существует понятие яркости L,

152

L = dΦ , dΩ∆S cos θ

где dΦ – поток энергии, излучаемой площадкой ∆S, в пределах телесного угла dΩ в направлении полярного угла θ относительно нормали к площадке ∆S. Единицей яркости служит кандела на квадратный метр (кд/м2). Источники, яркость которых одинакова по всем направлениям, – ламбертовские. Для них R = πL.

Самыми простыми закономерностями спектрального состава обладает излучение так называемого абсолютно черного тела, которое по определению полностью поглощает падающее на него излучение всех частот при любых температурах T. В дальнейшем все энергетические величины, относящиеся к излучению абсолютно черного тела, будем снабжать символом (*).

Спектральное распределение энергии характеризуют спек-

тральной плотностью энергетической светимости (испускательная способность) rω

rω = dRdωω ,

где dRω – поток энергии, испускаемой единицей поверхности в интервале частот (ω, ω+dω). Соответственно, полная энергия по всем частотам

∞

R = ∫ rωdω.

0

Спектральную плотность энергетической светимости r можно выражать и как функцию длины волны λ, выбирая интервалы dω и dλ такими, чтобы в них находилась одинаковая энергия:

rωdω= rλdλ → rλ = 2λπ2c rω ,

где c – скорость света в вакууме.

153

Спектральная плотность энергетической светимости абсолютно черного тела rω связана со спектральным распределением объемной плотности энергии теплового излучения w(ω,T ) (Дж·с/м3) соотно-

шением

rω = 4c w(ω,T ) ,

где

w(ω,T ) = dWdωω ,

dWω – объемная плотность энергии в пространстве, приходящейся на интервал частот (ω, ω+ dω) при заданной температуре T.

Величину w(ω,T ) можно рассматривать как функцию распре-

деления при расчете среднего значения любой функции частоты

ϕ(ω):

154

Данная формула приводит к «ультрафиолетовой катастрофе», согласно которой абсолютно черное тело должно мгновенно испустить всю свою энергию в виде импульса коротковолнового электромагнитного излучения. Причина этого заключается в предположении равномерного распределения энергии по степеням свободы.

Правильное выражение для rω получено Планком в предполо-

жении, что электромагнитное излучение должно испускаться порциями энергии ε = ω. Тогда для средней энергии, приходящейся на одно электромагнитное колебание, получается

Из последней формулы сразу следуют законы теплового излучения абсолютно черного тела:

155

не являющихся абсолютно черными, закон Стефана–Больцмана записывают в виде R = ησT 4 , где 0 < η<1 – степень черноты.

3.1.1. Три плоскости. Посередине двух параллельных плоскостей с температурами T1 и T2 находится третья плоскость. Какова ее

температура, если все три плоскости абсолютно черные?

Каждая плоскость является не только источником излучения, но и его приемником. Причем, так как плоскости являются абсолютно черными, они поглощают всю падающую на них энергию. Неизменность температуры средней плоскости обеспечивается равенством плотностей потоков энергии, поступающих от крайних пластин, и ее собственного потока излучения:

σT14 +σT24 = 2σT 4

(множитель 2 справа введен из-за того, что средняя пластина излучает в обе стороны). Откуда находим

3.1.2. Поток тепла между двух плоскостей. Определить плот-

ность теплового потока, передаваемого от одной параллельной пластины к другой, если температура пластин T1 и T2 , а степень черно-

ты – соответственно η1 и η2. Площадь каждой пластины S, зазор

между пластинами много меньше их размеров.

Если мы сейчас определим плотность потока тепла, передаваемого от одной пластины к другой, как разность плотности потока излучения каждой из пластин, то мы совершим ошибку. В отличие от предыдущей задачи в потоке излучения, идущего от каждой пластины, присутствует как ее собственное излучение, так и отраженное излучение, формирующееся от соседней пластины. Связано это с тем, что пластины не являются абсолютно черными. Собственный

поток излучения каждой из пластин равен соответственно η1σT14 и η2σT24. Значительно сложнее дело обстоит с отраженными потока-

156

ми, так как происходит их многократное отражение. Обратимся, например, к первой пластине и будем полагать, что ее излучение было включено в некоторый момент времени. Вначале появится плотность

потока η1σT14. Затем это излучение отражается от второй пластины с коэффициентом отражения 1−η2 , попадает на первую пластину, отражается от нее с коэффициентом отражения 1−η1 и т.д. Таким

образом, плотность потока излучения, идущего от первой пластины и сформированного данной пластиной, определится как

ΦS12′ = η1σT14 +η1σT14 (1−η2 )(1−η1 ) +η1σT14 (1−η2 )2 (1−η1 )2 +... =

Но мы забыли, что от первой пластины отражается и излучение, сформированное второй пластиной. Нетрудно сообразить, что его можно найти как

ΦS12′′ = η2σT24 (1−η1 ) +η2σT24 (1−η1 )2 (1−η2 ) +

Выражения, стоящие в квадратных скобках (1) и (2), являются суммой сходящейся геометрической прогрессии со знаменателем

157

Совершенно аналогично находим полный поток, идущий от второй пластины к первой (для этого нужно просто заменить индекс 1 на 2 и наоборот):

И в итоге, вычитая выражения (3) и (4), получаем

Φ = ση1η2 (T14 −T24 ) .

S η1 +η2 −η1η2

3.1.3. Две полости с отверстиями. Имеются две полости 1 и 2

с малыми отверстиями одинакового радиуса r = 5,0 мм и абсолютно отражающими наружными поверхностями. Полости отверстиями обращены друг к другу, причем расстояние между отверстиями l =

= 100,0 мм (рис. 3.2). В полости 1

поддерживают температуру T1 =

=1250 K. Найти установившуюся

температуру в полости 2. Считать, что абсолютно черное тело являет-

Рис. 3.2 ся ламбертовским излучателем. Условием теплового равновесия в данном случае является

равенство потоков энергии, выходящей из полости 2 и проникающей в нее. Из полости 2 выходит поток энергии R 2∆S = σT24∆S (∆S = πr2 – площадь отверстия). Для расчета потока энергии, прони-

кающей в отверстие второй полости из первой, воспользуемся понятием яркости. Эта величина как раз и вводится для определения потока энергии в заданном направлении. Пусть яркость отверстия 1 равна L1. Тогда в направлении отверстия 2 по определению яркости

идет поток энергии L1∆Ω∆S, где ∆Ω = ∆S / l2 (полагаем, что оси от-

верстий 1 и 2 совпадают). Кроме того, так как по условию задачи отверстия являются ламбертовскими излучателями (их яркость не зави-

158

сит от направления), то L1 = R1*/π = σT14/π. Таким образом, условие теплового равновесия принимает вид

3.1.4. Медный шарик. Медный шарик радиусом r = 10,0 мм с абсолютно черной поверхностью поместили в откачанный сосуд, температура стенок которого поддерживается близкой к абсолютному нулю. Начальная температура шарика T0 = 300 K. Через какое

время его температура уменьшится в η = 1,5 раза? Удельная теплоемкость меди c = 380 Дж/(кг К), ее плотность ρ =8,9 103 кг/м3.

Будем полагать, что температура шарика за счет излучения падает достаточно медленно и успевает выровняться по объему шарика (иначе нам придется решать дифференциальное уравнение теплопроводности с заданными граничными и начальными условиями). Составим для этого случая уравнение теплового баланса:

δQ = cmdT ,

где m – масса шарика, m =ρ43 πr3; dT – малое изменение темпера-

туры за время dt за счет излучения. Значение излучаемого тепла δQ при температуре шарика в данный момент времени равно произведению энергетической светимости σT 4 на площадь поверхности шарика 4πr2 и dt:

δQ = −σT 4 4πr2dt

159

(знак минус поставлен из-за того, что тепло уходит от шарика). Таким образом, приходим к дифференциальному уравнению

−cmdT = 4πr2T 4dt.

Интегрируя данное уравнение с учетом начального условия T =T0 , получаем

Откуда находим

t = cρr η3 −3 1, 9σ T0

что после подстановки численных значений составит t = 1,6 ч.

3.1.5. Теплоемкость полости. Полость объемом V =1 л заполнена тепловым излучением при температуре T =1000 К. Какова ее теплоемкость Cv ?

Из термодинамики известно, теплоемкость при постоянном объеме равна производной по температуре от внутренней энергии системы при постоянном объеме:

C= ∂U .

v∂T V

Внашем случае внутренняя энергия U равна энергии теплового излучения внутри полости, которую можно представить как произведение объемной плотности энергии W на объем полости V. В свою очередь объемная плотность энергии излучения связана с энергети-

ческой светимостью стенок полости R соотношением W = 4R / c. В итоге для U имеем

U = 4c R V = 4c σT 4V.

160