
random books / Парамонов - Физика. Оптика.2. Волновая оптика_ учебное пособие
.pdf
2. Плоская монохроматическая волна бежит в направлении оси z1 , составляющей угол β с осью z . Какова разность фаз ко-
лебаний в двух точках любой плоскости z = const , расстояние между которыми равно x ?
Решение:
На рис. 27 изображена плоскость z = const (перпендикулярная оси z ) и две волновые поверхности: AA' , в которой лежит точка О, и BB' , в которой находится точка Р ( OP = x ). Расстояние между поверхностями OD = ∆z1 .
A B x |
|
P |
z |
|
|
O D |
z |
A |
B |
∆z1 |
Рис. 27
Пусть колебания на волновой поверхности AA' (и в точке О этой поверхности) происходят по закону
E(t)= acosωt .
Тогда на поверхности BB' (и в частности, в точках D и P) колебания отстают по азе на величину
∆ϕ = k∆z1 = k OP sin β = kxsin β .
Таким образом, разность фаз колебаний в двух точках плоскости z = const зависит от расстояния между точками по линейному закону
∆ϕ(x)= (k sin β)x .
Линейный закон изменения фазы колебания по некоторой плоскости z = const означает, что имеется плоская волна, направление распространения которой составляет угол β с осью z , перпендикулярной этой плоскости.
41
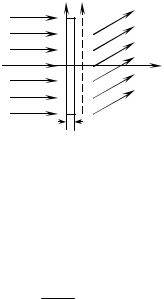
3. Плоская световая волна (длина волны λ0 ) падает нор-
мально на тонкую прозрачную пластинку толщиной d (рис.28). Показатель преломления пластинки меняется вдоль координаты x
|
|
|
x |
|
|
по закону |
n(x)= n 1 |
+ |
|
|
. Найдите распределение фазы колеба- |
|
|||||
ний ϕ(x) |
|
|
b |
|
|
на выходе из пластинки. В каком направлении будет |
|||||
распространятся волна за пластинкой?
x x
 z
z
d
Рис. 28
Решение:
Пусть в плоскости, примыкающей к пластинке слева, падающая волна создает колебания
E0 = acosωt .
Время распространения волны через пластинку в разных местах различно и равно
τ (x)= υ(dx) = dc n(x).
Тогда на выходе из пластинки (в плоскости, примыкающей к ней справа) получаем
E(t)= acosω(t −τ )= acos ωt −ω n(x)d ,
c
или
E(t)= acos(ωt −k0n(x)d ),
42
где k0 = ωt – волновое число в вакууме.
Распределение фазы колебаний на выходе из пластинки есть
ϕ(x)= k0dn(x). |
|
|||
|
|
x |
|
|
Подставляя функцию n(x)= n 1 |
+ |
|
|
, находим |
|
||||
|
|
b |
|
|
ϕ(x)=ϕ0 +k0n0 db x ,
где ϕ0 = k0n0d – константа. Мы получили линейный закон изме-
нения фазы колебаний в плоскости, примыкающей к пластинке справа. Это означает, что, пройдя через пластинку, волновой фронт повернулся (как показано на рисунке) на угол
β = arcsin nb0d .
Направление распространения составляет угол β с осью z – таким образом пластинка эквивалентна призме.
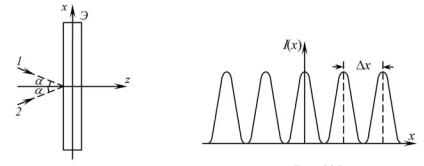
4. Две монохроматические волны одинаковой амплитуды (долина волны λ ) падают на плоский экран, как показано на ри- с.29а. Угол между сходящимися пучками света равен 2α . Найдите распределение интенсивности света на экране и ширину интерференционных полос, т.е. расстояние между двумя соседними светлыми полосами.
Рис. 29а |
Рис. 29б |
43
Решение:
Воспользуемся результатами задачи 2. Распределение фазы колебаний, создаваемых волной 1 на экране, запишем в виде
ϕ1 = kxsinα , а волной 2 – в виде ϕ2 = −kxsinα .
Тогда разность фаз колебания равна ∆ϕ = 2kxsinα , а интенсивность – I = 2I0 (1+cos(2kxsinα)).
График функции I = I (x) изображен на рис.29б.
Максимальной интенсивности соответствует условие cos(2kxsinα) =1,
откуда 2kxsinα = 2πm и xmax = kπsinmα .
При этом ширина интерференционной полосы равна
∆x = 2sinλ α .
Для малых углов схождения 2α можно записать
∆x = 2λa .
5. Интерферируют две синфазные плоские волны. Чему равна ширина x интерференционной полосы, если угол схождения волн на экране α , а длина волны λ ?
Решение:
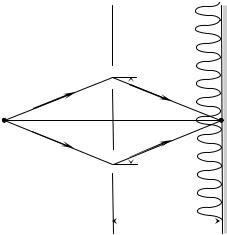
На рис.30 изображены положения волновых фронтов в некоторый момент времени.
Сплошные линии соединяют точки, где в этот момент напряженность электрического поля принимает амплитудное значение E = +A. Расстояние между соседними сплошными линиями равны. Штриховые линии соединяют точки, где напряженность поля
E= −A. Расстояниемеждуштриховымилиниямитожеравны.
Вточках O, M, N, M*, N* и т.д. две волны встречаются в одинаковых фазах. Поскольку фазы колебаний обеих волн одинаково
меняются со временем (ϕ =ωt +ϕ0 ), то в любой момент времени
волны будут приходить в эти точки в одинаковых фазах и, следовательно, усиливать друг друга. Точки O, M, N, M*, N* соответствуют интерференционным максимумам.
44

|
|
|
|
|
N* |
|
|
|
|
|
|
|
|
|
M* |
|
|
|
|
d |
|
α |
|
|
O |
|
|
|
|
|
|
L |
|
|
M |
|
x |
||
|
|
|
|
|
|
2x |
|||
|
|
C |
|
|
|
||||
|
|
|
N |
|
|
||||
|
|
|
|
|
|
||||
|
|
|
|
λ |
|
|
|
||
|
|
|
|
|
|
|
|
||
|
|
|
Рис. 30 |
|
|
|
|
||
Из рис.30 видно, что NOC = |
α , NO = 2x , CN = λ . |
||||||||
|
λ |
|
α |
≈ α |
2 |
λ |
|
|
|
Изсоотношения |
= sin |
найдем x = |
|
(длямалых α ). |
|||||
2x |
2 |
α |
|||||||
|
|
2 |
|
|
|
||||
Таким образом, ширина интерференционной полосы зависит от длины волны источников и угла схождения.
Этот результат справедлив для любой интерференционной схемы с малым углом схождения и углом схождения лучей (при достаточном удалении от источников волны всегда можно считать
плоскими). В частности, для точечных источников α = dL ;
x = αλ = λdL .
В красном свете ( λ ≈ 7 10−7 м) полосы шире, чем в зеленом ( λ = 5,5 10−7 м); с удалением экрана от источников полосы расширяются ( x L); сближение источников также ведет к расшире-
|
1 |
||
нию полос x |
|
. |
|
d |
|||
|
|
||
45
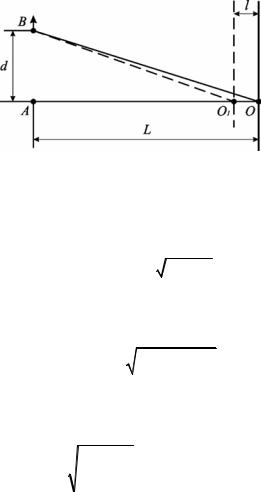
6. От точечного монохромного источника А (рис.31) отодвигают точечный монохромный источник В (источники когерентны и синфазны) до тех пор, пока в точке О, где наблюдается интерференция, не наступает потемнение. Расстояние между А и В при этом равно d = 2 мм. Расстояние между источником А и экраном составляет L = 9 м. На сколько нужно придвинуть экран к источнику А, чтобы в центреэкрана (точке О1) снова возникло потемнение?
Рис. 31
Решение:
При удалении источника В первое потемнение в точке О возникает при условии, что разность хода волн от В и А равна половине длины волны.
∆r = BO − AO = λ |
, или |
L2 +d2 − L = λ . |
|
1 |
2 |
|
2 |
|
|
||
Если экран приблизить к источникам на расстояние l, минимум в точке О будет соответствовать разности хода три вторых длины волны:
∆r1 = BO1 − AO1 = |
3λ |
, или |
(L −l)2 +d2 |
−(L −l)= |
3λ |
. |
||||||
2 |
2 |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|||
Преобразуем полученные выражения и воспользуемся при- |
||||||||||||
|
1 |
|
|
x |
|
|
|
|
|
|
||
ближенной формулой (1+ x)2 |
=1 |
+ |
для x |
1: |
|
|
||||||
|
|
|
||||||||||
|
|
|
|
2 |
|
|
|
|
|
|
||
|
|
d 2 |
|
|
|
λ |
|
|
|
|
||
|
1+ |
|
−1 = |
|
; |
|
|
|
||||
|
2L |
|
|
|
||||||||
|
|
L |
|
|
|
|
|
|
|
|||
|
|
|
46 |
|
|
|
|
|
|
|
||
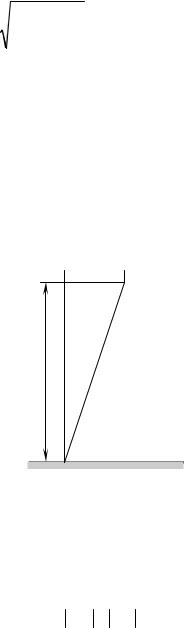
|
d 2 |
|
3λ |
|
||
1+ |
|
|
−1 |
= |
|
, |
|
2(L −l) |
|||||
|
L −l |
|
|
|
||
или
d2 = λL ,
d2 = 3λ(L −l).
Отсюда l = 23 L = 6 м.
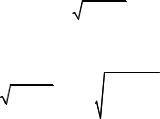
7. Два когерентных источника S1 и S2 (рис.32) с длиной
волны 0,5 мкм находится на расстоянии 2 мм друг от друга. Параллельно линии, соединяющей источники, расположен на экране на расстоянии 2 м от них. Что будет наблюдаться в точке А экрана?
d
S1 S2
S2

 ∆
∆
l
A
Рис. 32
Решение:
В точке А экрана будет максимум интенсивности, если разность хода двух лучей, исходящих из источников S1 и S2 ,
равна целому числу длин волн, и минимум интенсивности, если эта разность хода равна нечетному числу полуволн. Вычислим разность хода:
∆ = S2 A − S1 A ,
47
где
|
|
|
|
|
S2 A |
|
= |
|
|
|
l2 +d2 |
, |
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
||||||||||||
Следовательно, |
|
|
|
|
|
|
S1 A |
|
= l . |
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
∆ = |
l |
2 |
+d |
2 |
|
−l |
= l 1+ |
d 2 |
−l . |
|||||||||||
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
l |
|
|
|
Так как d |
1, то, |
используя формулу приближенного вы- |
|||||||||||||||||||
l |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
числения, получаем |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
d 2 |
|
|
d |
2 |
|
||||||||
|
∆ ≈ l 1+ |
|
|
|
|
|
|
|
|
−l = |
|
|
; |
||||||||
|
2 |
|
|
|
|
2l |
|||||||||||||||
|
|
|
|
|
|
|
|
l |
|
|
|
|
|||||||||
|
|
|
|
|
(2 10−3 )2 |
|
|
|
|
|
|
||||||||||
|
|
∆ ≈ |
=10−6 м. |
|
|||||||||||||||||
|
|
|
|
|
|
|
|
2 2 |
|
|
|
|
|
|
|
|
|
|
|||
8. Сначала вертикальную мыльную пленку наблюдают в отраженном свете через красное стекло ( λ = 6,3 10−7 м). При этом расстояние между соседними красными полосами равно 3 мм. За-
тем эту пеленку наблюдают через синее стекло ( λ = 4 10−7 м). Найти расстояние между соседними синими полосами. Считать, что форма пленки за время наблюдения не изменяется.
Решение:
В глаз наблюдателя попадают лучи, отраженные от тонкого клина перпендикулярного его поверхности. Тогда для k-й и ( k +1 )-й красных полос оптические разности хода (рис.33а) соответственно равны
∆k = 2hkn − λ21 = kλ1 ,
∆k+1 = 2hk+1n − λ21 = (k +1)λ1
( cos r =1 в обоих случаях). Здесь hk и hk+1 – соответствующие
данным полосам толщины вертикальной мыльной пленки, сечение которой – клин.
48
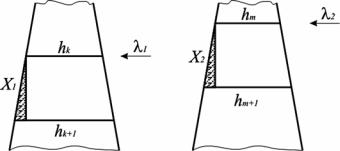
Рис. 33а Рис. 33б
Из соотношений
∆k = 2hkn − λ21 = kλ1 ,
∆k+1 = 2hk+1n − λ21 = (k +1)λ1
находим
∆k+1 −∆k = 2hk+1n − λ21 − 2hk n − λ21 = (k +1)λ1 −kλ1 ,
откуда
2n(hk+1 −hk )= λ1 .
Аналогично для синих полос (рис.33б)
2n(hm+1 −hm )= λ2 .
Разделив почленно выражения
2n(hk+1 −hk )= λ1 и 2n(hm+1 −hm )= λ2 ,
получим
hk+1 −hk |
= |
λ1 |
. |
|
|
|
|||
h |
−h |
|
λ |
|
m+1 |
m |
|
2 |
|
Из подобия заштрихованных треугольников следует
hk+1 −hk |
= |
x1 |
. |
|
|
|
|||
h |
−h |
|
x |
|
m+1 |
m |
|
2 |
|
|
49 |
|
|
|
Приравнивая правые части выражений |
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
hk+1 −hk |
= |
|
λ1 |
|
и |
hk+1 −hk |
= |
|
x1 |
|
, |
||||
|
|
|
|
|
|
|
λ |
|
|
|
x |
|
|||||||||
|
|
|
|
|
|
h |
−h |
|
|
|
|
h |
|
−h |
|
|
|
|
|||
|
λ1 |
|
x1 |
|
|
m+1 |
m |
|
2 |
|
|
m+1 |
m |
|
2 |
|
|
||||
находим |
= |
|
|
, откуда |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
λ |
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
2 |
2 |
|
|
|
|
|
|
|
|
|
λ2 |
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
x |
= x |
; |
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
2 |
|
1 λ |
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
x = 3 10−3 |
|
4 10−7 |
|
=1,9 10−3 |
м. |
||||||||||||
|
|
|
|
6,3 10−7 |
|||||||||||||||||
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
||||||||
9. |
Точечный |
монохроматический |
|
источник света S |
|||||||||||||||||
( λ = 5 10−5 см) освещает непрозрачный экран с двумя маленькими отверстиями S1 и S2 (рис.34), расстояние между которыми
d =1 см. Интерференционная картина возникает в плоскости наблюдения Э, находящейся от экрана с отверстиями на расстоянии h = 2 м. Определите ширину интервенционной полоски.
Э
S1
S |
d |
P |
|
S2
h
Рис. 34
50
