
random books / Летута, С. Н. - Курс физики. Оптика (2014)
.pdf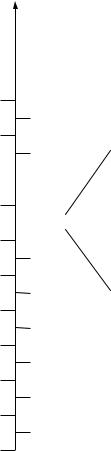
|
|
|
|
|
|
|
|
|
|
|
|
|
Уравнения |
Максвелла. |
|
Частота в |
Длина волны |
Система уравнений |
для |
электро- |
|||||||||||
герцах |
|
|
в сантиметрах |
магнитного поля была |
выведена |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
||||
Рентгенов- |
|
|
|
|
|
|
|
|
10-8 |
|
|
Максвеллом (см., например, Чакак |
|||
ские лучи |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1018 |
|
10-7 |
|
|
А.А., Курс физики. Электричество |
|||||||||
|
|
|
|
|
|
|
|
||||||||
|
1017 |
|
|
|
|||||||||||
|
|
10-6 |
|
Фиолетовый |
и магнетизм, Оренбург: ГОУ ОГУ, |
||||||||||
|
1016 |
|
|
||||||||||||
|
|
|
|
10-5 |
|
Синий |
2009. – 317 с., § 8.42) в середине |
||||||||
|
|
|
|
||||||||||||
Видимый 10 |
15 |
|
|
|
|
Голубой |
XIX в. путём обобщения данных, |
||||||||
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
Зелёный |
|||||||
|
|
|
|
|
|
|
|||||||||
свет |
1014 |
|
|
|
|
|
|
|
Жёлтый |
полученных в опытах с электриче- |
|||||
|
10-3 |
||||||||||||||
|
1013 |
|
|
Оранжевый |
скими зарядами, токами и магни- |
||||||||||
|
|
|
|
|
|
|
|
||||||||
|
1012 |
|
10-2 |
|
Красный |
тами. Дальнейшие |
исследования |
||||||||
|
|
|
|||||||||||||
|
|
10-1 |
|
|
|||||||||||
|
10 |
11 |
|
|
|
показали, что уравнения Максвел- |
|||||||||
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
100 |
|
|
|
|
|
|
||||||
|
1010 |
|
|
|
|
ла имеют очень глубокое физиче- |
|||||||||
|
|
101 |
|
|
|
||||||||||
Радио- |
109 |
|
|
|
|
ское содержание, далеко выходя- |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
102 |
|
|
|
щее за рамки тех фактов и пред- |
||||||||
волны |
108 |
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||
Рисунок 17 |
ставлений, на основе которых бы- |
|
ли получены уравнения. Оказа- |
||
|
лось, что эти уравнения удовлетворяют условию релятивистской инвариантности, хорошо описывают быстропеременное электромагнитное поле, включая световые волны, могут быть положены в основу теории излучения электромагнитных волн движущимися зарядами и теории взаимодействия света и вещества.
Электромагнитная волна характеризуется колебанием двух векторов: вектора напряжённости электрического поля Е и вектора магнитной индукции В. Оба вектора в плоской волне изменяются во взаимно перпендикулярных плоскостях в одинаковой фазе, т.е. одновременно достигают максимальных и нулевых значений. Скорость распространения волны v перпендикулярна к направлениям обоих векторов Е и В.
На рисунке 18 колебания вектора Е, изображённые сплошной линией, происходят в плоскости x0z, колебания вектора В, изображённые пунктирной
51
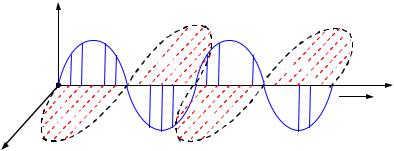
линией, происходят в плоскости y0z, волна распространяется в направлении положительной оси 0z.
Электромагнитная теория света показывает, что при отражении лучей под углом Брюстера в отражённом луче вектор напряжённости электрического поля Е колеблется в плоскости, перпендикулярной плоскости падения; вектор магнитной индукции В колеблется в плоскости падения. В § 1.7 было указано, что луч, отражённый под углом Брюстера, условно считается поляризованным в плоскости падения. Таким образом, оказывается, что в поляризованной волне
вектор напряжённости элек- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
трического поля Е колеб- |
|
|
|
|
x |
Е |
|||||||||||||||
|
|
|
|
|
|
||||||||||||||||
лется в плоскости, перпен- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
z |
||
дикулярной к плоскости по- |
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ляризации; вектор магнит- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
v |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
ной индукции В колеблется |
|
|
В |
|
|
|
|
|
|
Рисунок 18 |
|
||||||||||
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|||||||||||||||
в плоскости поляризации. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Из опытов было установлено, что фотохимическое действие света в фотографическом слое вызывается колебаниями вектор напряжённости электрического поля Е; то же относится и к другим действиям света – люминесценции, фотоэффекту и физиологическим действиям. По этой причине вектор Е часто называют «световым вектором».
Вектор напряжённости электрического поля Е и вектор магнитной индукции В на границе раздела двух веществ подчиняются различным пограничным условиям. Это ведёт к тому, что при образовании стоячих волн в результате отражения от металлического зеркала пучности вектора напряжённости электрического поля совпадают с узлами вектора магнитной индукции и наоборот. На поверхности зеркала вектор Е имеет узел (это означает, что при отражении све-
та от зеркала фаза волны Е изменяется на π), а вектор В – пучность.
Опыты со стоячими волнами, получаемыми в поляризованном свете, позволяют непосредственно проверить, что вектор Е в световой волне колеблется перпендикулярно к плоскости поляризации. Эти опыты заключаются в сле-
52
дующем: свет, поляризованный в плоскости падения, отражается под углом 450 от металлической зеркальной поверхности. Так как вектор Е в данном случае колеблется в плоскости, перпендикулярной к плоскости падения, то в падающей и отражённой волнах колебания вектора напряжённости электрического поля Е происходят параллельно друг другу. Поэтому они интерферируют и образуют стоячие волны, которые в действительности и наблюдаются. Если бы вектор Е колебался в плоскости поляризации, то направления колебаний в падающей и отражённой волнах в данном случае были бы взаимно перпендику-
лярны и интерференция не имела бы места, − стоячие волны не возникли бы. Длины волн, испускаемых атомами и молекулами, не ограничиваются ин-
тервалом от 0,7 мкм до 0,4 мкм, в пределах которого волны способны действовать на наш глаз и вызывать субъективное зрительное ощущение. Раскалённые тела, газы, светящиеся под влиянием электрического разряда, и другие источники света одновременно испускают волны длин и больших чем 0,7 мкм и меньших чем 0,4 мкм. Также современные методы возбуждения (генерирования) электромагнитных волн с помощью макроскопических вибраторов позволяют получить волны с длинами, лежащими в весьма большом диапазоне. Наконец, существуют методы возбуждения электромагнитных волн, значительно более коротких, чем световые.
§ 1.9 Плотность потока энергии и импульса электромагнитных волн. Давление света
Световые волны переносят энергию, которую они берут от источника света, и отдают тому телу, которое их поглощает. Потоком световой энергии через какую-либо площадку называется количество энергии, переносимое светом через эту площадку за единицу времени. Таким образом, поток энергии имеет размерность мощности и может измеряться в джоулях в секунду, в ваттах и т.д. Измерение потока световой энергии в абсолютной мере схематически может быть проведено следующим образом. Световая энергия через отверстие S (ри-
53
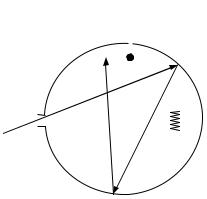
сунок 19) попадает внутрь почти замкнутого сосуда А с поглощающими стенками. При малых размерах отверстия S свет поглощается внутри сосуда А практически весь, независимо от длины волны, так как обратно из отверстия S выйдет лишь ничтожная его часть. В результате поглощения световой энергии стенки сосуда начнут нагреваться. При постоянных условиях теплоотдачи, в конце концов, установится термическое равновесие. Этому равновесию будет соответствовать определённая температура Т, которая измеряется термометром а. После того как температура Т измерена, доступ световой энергии в сосуд А прекращается и при тех же условиях теплоотдачи сосуд подогревается электрическим током, протекающим по спирали С. Сила тока подбирается такая, чтобы
температура Т осталась прежней. Очевидно, это |
|
|
|
|
|
|
|
|
|
|
произойдёт при условии, что мощность, разви- |
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
||
ваемая в спирали электрическим током, равна |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
мощности светового потока. Так как мощность |
S |
|
|
|
||||||
электрического тока может быть измерена в аб- |
|
|
|
|||||||
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
C |
|
|
|||
солютной мере по силе тока и сопротивлению |
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
проводника, то и поток световой энергии, таким |
|
|
|
|
|
|
A |
|||
Рисунок 19 |
|
|
|
|
||||||
образом, окажется измеренным в абсолютной |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
мере. |
|
|
|
|
|
|
|
|
|
|
Человеческий глаз способен воспринимать чрезвычайно малые мощности. При условии максимальной чувствительности глаза достаточно падения на площадь зрачка потока мощностью 2×10-16 Вт, чтобы возникло зрительное ощущение. Описанный способ измерения мощности света по нагреву гораздо менее чувствителен и позволяет измерять лишь значительно более мощные потоки. Существуют другие более чувствительные методы объективной регистрации и измерения светового потока, но преимущество описанного теплового метода заключается в возможности абсолютных измерений и в его одинаковой пригодности для света любой длины волны.
Электромагнитная теория света показывает, что свет оказывает давление на поверхность, которая его отражает или поглощает. К этому же выводу мож-
54
но прийти, учитывая, что световой поток обладает не только энергией, но и импульсом.
Плотность потока энергии − физическая величина, численно равная потоку энергии через единичную площадку, перпендикулярную направлению потока. Часто вводят также вектор плотности потока энергии (так называемый вектор Умова), величина которого равна плотности потока энергии, а направление совпадает с направлением потока. В электродинамике вектор плотности потока энергии электромагнитного поля носит название вектора Пойнтинга:
S = Е´Н, |
(9.1) |
модуль которого в случае плоской волны может быть представлен в виде
S = úSç = úЕ´Нç = úЕç×úНç= ЕВ/μ0 = (1/μ0с)Е2, |
(9.2) |
где Е – напряжённость электрического поля, Н – напряжённость магнитного поля, В – магнитная индукция, μ0 – магнитная постоянная,
с– скорость света в вакууме.
В(9.2) учтено следующее соотношение между напряжённостью электрического поля и магнитной индукцией плоской волны в вакууме
Е = сВ. |
(9.3) |
Принимая во внимание, что 1/μ0 = ε0с2, запишем соотношение (9.2) в форме
S = сε0Е2, |
(9.4) |
где ε0 − электрическая постоянная. 55
В (9.1) - (9.4) входят мгновенные значения величин. Однако векторы электромагнитной волны светового диапазона колеблются с частотами порядка 1015 Гц, поэтому нельзя следить за изменением величин по времени. Можно наблюдать и измерять лишь средние значения величин по очень большому числу периодов колебаний. Поэтому от мгновенных величин необходимо перейти к средним.
Учитывая, что E = E0coswt, где Е0 - амплитуда напряжённости электрического поля волны, находим среднюю по времени плотность потока энергии:
|
|
= сe0Е02 |
|
= |
1 |
сe0Е02. |
(9.5) |
|
S |
cos2ωt |
|||||
|
|
|
|
|
2 |
|
|
Распределение плотности потока по сечению пучка. Обычно в экспе-
рименте используют пучки света конечного поперечного сечения, по которому плотность потока распределена неравномерно. Мощность потока энергии в пучке по определению равна:
Р = ò |
|
S |
|
× ds, |
(9.6) |
|
|
||||
σ |
|
|
|
|
|
где s - площадь поперечного сечения пучка, перпендикулярного направлению распространения света.
Поскольку поперечные размеры пучка бывают обычно порядка 1 мм - 1 см, т.е. r0 » 103 - 104 мкм, а длина волны l имеет порядок 1 мкм, заключаем, что l/r0 »
10-3 - 10-4. Следовательно, дифракционные эффекты (см. § 2.16) в пучках малы и для расчёта плотности энергии можно использовать формулы для плоских электромагнитных волн.
Гауссов пучок. Чаще всего пучок имеет круговое сечение, распределение плотности энергии по которому аксиально-симметричное и гауссово. Такой пучок называется гауссовым. Амплитуды плоских электромагнитных волн, составляющих пучок, распределены по закону
56
E0(r) = A0exp(-r2/(2r02)), |
(9.7) |
где А0 − постоянная, равная амплитуде волн в центре пучка (r = 0); r – расстояние от центра.
Средняя плотность потока энергии равна:
|
1 |
2 |
2 |
2 |
2 |
2 |
|
|
S = |
2 |
ε0А0 |
exp(-r /r0 |
|
) = S0exp(-r /r0 |
|
), |
(9.8) |
где S0 = ε0А02/2 – средняя плотность энергии в центре пучка.
Для упрощения написания черты над величинами здесь не выписываются. Мощность потока энергии в пучке в соответствии с (9.6) равна:
P = S |
∞ |
−r2 / r0 |
2 2πrdr = S |
πr 2. |
(9.9) |
0 |
òe |
|
0 |
0 |
|
|
0 |
|
|
|
|
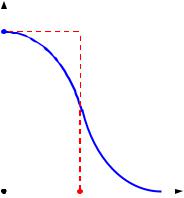
Фактически плотность энергии в гауссовом пучке распределена по экспоненциальному закону (9.8). На расстоянии r0 она убывает в е = 2,7 раза. По обычной договорённости об обращении с экспоненциально убывающими величинами можно сказать, что радиус пучка равен r0. В соответствии с (9.9) для оценочных расчётов полагают, что вся энергия пучка сосредоточена в пределах кругового сечения радиусом r0, а плотность по сечению постоянна и равна плотности в центре пучка. Гауссово распределение плотности потока и эффективное распределение показаны на рисунке 20 соответственно сплошной и штрихованной линией. Такой подход обычно обобщается и на другие, не гауссовы пучки. Мощность потока энергии пучка представляется в виде
P = Sэфπrэф2, |
(9.10) |
где Sэф – эффективная плотность потока энергии в пучке,
57
rэф – его эффективный радиус.
Если импульс света имеет энергию W, то его эффективная длительность τэф связана с мощностью потока энергии в импульсе соотношением
|
|
|
|
|
|
|
|
W = Pτэф. |
(9.11) |
|
|
S |
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
S0 |
|
|
|
|
|
|
В настоящее время с помощью лазеров по- |
||
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
лучены громадные плотности потока энергии, по- |
|
|
|
|
|
|
|
|
|
рядка S 1020 Вт/м2. Это означает (см. (9.4)), что |
|
|
|
|
|
|
|
|
|
напряжённости электрического поля в волне име- |
|
|
|
|
|
|
|
|
|
ют порядок Е ≈ 109 В/м, т.е. достигают значений, |
|
|
0 |
|
|
|
|
|
|
|
|
|
r0 |
|
|
r |
|
характерных для внутриатомных полей. Длитель- |
|||
|
|
|
|
|
|
||||
|
|
|
|
||||||
|
|
Рисунок 20 |
|
|
|
ность импульса τ = 10-12 с и менее. |
|||
|
|
Плотность |
импульса |
электромагнитной волны. |
Электромагнитная |
||||
волна обладает не только энергией, но и импульсом. Плотность импульса G электромагнитной волны связана с плотностью потока энергии S в ней соотно-
шением: |
|
G = S/c2. |
(9.12) |
Давление света. При поглощении или отражении света телом последнему по закону сохранения сообщается некоторый импульс, равный разности импульсов пучка света до и после поглощения или отражения. В результате на тело действует соответствующая сила и возникает световое давление. Идея о существовании давления света была высказана ещё Кеплером для объяснения отклонения хвостов комет от Солнца. Однако эта идея вызывала много споров, поскольку доказать существование светового давления долго не удавалось. Сторонники волновой теории долго считали, что световое давление не существует, а отсутствие экспериментального доказательства наличия светового давления выдвигали в качестве аргумента против корпускулярной теории, согласно которой световое давление, безусловно, должно существовать. Однако элек-
58
тромагнитная теория света предсказывает существование светового давления. Если электромагнитная волна падает нормально на плоскую поверхность твёрдого тела и полностью поглощается им, то в 1 с на 1 м2 поверхности тела в соответствии с (9.12) передаётся импульс G и, следовательно, световое давление равно:
P = cG = S/c. |
(9.13) |
При полном отражении поверхности тела передаётся импульс, в два раза больший, и, следовательно, в два раза больше давление. Можно подсчитать давление при частичном поглощении потока энергии. Если плотность потока поглощаемой энергии равна Sпог = aS, то по закону сохранения энергии плот-
ность потока отражаемой энергии Sотр = (1 - a)S и, следовательно, давление может быть представлено в виде P = aS/c + 2(1 - a)S/с = (2 - a)S/с. При падении потока энергии под углом к нормали необходимо принять во внимание лишь нормальную составляющую плотности потока энергии. Световое давление в обычных условиях очень мало. Например, на земной орбите плотность потока солнечного излучения составляет примерно S = 1400 Вт/м2, поэтому Р = 1400/(3×108) Па = 0,5×10-5 Па. Учитывая, что атмосферное давление составляет около 105 Па, находим, что световое давление Земли примерно 1010 раз меньше атмосферного. Поэтому обнаружить его было очень трудно. Первый шаг в правильном направлении сделал У. Крукс (1832-1919). Он использовал крутильные весы, лепестки которых облучались светом. По закручиванию нити можно было судить о действующей на лепестки силе. Однако из-за так называемого радиометрического эффекта, вызываемого нагреванием остатков газа у поверхности лепестков, ему не удалось измерить световое давление. Это впервые удалось сделать П.Н. Лебедеву (1886-1912) в 1900 г. Радиометрические силы были им уменьшены в результате создания глубокого вакуума в сосуде, в котором находились крутильные весы. Благодаря этому сила светового давления стала играть доминирующую роль в закручивании нити крутильных весов и была измерена.
59

Экспериментальная проверка достоверности исключения радиометрических сил состоит в следующем. Если поверхность, на которую направляется луч, отражающая, то давление света на нее в два раза больше, чем, если бы она была полностью поглощающей, а радиометрическое действие меньше. Если же поверхность полностью поглощает излучение, то световое давление на нее в два раза меньше, чем давление на полностью отражающую поверхность, а радиометрические силы – больше. П.Н. Лебедев действительно наблюдал этот эффект увеличения в два раза светового давления при освещении отражающего крылышка крутильных весов по сравнению с освещением поглощающего (чёрного) крылышка, что и доказывает исключение радиометрического действия.
Световое давление является проявлением объёмной плотности импульса у волны и закона сохранения импульса при взаимодействии волны с веществом.
Действие светового давления на малые частицы. Световое давление пропорционально площади, т.е. квадрату линейных размеров частицы, а масса частицы пропорциональна объёму, т.е. кубу линейных размеров. Это означает, что при фиксированной плотности сила, возникающая за счёт светового давления и приходящаяся на единицу массы, изменяется обратно пропорционально линейным размерам частицы, т.е. растёт с уменьшением ее размеров. Пусть,
например, у шарообразной частицы r = 103 кг/м3, r = 10-5 м. Масса частицы m = 43 pr3r = 4×10-12 кг. При потоке S = 1400 Вт/м2 солнечного излучения на орбите
Земли световое давления Р= S/c = 0,5 мкПа и поэтому сила, действующая на полностью поглощающую излучение частицу, F = Ppr2 = 1,5×10-15 Н. Она сооб-
щает частице ускорение a = F/m = 0,4×10-3 м/с2. Это большое ускорение. Ускорение, сообщаемое Солнцем частице на орбите Земли, равно аС = v2/R =
[(30×103)2/(15×1010)] м/с2 = 0,6×10-2 м/с2, т.е. примерно в (аС/а) » 15 раз больше ус-
корения вследствие светового давления. Для частицы с меньшими в 15 раз линейными размерами сила, обусловленная световым давлением, примерно уравновесит силу притяжения Солнца. Поскольку как плотность потока излучения, так и сила тяжести убывают с расстоянием по одному и тому же закону (обрат-
60
