
random books / Летута, С. Н. - Курс физики. Оптика (2014)
.pdf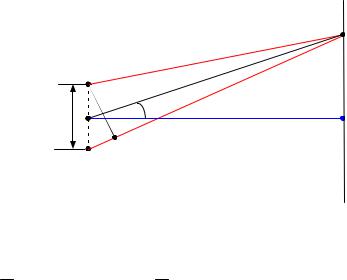
Пусть точечные источники волн S1 и S2 расположены друг от друга на расстоянии d (рисунок 12). Колебания в точках S1 и S2 совершаются в одной фазе. Пусть результат интерференции волн наблюдается на экране DD′, распо-
ложенном от точек S1 и S2 на расстоя- |
|
|
|
|
|
|
|
|
|
D |
нии L, большом по сравнению с d. Оп- |
|
|
|
|
|
|
|
|
|
Р |
|
|
|
|
|
|
|
|
|
|
|
ределим разность хода , с которой |
|
S1 |
|
ℓ |
||||||
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
приходят волны в точку экрана Р, от- d |
|
|
|
|
|
|
α |
|
С |
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
L |
||
стоящую от его середины С на рас- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
стоянии ℓ. При условии, что d и ℓ мно- |
S2 |
Рисунок 12 |
|
D′ |
||||||
|
|
|
||||||||
|
|
|||||||||
го меньше L, приближённо получим: |
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
d = Ll , откуда
По условию (6.5) в точке Р будет светлая полоса, если
|
= |
l |
d = ± mλ, |
|
(6.7) |
|
|
|
|
||||
|
|
|
L |
|
|
|
и по условию (6.6) в точке Р будет тёмная полоса, если |
|
|||||
= |
l |
d = ± (2m + 1) |
λ . |
(6.8) |
||
|
||||||
|
L |
2 |
|
|||
Отсюда, светлые полосы располагаются на расстояниях, считая от середины экрана С, равных
ℓ = ± m |
λ L, |
(6.9) |
|
d |
|
где m = 0, 1, 2, 3,... Тёмные полосы расположены между светлыми. Расстояние между соседними светлыми или соседними тёмными полосами (шири-
на интерференционной полосы) ℓ равно
41

Dℓ = |
λ L. |
(6.10) |
|
d |
|
Положение светлых полос можно определить также углом a = Ll (рису-
нок 12) по формуле (6.7):
a = m |
λ . |
(6.11) |
|
d |
|
Угловое расстояние между соседними светлыми (или тёмными) полосами равно:
Da = |
λ . |
(6.12) |
|
d |
|
Из равенства (6.12) видно, что угловое расстояние между полосами опре-
деляется отношением l/d, т.е. отношением длины волны l к расстоянию между источниками d. Это отношение l/d не должно быть мало, так как в противном случае интерференционные полосы расположатся на слишком малых угловых расстояниях друг от друга. Опыт показывает, что надо брать весьма близкие источники S1 и S2, чтобы полосы отстояли друг от друга на заметных угловых расстояниях. Так, Da = 10-3 (это соответствует расстоянию между полосами в 1 мм при L = 1 м), если отверстия S1 и S2 отстоят друг от друга на расстоянии d = 1 мм. Так из формулы (6.12)
l = Da×d, |
(6.13) |
то отсюда находим, что длина световых волн – величина очень малая, порядка
5×10-7 м.
При наблюдении в белом свете все полосы, кроме центральной, которой соответствует m = 0, окрашены, причём число наблюдаемых полос невелико. При наблюдении в свете какого-либо определённого цвета полосы имеют тот же цвет и могут быть насчитаны в значительно большем числе. При наблюде-
42
нии в красном свете полосы располагаются на больших угловых расстояниях
Δα друг от друга, а при наблюдении в синем свете – на меньших. Отсюда следует, что свет различного цвета отличается друг от друга длиной волны: красные лучи имеют большую, а синие меньшую длину волны. Белый свет представляет собою смесь волн различных длин, т.е. лучей различных цветов. Измерения дают, что лучам различных цветов соответствуют приблизительно приведённые в таблице 1 интервалы длин волн, выраженные в нанометрах.
Таблица 1
Цвет света |
Приблизительный интервал длин волн λ в нм |
|
|
Красный |
760 – 630 |
|
|
Оранжевый |
630 – 600 |
|
|
Жёлтый |
600 – 570 |
|
|
Зелёный |
570 – 500 |
|
|
Сине-зелёный |
500 – 450 |
|
|
Синий |
450 – 430 |
|
|
Фиолетовый |
430 – 400 |
|
|
Лучи с длинами волн больше 760 нм и меньше 400 нм человеческий глаз не воспринимает. Первые из них называются инфракрасными, вторые – ультрафиолетовыми. Свет какой-либо одной определённой длины волны называется монохроматическим.
При белом свете полосы различных цветов при больших m перекрываются и дают равномерное освещение. Этим объясняется, что в белом свете наблюдаемых интерференционных полос ограничено.
Важно отметить, что в опыте Юнга отверстия S1, S2 и S должны быть малы. Только при малых размерах отверстия S за ним возникает правильный волновой фронт, представляющий собою часть сферы, что обеспечивает одинаковость фаз колебаний в отверстиях S1 и S2 и, следовательно, определённую разность хода между волнами, сходящимися в любой точке экрана Р. При отсутствии постоянной разности фаз усиления волн не происходили бы всё время в од-
43

них и тех же местах и полосы размылись бы. При освещении экрана двумя независимыми источниками света в точках экрана не получится постоянных разностей хода, и интерференционные полосы не смогут возникнуть. Источники, колеблющиеся в одинаковых фазах или с постоянной разностью фаз, называются когерентными. Только когерентные источники дают определённым образом расположенные интерференционные полосы.
Два независимых источника света, например, две различные свечи или электрические лампочки, не когерентны. Каждый из них состоит из огромного числа атомов или молекул, являющихся независимыми элементарными излучателями. Между фазами, с которыми колеблются атомы обоих источников, нет никаких постоянных соотношений. Поэтому колебания, исходящие от всех атомов обоих источников, накладываясь друг на друга, дают в среднем равномерную освещённость. Тем не менее, можно осуществить различные схемы опытов, в которых искусственно создаются когерентные источники света от одного источника путём разделения света от одного источника на два пучка. Одну из таких схем – метод Юнга мы уже рассмотрели.
§ 1.7 Поляризация света
Описанные выше явления интерференции в одинаковой степени могут быть объяснены как допущением, что световые волны поперечны, так и допу-  щением, что они продольны. Однако существуют
щением, что они продольны. Однако существуют
|
|
|
|
|
|
|
|
В |
|
|
|
процессы, в которых проявляется различие между |
|
а |
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
поперечными и продольными волнами. В попереч- |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
а) |
А |
|
|
а′ |
||||||||
|
|
|
|
|
|
|
|
ной волне, распространяющейся в направлении аа′ |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(рисунок 13а), все точки вещества совершают коле- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
В |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
а |
|
|
|
|
|
|
|
|
|
бания в определённой плоскости АВ. Следовательно, |
||
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|||
|
б) |
|
|
А |
|
|
|
|
а′ поперечная волна по отношению к различным плос- |
||||
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
Рисунок 13 |
|
|
|
костям, проведённым через направление ее распро- |
|||
странения, обладает различными свойствами. В продольной волне колебания
44
совершаются вдоль направления распространения волны аа′, и ее свойства по отношению к любой плоскости АВ (рисунок 13б), проведённой через направление ее распространения, одинаковы.
Свет, испускаемый большинством источников света, например, раскалёнными твёрдыми телами, непосредственно не обнаруживает таких свойств, которые выявляли бы поперечный характер его колебаний. Поперечность свето-
вых колебаний удаётся обнаружить лишь |
|
|
|
А |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
после того, как свет испытает некоторые |
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
изменения, например отражение от грани- |
S |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
S′ |
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
α |
|
|
|
|
|
|
|
C |
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0′ |
||||
цы прозрачной среды. Пусть луч АВ (ри- |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
B |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
сунок 14) отражается в точке В от плоской |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
α |
|
|
|
|
|
а) |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
n′ |
|
|
|
|
|
D |
|||||
стеклянной поверхности S под углом α, а |
|
|
А |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
затем вторично отражается в точке С от |
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
S′ |
|
|
|||||||
другой плоской стеклянной поверхности S′ |
S |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
α |
|
|
|
|
|
|
С |
|
|
|
|
||||||
под тем же углом α. При поворачивании |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
B |
|
|
|
|
|
|
|
|
|
|
|
||||||||||
поверхности S′ около оси 00′, совпадаю- |
|
|
|
|
|
|
|
|
|
|
Рисунок 14 |
|
|
|
|
|
|
|
|
|
б) |
|||
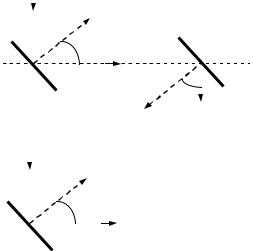
щей по направлению с падающим лучом ВС, угол падения α остаётся неизмен-
ным, а меняется лишь положение плоскости падения света на поверхность S′ по отношению к плоскости падения на поверхность S. Опыт показывает, что интенсивность луча CD зависит от относительного положения обеих плоскостей падения: луч CD имеет максимальную интенсивность, когда плоскости падения параллельны друг другу (рисунок 14а), и минимальную интенсивность, когда они взаимно перпендикулярны (рисунок 14б).
Таким образом, после первого отражения свет стал обнаруживать зависимость интенсивности отражённых лучей от ориентации плоскости падения. Свет, обладающий таким свойством, носит название поляризованного света.
При определённом значении угла α луч вовсе не отражается от второй пластинки, если плоскости падения на обе пластинки взаимно перпендикулярны. В этом случае свет называется полностью поляризованным. По закону, от-
45
крытому Брюстером, свет полностью поляризуется при угле падения α, удовлетворяющему условию:
tgα = n, |
(7.1) |
где n − показатель преломления вещества, от поверхности которого происходит отражение.
Условлено считать свет, отражённый от прозрачной поверхности под углом, удовлетворяющим закону Брюстера, поляризованным в плоскости падения. Введя такое понятие о плоскости поляризации, можно сказать: поляризованные лучи отражаются, когда плоскость поляризации перпендикулярна к плоскости падения.
Указанные факты легко истолковываются, если допустить поперечность световых волн. В световых волнах, испускаемых большинством источников света, колебания не упорядочены – они совершаются в различных плоскостях. Свет, представляющий собою такие колебания, называется естественным. В частично поляризованном свете колебания совершаются преимущественно в одной плоскости. В полностью поляризованном свете колебания совершаются только в одной определённой плоскости, как это изображено на рисунке 13а. Интенсивность, с которой отражаются волны от границы прозрачного вещества, зависит от того, какой угол составляет плоскость колебаний с плоскостью
падения. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
||
Поскольку само по себе неясно, при каком уг- |
|
А |
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
α |
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
α |
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
С |
|||||||
ле между плоскостями колебания и падения волны |
n1 |
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n2 |
|
|
|
|
|
|
|||||||||
отражаются с максимальной интенсивностью, по- |
|
В |
π/2 |
|||||||||||||
стольку неясно, совпадает ли плоскость колебаний с |
|
|
|
|
|
|
|
|
β |
|
D |
|||||
Рисунок 15 |
||||||||||||||||
условно введённой выше плоскостью поляризации |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
или нет. Этот вопрос может быть решён лишь на основании электромагнитной теории света, на что нами будет указано в § 1.8.
Формулируя закон Брюстера, мы считали, что свет падает на границу прозрачного вещества, граничащего с вакуумом, причём принимали во внима-
46
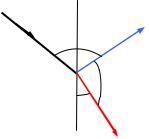
ние лишь отражённый луч. Рассмотрим теперь более подробно случай прохождения света через границу раздела двух веществ с показателями преломления n1 и n2. При падении луча АВ (рисунок 15) на границу раздела обоих веществ под углом α возникают два луча: отражённый луч ВС и преломлённый BD. Послед-
ний образует с нормалью угол β, удовлетворяющий закону преломления:
sinα = |
n2 |
sinβ. |
(7.2) |
|
n1 |
||||
|
|
|
Пусть падающий луч АВ является естественным, т.е. в нём присутствуют колебания любых направлений. Если угол падения удовлетворяет закону Брюстера, который теперь имеет вид:
tgα = |
n2 |
, |
(7.3) |
|
n1 |
||||
|
|
|
то преломлённый луч BD при этом частично поляризован в плоскости, перпендикулярной к плоскости падения. При естественном падающем луче преломлённый луч никогда не бывает полностью поляризован. Степень его поляриза-
ции максимальна при угле падения α, равном углу Брюстера. При выполнении закона Брюстера из формулы (7.3) имеем
sinα = |
n2 |
cosα. |
(7.4) |
|
n1 |
||||
|
|
|
Подставляя это значение sinα в формулу преломления (7.2), получим
cosα = sinβ. |
(7.5) |
Так как углы α и β оба острые, то из последнего равенства следует: 47
α + β = |
π |
, |
(7.6) |
|
2 |
|
|
откуда, в свою очередь, вытекает, что при падении света на границу двух прозрачных веществ под углом Брюстера отражённый и преломлённый лучи взаимно перпендикулярны.
§ 1.8 Электромагнитная природа света
Вопрос о природе света представляет собою одну из центральных проблем физической оптики. Исследования в этом направлении всегда лежали на магистральном пути развития науки. Многие крупные открытия в области физики, так или иначе, связаны с попытками глубже понять, что такое свет.
Кконцу XIX в. физика располагала набором фактов, свидетельствующих
впользу электромагнитной природы света. К их числу относятся опыты Фарадея, в которых наблюдалось влияние магнитного поля на распространение света в веществе, опыты Лебедева, в которых было измерено световое давление, опыты Герца, в которых было доказано существование электромагнитных волн, эксперименты по взаимодействию света с веществом.
Одним из первых аргументов в пользу электромагнитной природы света было совпадение скорости электромагнитных волн, вычисленной Максвеллом, со скоростью света. В 1849 г. Физо измерил скорость света и получил значение 315 000 км/с. В 1857 г. Вебер и Кольрауш измерили электродинамическую постоянную с, равную отношению электромагнитной и электростатической единиц заряда, и получили значение с = 310 800 км/с. В 1861 г. Максвелл вывел систему уравнений для электромкагнитного поля, из которой вытекала возможность существования электромагнитных волн, причём скорость распространения волны определялась значением электродинамической постоянной. Максвелл обратил внимание на то, что найденное Вебером и Кольраушем значение
48
с весьма близко к скорости света, измеренной Физо. Это позволило ему заключить, что свет представляет собой электромагнитную волну.
Опыты Герца. Предсказанное Максвеллом существование электромагнитных волн нуждалось в экспериментальной проверке. Эту задачу решил Герц, сумевший осуществить генерацию и приём электромагнитных волн и исследовавший их свойства.
Вэкспериментах с искровым разрядом мощной индукционной катушки Герцу удалось получить сверхбыстрые колебания электрического тока (период колебаний около 10-8 с). Продолжая опыты, Герц установил, что ток высокой частоты в прямолинейном отрезке проводника способен вызвать аналогичный ток в другом проводнике, удалённом от первого на некоторое расстояние. Так были открыты электромагнитные волны.
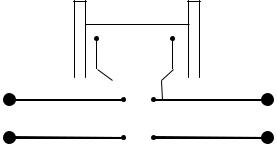
Водном из опытов Герц использовал собственные электрические колебания вибратора, состоящего из двух одинаковых металлических стержней, разделённых искровым промежутком (рисунок 16). С помощью
индукционной катушки К обе |
|
|
|
|
К |
|
|
Излучающий |
||
|
|
|
|
|
|
|
|
|
||
половины вибратора заряжались |
|
|
|
|
|
|
|
|
|
вибратор |
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
Р |
|
|
|
|
|
до высокого напряжения. Когда |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
М |
|
|
|
|||
разность потенциалов достигала |
|
|
|
|
|
|
Приёмный |
|||
|
|
|
|
|
|
|
|
|
||
пробойного значения, в разряд- |
|
|
|
|
|
|
|
|
|
|
Рисунок 16 |
|
|
|
|
|
вибратор |
||||
|
|
|
|
|
|
|
||||
нике Р проскакивала искра, замыкавшая обе половины вибратора, и в нём возникали затухающие электриче-
ские колебания высокой частоты. При этом вибратор испускал в пространство электромагнитную волну. Появление волны регистрировалось по возникновению искры в микрометре М приёмного вибратора.
Чтобы доказать единую сущность световых и электромагнитных волн, Герц попытался продемонстрировать отражение, преломление и поляризацию электромагнитных волн. Используя параболические зеркала из цинковой жести, Герц сумел сформировать пучок электромагнитных волн, подобный оптиче-
49
скому. При помощи изготовленной из твёрдой смолы призмы высотой 1,5 м и весом 1,2 т он добился отклонения пучка электромагнитных волн, соответствующего преломлению световых лучей в стеклянной призме. Наконец, он смог убедиться и в поляризации электромагнитных волн при помощи проволочной сетки. Подводя итог своим исследованиям, выполненным в 1886-1889 годах,
Герц написал: ²…мне представляется весьма вероятным, что описанные опыты доказывают идентичность света, тепловых лучей и электродинамического вол-
нового движения².
Таким образом, единая сущность света и электричества была подтверждена экспериментально. Оптика могла быть теперь включена в электродинамику так же, как акустика давно уже вошла в механику.
Шкала электромагнитных волн. Рисунок 17 показывает место оптического диапазона на шкале электромагнитных волн. Этот диапазон простирается от 0,4 до 0,7 мкм по длине волны и от 4×1014 до 7,5×1014 Гц по частоте.
Электромагнитные волны, возникающие около электрических вибраторов, и световые волны различаются лишь по длине. Электромагнитные волны имеют длину порядка метров, световые волны – порядка 5×10-5 см. Электромагнитные волны большой длины волны возникают при колебаниях электрических зарядов в макроскопических телах, световые волны – при колебаниях электронов внутри атомов и молекул.
Рентгеновские лучи испускаются твёрдыми телами при ударе о них потока быстрых электронов. Наиболее распространённым источником рентгеновского излучения является рентгеновская трубка, в которой сильно ускоренные электрическим полем электроны бомбардируют анод (металлическая мишень из тяжелых металлов, например, вольфрама или платины), испытывая на нём резкое торможение. При этом возникает рентгеновское излучение, представ-
ляющее собой электромагнитные волны с длиной волны примерно 10-10-10-6 см. При процессах, происходящих внутри атомных ядер, а также при тормо-
жении очень быстрых электронов испускаются так называемые g-лучи с длинами волн от 10-9 см и ниже.
50
