random books / Васильева - Рабочая тетрадь для лаб работ по физике. Ч. 2_ Электричество и магнетизм. Оптика и квантовая физика (2013)

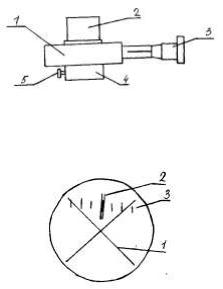
вставлен окулярный микрометр. Это дает возможность наблюдать кольца Ньютона в отраженном свете при нормальном падении световой волны на линзу, так как в оптической головке микроскопа установлены специальные призмы (призмы Шмидта), позволяющие направлять луч света на объект и от объекта под прямым углом, а окулярные трубки разворачивать по глазу наблюдателя.

На предметный столик микроскопа кладется приспособление, позволяющее получать интерференционную картину. Оно состоит из плотно прижатой выпуклой стороной плосковыпуклой линзы и плоскопараллельной пластинки.

Измерение радиусов колец Ньютона осуществляется с помощью окулярного микрометра (рис. 3).

Рис. 3 Окулярный микрометр состоит из корпуса 1 с хомутиком 4, который одевается на тубус

микроскопа и закрепляется винтом 5 окуляра 2 с диоптрийным механизмом. Вра щением окуляра устанавливают его на резкое изображение перекрестия 1 (рис. 4).

Рис. 4 В фокальной плоскости окуляра расположены неподвижная шкала 3 с делениями от 0 до 8 (рис. 4),

подвижные перекрестие 1 и индекс 2 в виде биштриха. При вращении микрометрического винта 3 (рис. 3) перекрестие 1 и биштрих 2 (рис. 4) перемещаются в поле зрения окуляра 2 относительно неподвижной шкалы 3. Шаг винта равен 1 мм. При повороте винта 3 за накатанную часть барабана (рис. 3) на один оборот биштрих и перекрестие в поле зрения окуляра (рис. 4) переместятся на одно деление шкалы.

Следовательно, неподвижная шкала в поле зрения служит для отсчета полных оборотов барабана винта.

Барабан 3 по окружности разделен на 100 частей. Поворот барабана на одно деление соответствует перемещению перекрестия на 0,01 делений неподвижной шкалы.

Полный отсчет по шкалам окулярного микрометра складывается из отсчета по неподвижной шкале и отсчета по барабану винта. Отсчет по неподвижной шкале в поле зрения определяется положением биштриха. Отсчет по барабану микрометрического винта производится как и по обычному микрометру, т. е. определяется деление шкалы, которое находится против индекса, нанесенного на неподвижном цилиндре барабана.

Измерение диаметра колец сводится к определению координат колец по шкале окулярного микрометра. Вращая барабан микрометрического винта, устанавливаем перекрестие на темное кольцо (вначале на правый край первого, затем второго, третьего и т. д., каждый раз производя отсчет по шкале и барабану, как сказано выше). Затем так же отсчитываем координаты ряда последовательных колец слева.

Вычитая из большей координаты меньшую для одного и того же кольца, получаем диаметр соответствующего кольца в условных единицах. Разделив диаметр на два, получаем значение радиуса. Умножив полученное значение радиуса кольца на переводной коэффициент, приведенный в таблице 1, получим истинный размер кольца в миллиметрах.

Порядок выполнения работы

1.Включите осветитель микроскопа.

2.На барабане увеличения микроскопа, где собраны призмы Шмидта, установите “2”.

21

3.Вращением окуляра за накатанную часть установите резкое изображение перекрестия в поле зрения окулярного микрометра.

4.Получите четкое изображение колец Ньютона в поле зрения окулярного микрометра.

5.Запишите в заранее подготовленную таблицу координаты 5 темных колец, считая от центрального темного пятна сначала справа, затем слева.

6.Найдите разность координат справа и слева для одного и того же кольца.

7.Определите истинный радиус колец, умножая на переводной коэффициент из таблицы 1

половину диаметра кольца, рассчитанного в пункте 6.

8.Зная длину волны зеленого цвета (мы пользуемся зеленым светофильтром λ=4,86∙10-7м) по уравнению (9) рассчитайте радиус кривизны линзы.

9.Все измерения занесите в таблицу 2.

Контрольные вопросы

1.Что такое интерференция света?

2.Каковы условия наблюдения интерференции света?

3.Чем отличаются интерференционные картины при наблюдении колец Ньютона в отраженном и

проходящем свете?

4.Почему при удалении от центра линзы, расстояние между кольцами Ньютона уменьшается?

5.Когда и почему кольца Ньютона оказываются окрашенными?

6.Где применяется явление интерференции?

7.Почему нельзя наблюдать интерференцию света в обычных условиях?

8.Что такое оптическая длина пути?

9.Напишите уравнение световой волны.

10.Какое свойство света проявляется в явлении интерференции?

11.Какие способы создания когерентных волн вы знаете?

22

Лабораторная работа №6 ИЗУЧЕНИЕ ЯВЛЕНИЯ ДИФРАКЦИИ И ОПРЕДЕЛЕНИЕ ДЛИНЫ ВОЛНЫ СВЕТА ПРИ

ПОМОЩИ ДИФРАКЦИОННОЙ РЕШЕТКИ

Цель работы: изучить явление дифракции; экспериментально определить границы видимой части спектра.

Приборы и принадлежности: оптическая скамья, дифракционные решетки, источник света, щелевая диафрагма, светофильтры и измерительная линейка.

Введение Дифракцией называется явление огибания волнами препятствий, встречающихся на их пути, или в

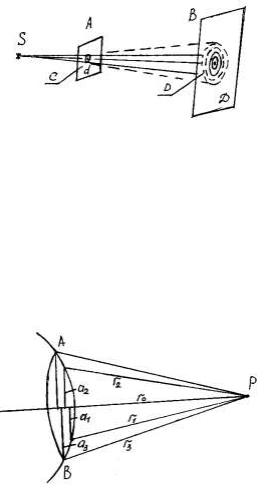
более широком смысле – любое отклонение распространения волн вблизи препятствий от законов геометрической оптики. Так, например, если свет от источника S (рис. 1) направить на непрозрачный экран А с круглым отверстием а, сравнимым с длиной волны λ, то на экране В вокруг светлого пятна наблюдаются размытые кольца в области геометрической тени, показанные пунктирными окружностями.

Дифракция объясняется на основе волновой теории света и принципа Гюйгенса. Часть поверхности волны, дошедшей до экрана А, проходит в отверстие а.

Рис. 1 Согласно принципу Гюйгенса каждая точка волновой поверхности излучает вторичные

элементарные волны, распространяющиеся от отверстия во всем полупространстве справа от экрана А. Дойдя до экрана В, они создают освещенность его за пределами светлого пятна, интенсивность которой убывает с удалением от него, причем неравномерно, образуя размытые светлые кольца. Образование этих колец обусловлено интерференцией света и объясняется с помощью зон Френеля.

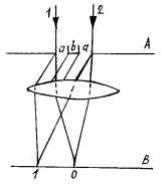
Метод зон Френеля лежит в основе изучения большинства дифракционных явлений и заключается в следующем. Пусть в точке S (рис. 2) помещен точечный источник света, а в точке Р находится наблюдатель. Фронт волны через некоторое время t займет положение АОВ и пересечет оптическую ось в точке C.

Рис. 2

Радиусом r0 из точки Р описываем сферическую поверхность, которая касается поверхности АОВ

описываем еще ряд сферических поверхностей, которые вырежут из поверхности АОВ ряд колец с радиусами а1, а2, а3... и т. д. Первое кольцо называется 1-й зоной Френеля, а 2-е, 3-е и т. д. зоны Френеля будут кольцами. Каждая зона излучает свет, а так как расстояния до соседних зон отличаются друг от друга на λ/2, то в точку Р от соседних зон будут приходить лучи с разностью хода λ/2, т. е. в противоположных фазах, а при равных амплитудах будут компенсировать друг друга. Но амплитуды лучей, пришедших в точку Р, будут тем меньше, чем больше номер зоны, т. е. чем дальше расположена зона от точки Р. В теоретическом курсе доказывается, что

23

результирующая амплитуда лучей Ар, пришедших от всех зон, если число зон стремится к бесконечности, оказывается равной половине амплитуды волны, пришедшей от 1-й зоны, или.

где АР — результирующая амплитуда колебаний в точке Р, А1 — амплитуда волны, пришедшей от 1-й зоны в точку Р.

Источник S из точки Р будет виден в направлении прямой РОS. Следовательно, явление дифракции не противоречит закону прямолинейного распространения света.

Применим рассмотренный метод зон Френеля для объяснения светлых колец, образующихся на экране В (рис. 1). Для этого из точки Р, расположенной в центре светлого пятна D на экране В необходимо описать ряд сферических поверхностей и посчитать, сколько зон Френеля укладывается на ширине отверстия “а”. Так как “а” мало, то на нем вмещается небольшое число зон. Будем считать амплитуды волн от различных зон, пришедших в точку Р, одинаковыми. Вследствие того, что расстояние до соседних зон отличается на λ/2, лучи в точку Р попадут с разностью хода λ/2 и при сложении полностью погасят друг друга. Отсюда вытекает правило: в точке наблюдения Р лучи будут усиливать друг друга, если на ширине отверстия укладывается нечетное число зон Френеля, и ослаблять — если четное число зон.

А так как число зон на ширине отверстия “а” зависит от положения точки наблюдения Р относительно точки S, то на экране будет наблюдаться либо усиление, либо ослабление интенсивности света. Весь экран покрывается чередующимися светлыми и темными кольцами ослабевающей интенсивности при удалении от центра пятна. В центре пятна Р тоже наблюдается чередование усиления и ослабления интенсивности вследствие, того, что при приближении экрана В к источнику S число зон, укладывающихся на ширине отверстия, увеличивается, а при удалении

— уменьшается.

Аналогичная дифракционная картина наблюдается также и в том случае, если вместо круглого отверстия диаметром “а”, в экране будет прорезана узкая щель шириной “а”. Кроме светлой полосы, расположенной в центре картины, ее называют максимумом нулевого порядка, представляющей собой изображение щели, получаются светлые полосы первого, второго и т. д. порядка, расположенные по обе стороны от полосы нулевого порядка ( рис. 3).

Чтобы рассмотреть образование этих полос, допустим, что в экране А прорезаны две щели шириной а, между которыми расположена непрозрачная полоса экрана шириной b (рис. 3). На щели падает плоская волна, ограниченная лучами 1 и 2. В теоретическом курсе доказывается, что указанные две щели можно рассматривать как два когерентных источника, каждый из которых создает свою дифракционную картину; наложение их друг на друга создает результирующую картину. Для ее наблюдения необходимо поставить линзу и сфокусировать лучи от обеих щелей на экране.

Рис. 3 Четкую дифракционную картину можно получить при использовании дифракционной решетки,

которая представляет собой прозрачную пластину с параллельными бороздками, прорезанными резцами специальной делительной машины. Бороздка отражает, рассеивает падающий на нее свет и выполняет роль темного промежутка между участками прозрачных поверхностей, которые хорошо пропускают свет и служат щелями решетки. В теоретическом курсе доказывается, что каждая из щелей решетки создает дифракционную картину. Эти картины накладываются друг на друга так, что на экране В максимумы каждой щели усиливаются, а минимумы ослабляются. В

24

результате образуется четкая дифракционная картина, состоящая из ярких узких полос, разделенных широкими темными полосами (рис. 4).

Рис. 4 Рис. 5 Рассмотрим пучок света, падающий на решетку перпендикулярно ее плоскости (рис. 5). Кроме

лучей, проходящих без отклонения, за решеткой будут лучи, отклоненные на различные углы. Выберем из всех отклоненных лучей только те лучи, которые отклонились на угол у от первоначального направления. До точки наблюдения эти лучи проходят разные пути, различающиеся на длину ВС. Если в этой разности хода укладывается четное число полуволн, то эти лучи усиливают друг друга, а если нечетное — то лучи ослабляют друг друга.

Отсюда следует записать простые соотношения для ВСД:

Если обозначить а + в = d, d называют постоянной решетки, то из уравнений (2) и (3) получаются условия главных максимумов и главных минимумов для решетки

Здесь знаки ± означают, что максимумы и минимумы располагаются по обе стороны от центрального (справа и слева).

Если решетку освещать белым светом, то максимумы будут окрашенными. Белый свет вследствие дифракции волн будет разлагаться в спектр. Причем, ближе к центральному (нулевому) максимуму будут расположены максимумы для фиолетовых лучей, а дальше от него — для зеленых, желтых, красных.

Уравнение (4) можно записать

Оно показывает, что угол дифракции лучей зависит от длины волны этих лучей. Число n называют порядком спектра. Чем больше n, тем слабее будет дифракционный максимум, n может принимать значения 0, 1, 2, 3...

В данной работе необходимо определить границы видимой части спектра, т. е. найти длины волн красного и фиолетового цветов. Из уравнения (4) получаем уравнение для определения длины волны света λ.

d — постоянная решетки. Она дается на приборе.

n— порядок спектра. Вы берете его сами. Лучше наблюдать первый порядок, т. е. ближайший за центральным.

Описание установки

25

Схема установки показана на рисунке. На оптической скамье 1 установили источник света S (электрическая лампа в кожухе с конденсором, позволяющим получать параллельный пучок лучей), непрозрачный экран 2 с узкой щелью и делениями и дифракционная решетка 3 .

Пучок лучей, пройдя через щель в экране 2 попадает на дифракционную решетку. Глядя на экран через дифракционную решетку, видим яркую белую щель, по обе стороны от которой располагаются спектры. Ближайший к щели спектр является первым, далее второй и т. д.

Порядок выполнения работы

1.Включите источник света.

2.Получите спектры при рассматривании щели на экране 2 через дифракционную решетку 3.

3.Измерьте расстояния от щели до экрана, от щели до красной и фиолетовой линий в спектрах первого порядка.

4.Данные занесите в заранее заготовленную таблицу.

5.Для каждого цвета по уравнению (10) определите длину волны.

6.Определите погрешности измерений.

Контрольные вопросы

1.Объясните явление дифракции света.

2.Сформулируйте принцип Гюйгенса—Френеля.

3.В каких условиях наблюдаются дифракционные явления?

4.В чем заключается метод зон Френеля?

5.Условия получения максимума дифракции от решетки и щели.

6.Что называется дифракционным спектром? Чем он отличается от призматического или дисперсионного?

7.Как и почему располагаются цветные линии в дифракционном спектре?

Лабораторная работа №7 ИЗУЧЕНИЕ ЗАКОНОВ ИЗЛУЧЕНИЯ АБСОЛЮТНО ЧЕРНОГО ТЕЛА И ИХ

ПРИМЕНЕНИЕ К НЕЧЕРНЫМ ТЕЛАМ

Цель работы: изучить законы излучения тел, устройство и работу пирометра и измерить коэффициент “нечерности” тел.

Приборы и принадлежности: пирометр с исчезающей нитью, проекционная лампа накаливания, автотрансформатор, амперметр, вольтметр.

26

Введение Все тела при любых условиях всегда излучают и поглощают энергию. Если температура тела

выше температуры окружающих тел, то оно излучает энергии больше, чем поглощает. Более холодные тела поглощают энергии больше, чем излучают. При равновесном состоянии вся энергия, поглощаемая телом, испускается им путем излучения, поэтому температура остается постоянной. Лучеиспускание происходит при любой температуре.

Спектры испускания нагретых тел являются сплошными, и они не могут характеризовать состав вещества. Спектры испускания нагретых тел зависят от температуры.

Кирхгоф ввел представление о теле, излучение которого не зависит от его физических и химических свойств и его состава, а зависит только от температуры, и всю падающую на него энергию оно поглощает. Такое тело назвали “абсолютно черным”. Такого тела в природе не существует, к нему приближается полость с поглощающими стенками и малым отверстием.

Все тела характеризуются лучеиспускательной и поглощательной способностями. Различают: лучеиспускательную способность тел или интегральную энергетическую светимость тел и спектральную энергетическую светимость или дифференциальную лучеиспускательную способность.

Лучеиспускательной способностью тел называют величину, численно равную всей энергии, испущенной всеми длинами волн с единицы площади тела в единицу времени, т. е.

где RT — лучеиспускательная способность тела или интегральная энергетическая светимость тела; W — энергия, излученная телом всеми длинами волн;

s — площадь излучения тела; t — время излучения.

Спектральной плотностью излучения называют энергию, испущенную с единицы площади тела в единицу времени в единичном интервале длин волн. Эта величина зависит не только от температуры тела, но и от интервала длин волн, которыми уносится энергия тела. Ее обозначают rλ,T . Эта величина связана с интегральной светимостью соотношением

Поглощательной способностью тел называют отношение энергии, поглощенной телом, ко всей падающей на это тело энергии.

Для реальных тел эта величина бывает меньше единицы. Для абсолютно черного тела она равна единице. Тела, не поглощающие энергию, называются “белыми”. Для них А = 0.

Кирхгоф установил закон, согласно которому отношение излучательной способности тела к его поглощательной способности для всех тел есть величина постоянная, зависящая только от температуры и не зависящая от химического состава тел. Этот закон справедлив как для интегральных величин, так и для дифференциальных.

rλ,T называют функцией Кирхгофа. Вид функции Кирхгофа был найден экспериментально и представлен на графике рис. 1 для разных температур. Здесь Т1<Т2<Т3.

Площадь под кривой характеризует интегральную излучательную способность тел. Стефан и Больцман установили, что интегральная излучательная способность абсолютно черного тела пропорциональна четвертой степени абсолютной температуры.

здесь σ — постоянная Стефана-Больцмана.

27

где А – коэффициент «нечерности» тела;

I - сила тока, прошедшего через исследуемое тело; U - напряжение на концах нагреваемого тела;

S - святящаяся площадь тела; TT - температура тела;

TC - температура среды;

σ - коэффициент Стефана-Больцмана.

Для чистых металлов А меняется от 0,15 до 0,3; для окислов – от 0,6 до 0,9.

Контрольные вопросы

1.Какие физические законы лежат в основе принципа действия пирометра?

2.Как читается закон Кирхгофа?

3.Что называется излучательной способностью тела?

4.Какова размерность излучательной способности тела в СИ?

5.Какой физический смысл имеет коэффициент, измеряемый в данной работе?

6.Что называется поглощательной способностью тела?

7.Какова единица измерения поглощательной способности тела в СИ?

8.Как читается закон Вина?

Лабораторная работа №8 ИЗУЧЕНИЕ ЛИНЕЙЧАТЫХ СПЕКТРОВ. ГРАДУИРОВКА СПЕКТРОСКОПА И

ОПРЕДЕЛЕНИЕ ПОСТОЯННОЙ РИДБЕРГА ПО СПЕКТРУ ГЕЛИЯ

Цель работы: ознакомьтесь с линейчатыми спектрами испускания водорода и гелия. Проградуируйте спектроскоп по спектру водорода. Определите постоянную Ридберга по спектру гелия.

Приборы и принадлежности: двухтрубный спектроскоп, газоразрядные трубки, заполненные водородом и гелием, высоковольтный генератор для поджига трубок, источник постоянного тока.

Введение Дисперсия света состоит в разложении белого света на его составляющие при пропускании белого света через трехгранную призму.

Явление дисперсии света объясняется зависимостью коэффициента преломления от длины световой волны.

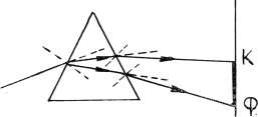
При пропускании белого солнечного света через трехгранную призму (рис. 1) на экране получают цветную полоску, называемую спектром.

Солнечный свет дает сплошной спектр с непрерывным переходом одних цветов в другие. Это означает, что в солнечном (белом) свете присутствуют электромагнитные волны всех длин волн.

Рис. .1 При использовании некоторых искусственных источников света спектр получается линейчатым.

Он состоит из отдельных светлых полос (линий), разделенных темными промежутками.

Это указывает на то, что свет от таких источников состоит лишь из колебаний, соответствующих определенным длинам волн. Линейчатый спектр дают разреженные газы при прохождении через них электрического тока, пары металлов при нормальном давлении. Установлено, что каждому элементу соответствует определенный спектр.

30