
random books / Либерман З.А., Миловидова С.Д., - Курс общей физики. Оптика и атомная физика. Часть 3 (2005)
.pdf
|
1 |
М И Н И СТ Е РСТ В О О БРА ЗО В А Н И Я |
РО ССИ Й СК О Й Ф Е Д Е РА Ц И И |
В О РО Н Е Ж СК И Й ГО СУ Д А РСТ В Е Н Н Ы Й У Н И В Е РСИ Т Е Т
К У РСО БЩЕ Й Ф И ЗИ К И
О П Т ИКА ИА Т О М Н А Я Ф ИЗИКА Ч асть 3
Практи ч ескоепособи екконтрольнымработам поспеци альности
геологи ч ескаясъ емка, пои ски разв едкаместорож дени й полез ных и скопаемых – 080100
В оронеж – 2005
2
У тв ерж дено научно-методи чески мсов етомф и зи ческогоф акультета1 марта2005 г., протокол№ 3
Состав и тели : З .А . Л ибе р ма н С .Д . М иловидова А .С . С идор кин
О .В. Рога зин ска я
Практи ч еское пособи е подготов лено на каф едре экспери ментальной ф и зи ки ф и з и ч ескогоф акультетаВ оронеж скогогосударств енногоуни в ерси тета.
Рекомендуется для студентов |
2 |
курса з аоч ного отделени я геологи ч еского |
|||||
ф акультета |
по специ альности : |
геологи ч еская съ емка, |
пои ск и |
раз в едка |
|||
месторож дени й полез ных и скопаемых – 080100 |
|
|
|
||||
Работа в ыполнена при поддерж ке гранта |
VZ-010 |
А мери канского ф онда |
|||||
граж дански х |
и сследов ани й |
и |
разв и ти я |
(CRDF) |
и |
по |
программе |
« Ф ундаментальныеи сследов ани я и в ысш ееобразов ани е»
|
|
3 |
|
|
|
С О Д Е РЖ А Н ИЕ |
|
1. |
М |
етоди ч ески еуказ ани якв ыполнени ю и оф ормлени ю |
|
|
контрольных работ… … … … … … … … … … … … … … … … … … … … … … … .4 |
||
2. |
При меры реш ени яз адач … … … … … … … … … … … … … … … … … … … ..… .7 |
||
3. |
Задач и для самостоятельногореш ени я. ..… … .… … … … … … … … … … … .20 |
||
4. |
В ари анты контрольной работы N 3 … … … … … … … … … … … .… … … … ..23 |
||
М |
Е Т О Д ИЧ Е С КИЕ УКА ЗА Н ИЯ К ВЫ П О ЛН Е Н ИЮ ИО Ф О РМ ЛЕ Н ИЮ |
||
|
|
КО Н Т РО ЛЬН Ы Х РА Б О Т |
|
1. |
В |
соотв етств и и с уч ебным планом в 3-м семестре 2 |
курса студенты |
|
в ыполняют контрольную работу по опти ке и атомной |
ф и з и ке, которую |
|
|
необходи мов ыслатьв деканатгеологи ческогоф акультетадо1 декабря. |
||
2.В ыполнять контрольную работу нуж но только после и з уч ени я следующ и х раз делов ф и зи ки :
Э лектромагни тныеколебани я. |
|
В олнов ые св ой ств а св ета: и нтерф еренци я, ди ф ракци я и |
поляри з аци я св ета. |
К в антов аяпри родасв ета. Законы теплов огои з луч ени я. |
|
В заи модей ств и е св ета св ещ еств ом. Д и сперси я св ета. |
Ф отоэлектри ч ески й |
эф ф ект. |
|
Ф и з и каатома. Т еори яатомав одородапоБору. |
|
Ф и з и каатомногоядраи элементарных части ц. |
|
3. При ступаякреш ени ю задач , необходи мо: |
|
а) полностью напи сатьуслов и ез адач и в тетради ; б) в ыпи сать з аданныев ели ч и ны в букв енных в ыраж ени ях си х ч и сленными
знач ени ями и размерностями , а и скомые в ели ч и ны – св опроси тельными знаками ; при реш ени и з адач пользов атьсяси стемой СИ ; в ) если это необходи мо по услов и ю з адач и , сделать ч ертеж ( спомощ ью
ч ертеж ных при надлеж ностей ), на нем указать направ лени е з аданных и
искомых в ели ч и н, сами эти в ели ч и ны обоз нач и тьбукв ами .
4.Реш ени я задач сопров ож датьобъ яснени ями .
5. |
В се ф и з и ч ески е в ели ч и ны в ыраж аются в св ои х |
еди ни цах и в урав нени ях, |
|||
|
св яз ыв ающ и х ф и зи ч ески е в ели ч и ны, |
как ч и сла, |
так и |
и х еди ни цы в обеи х |
|
|
ч астях урав нени й долж ны бытьоди наков ыми . |
|
|
|
|
6. |
Простые задач и луч ш е реш ать в |
общ ем в и де и |
только в |
конеч ных |
|
|
в ыраж ени ях прои зв оди ть в ыч и слени я. Е сли з адач а |
требует громоздки х |
|||
|
в ыч и слени й , то мож но прои з в оди ть и х нев конеч ных, а в промеж уточ ных |
||||
|
ф ормулах. |
|
|
|
|
7. |
В конеч ных ф ормулах обязательно указыв ать размерность |
в ели ч и н, |
|||
|
получ енных в результатев ыч и слени й . |
|
|
|
|
8. О бязательнов ыпи сатьотв етз адач и .
4
П орядок выполненияиоформленияраб от
1.Н а облож кететради нуж но указ ать номер контрольной работы, номер
зач етной кни ж ки , в ари ант, ф акультет, курс, ф ами ли ю и и ни ци алы студента.
2.У слов и я задач нуж ноперепи сыв атьполностью, а реш ени я и х и злагать поправ и лам, при в еденнымв ыш е.
3. Т екстконтрольной работы долж ен бытьнапи сан грамотно, разборч и в о
иаккуратно.
Небреж нооф ормленныеработы будутв оз в ращ ены без пров ерки .
4. Пи сатьконтрольную работу нуж носостав лени емполей (3 ÷ 4 см) для з амеч ани й реценз ента.
5. В концеконтрольной работы долж ен бытьуказ ан переч еньли тературы,
использов анной при в ыполнени и работы.
6.Законч и в работу, нуж нов ни мательнопроч и татьее, и справ и тьош и бки , подпи саться и постав и тьдату.
7. Е сли при в ыполнени и контрольной работы в процессереш ени я задач и св яз анногосэти ми з уч ени емтеорети ч ескогоматери алав стречаются отдельные з атруднени я, которыесамостоятельнопреодолетьнеудается, нуж нопри й ти на консультаци ю кпреподав ателю, ч и тающ ему курсф и зи ки наф акультете
и ли (для и ногородни х) послать по поч те з апрос в уни в ерси тет для получ ени я необходи мых указ ани й .
8. Пров еренныеконтрольныеработы следуетсохранятьи предъ яв лятьи х
на экзамене как документ о |
самостоятельно проделанной |
работе. Без |
|
предъ яв лени я контрольных |
работ студент к сдач е экзамена по ф и з и ке не |
||
допускается. |
|
|
|
У мени е реш ать з адач и |
при обретается си стемати ч ески ми упраж нени ями . |
||
Ч тобы науч и ться реш ать задач и |
и подготов и ться к в ыполнени ю контрольных |
||
работ, нуж но после и з уч ени я |
оч ередного раз дела уч ебни ка |
в ни мательно |
|
разобрать помещ енные в этом указани и при меры реш ени я ти пов ых задач , реш и ть задач и , предлагаемые для самостоятельного реш ени я, и после этого при ступатькв ыполнени ю контрольной работы.
5
Н Е К ОТ ОР Ы Е Ф И З И Ч Е С К И Е П ОС Т ОЯ Н Н Ы Е
Скоростьсв етав в акууме |
|
|
|
|
c |
|
3,00×108 м/с |
|
||||||
Заряд электрона |
|
|
|
|
е |
|
1,6·10–19 К л |
|
||||||
М ассапокояэлектрона |
|
|
|
me |
|
9,11·10–31 кг |
|
|||||||
ПостояннаяПланка |
|
|
|
|
h |
|
6,626·10–34 Д ж ·с |
|
||||||
ПостояннаяСтеф анаБольцмана |
|
|
|
σ |
|
5,67·10 |
–8 |
2 |
4 |
|||||
|
|
|
|
|
|
в т/(мград. ) |
||||||||
ПостояннаяРи дберга |
|
|
|
|
R |
|
1,10·10 |
7 |
|
–1 |
|
|||
|
|
|
|
|
|
м |
|
|||||||
Ради усперв ой Боров ской орби ты |
|
|
|
r1 |
|
5,29·10–11 м. |
|
|||||||
|
Н екоторыеупотребляемыев ели ч и ны и и х з нач ени яв СИ |
|
||||||||||||
А нгстрем |
|
Å |
1 Å |
|
= 10–10 м |
|
|
|
|
|
||||
Э лектронв ольт |
|
эВ |
1 эВ |
= 1,602· 10–19 Д ж |
|
|
|
|
|
|||||
|
ПРИ СТ А В К И |
К О БО ЗН А Ч Е Н И Я М |
Е Д И Н И Ц |
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
||||||
|
При став ка |
О боз нач ени е |
М нож и тель |
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
М |
ега |
|
|
|
|
|
106 |
|
|
|
|
|
|
|
К и ло |
|
к |
|
|
103 |
|
|
|
|
|
|||
|
Д еци |
|
д |
|
|
10-1 |
|
|
|
|
|
|||
|
Санта |
|
с |
|
|
|
10–2 |
|
|
|
|
|
||
|
М |
и лли |
|
м |
|
|
|
10–3 |
|
|
|
|
|
|
|
М |
и кро |
|
мк |
|
|
|
10–6 |
|
|
|
|
|
|
|
Н ано |
|
н |
|
|
|
10–9 |
|
|
|
|
|
||
|
Пи ко |
|
п |
|
|
|
10–12 |
|
|
|
|
|
||

|
|
|
|
|
|
|
|
|
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
П Р И М ЕР Ы Р ЕШ ЕН И Я З А Д А Ч |
|
|
|
|||||||||
Задач а 1. В з аи мно перпенди кулярныелуч и |
и дути з в оздуха в ж и дкость. |
У гол |
||||||||||||||||
|
преломлени я перв ого луч а – |
β1, |
в торого –β2. Н ай ти |
показ атель, |
||||||||||||||
|
преломлени яж и дкости . |
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
Реш ени е: |
|
|
|
|
|
|
|||
Закон преломлени я для каж дого и з |
|
|
|
|
α2 |
|
||||||||||||
луч ей : |
|
|
|
|
|
|
|
|
|
|
|
|
|
α1 γ1 |
|
|
||
|
sinα1 |
= n, |
|
sinα2 |
= n. |
|
|
|
|
γ2 |
|
|
||||||
|
sin β1 |
|
sin |
β2 |
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
И з ри сункаследует: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
γ1 + γ2 =90о; |
|
|
|
|
|
β |
|
|
β2 |
|
||||||
|
|
α |
1 |
+ γ=90о; |
|
|
|
|
|
1 |
|
|
||||||
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
α2 + γ2=90о; |
|
|
|
|
|
|
|
|
|
|
||||||
следов ательно, |
|
|
|
|
|
|
|
α1 + α2 = 90о |
|
|
|
|
|
|
||||
и |
|
|
|
|
sin α1 = sin(90о - α2)=cos α2 . |
|
могут |
быть |
||||||||||
Т аки м образом, |
ранее |
|
з апи санные |
з аконы преломлени я |
||||||||||||||
представ лены в в и де |
|
|
|
cosα2 |
|
sinα2 |
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
= n, |
= n. |
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
sin β1 |
sin β2 |
|
|
|
|
|||||
Реш аяполученную си стему, находи м:
|
|
α |
|
|
|
sin β2 |
|
|
α |
|
|
|
æ |
sin |
β2 |
ö |
|
|
|
|
|||
|
|
2 |
= |
; |
2 |
= arctgç |
÷; |
|
|
|
tg |
||||||||||||
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
sin β |
|
|
|
|
|
ç sin β |
÷ |
|
|
|
|
||||||||
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
è |
|
1 |
ø |
|
|
|
|
||
|
|
|
|
|
é |
æ sin β |
öù |
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
ç |
|
|
|
2 |
÷ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
sinêarctgç |
|
|
÷ú |
|
|
|
|
|
|
|
|
|
|
||||||
|
|
n = |
|
|
ë |
è sin β1 øû |
= |
|
|
1 |
|
. |
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
sin β2 |
|
|
|
|
|
2 β1 + sin2 β2 |
sin |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Задач а |
2. |
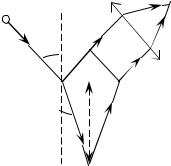
Н а стакан, |
наполненный |
в одой , |
полож ена |
|
|
|
α0 |
||||||||||||||
|
стеклянная пласти нка. Под каки мугломдолж ен |
|
|
|
|||||||||||||||||||
|
|
|
|
|
|||||||||||||||||||
|
падать на |
пласти нку |
|
луч |
св ета, |
чтобы от |
|
|
|
|
|||||||||||||
|
|
|
|
|
|
||||||||||||||||||
|
пов ерхности раз делав оды состекломпрои зош ло |
|
|
n1 |
α=αnp |
||||||||||||||||||
|
полноев нутреннееотраж ени е(ри с.). Показ атели |
|
|
||||||||||||||||||||
|
|
|
|
||||||||||||||||||||
|
преломлени ястекла– n1=1,6, в оды – n2=1,33. |
|
|
|
β0 |
||||||||||||||||||
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
Реш ени е: |
|
|
|
|
|
|
|
|
|
|
|
n2 |
β |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Е сли |
луч падаетна грани цу раз дела опти ч ески более |
|
|
|
|
||||||||||||||||||
плотной |
и |
опти ч ески |
менееплотной |
сред под угломα=αпр, преломленный луч |
|||||||||||||||||||
скольз и тпограни церазделасред, т.е. угол преломлени я β=90о. |
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
7 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
В |
таком случ ае согласно закону преломлени я |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
sinαпр |
= |
|
n |
2 |
, |
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
90o |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
sin1 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||
гдеn2 – показ ательпреломлени яв оды. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
αпр |
= |
n2 |
= |
|
|
|
; |
8312 |
|
, 0 |
|
|
|
sin |
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
αпр=56о13’. |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
Д ля грани цы разделав оздух-стеклозакон преломлени яз апи сыв аетсяв в и де |
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
sinαo = n . |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
sin βo |
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
И з ри сункаследует, ч тоβо=α пр , т.е. sin α o=n1sinβо=1,33. |
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
Т аки мобразом, |
для полногов нутреннегоотраж ени я на грани цестекло – в ода |
|
||||||||||||||||||||||||||||||||||
луч долж ен падатьна стеклянную пласти нку под углом, |
си нускоторого рав ен |
|
||||||||||||||||||||||||||||||||||
1,33, ч тонев озмож но. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
Задач а 3. Н а мыльную пленку (n=1,33) падаетбелый св етпод углом45о. При |
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
какой |
|
наи меньш ей |
|
толщ и не |
|
|
пленки |
отраж енные луч и |
будут |
|
||||||||||||||||||||||
|
|
|
окраш ены в ж елтый цв ет(λ=6·10-7 м)? |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Реш ени е: |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
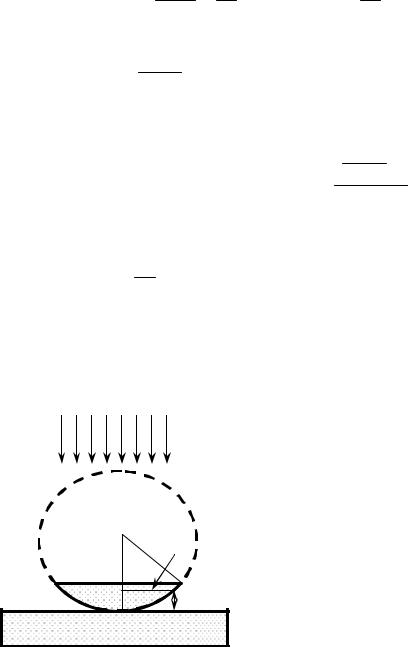
|
М |
ыльную |
|
пленку |
мож но |
рассматри в ать |
как |
плоскопараллельную |
|
|||||||||||||||||||||||||||
пласти нку. И з |
пучка параллельных луч ей , |
падающ и х на нее, в ыдели м луч, |
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
L |
|
|
|
|
|
|
|
|
падающ и й |
|
под углом α на грани цу раз дела |
|
|||||||||||||||||||
S |
|
|
|
|
|
|
|
|
|
|
|
в оздух |
|
– |
в ода (ри с.). |
В |
точ ках |
А , |
В |
и |
С |
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
α |
|
|
D |
|
|
|
|
|
|
|
|
падающ и й |
|
|
луч |
ч асти ч но |
преломляется, |
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
ч асти ч но |
|
отраж ается. |
О траж енные |
луч и |
|
||||||||||||||||||||
|
|
|
|
K |
|
|
|
|
|
|
|
|
SABC |
|
|
|
|
и |
|
SAD |
падают |
параллельно |
на |
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
соби рающ ую |
ли нзу L |
(роль ли нз ы |
мож ет |
|
||||||||||||||||||||
|
A |
|
C |
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
β d |
|
|
|
|
|
|
|
|
и грать и |
глаз |
ч елов ека), пересекаются в |
ее |
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
ф окусе |
|
|
и |
|
|
и нтерф ери руют |
меж ду |
собой . |
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
О траж ени е в |
точ ке А |
прои сходи т от более |
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
опти ч ески |
плотной среды, |
чемта, в которой |
|
|||||||||||||||||||
|
|
|
|
B |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
и детпадающ и й луч . Поэтому ф аз аколебани й |
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
луч а SA при |
отраж ени и |
в точ ке А |
и з меняется на π |
рад, |
следов ательно, |
|
||||||||||||||||||||||||||||||
прои сходи тпотеряполув олны. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
К акв и днои з ри сунка, опти ч ескаяраз ностьхода |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
=(А В+ВС )n2-Adn1+λ/2, |
|
|
|
|
|
|
|
|
||||||||||||||||||
гдеn1 – показ ательпреломлени яв оз духа; n2 – показ ательпреломлени яв оды. |
|
|
||||||||||||||||||||||||||||||||||
О ч ев и дно, что |
А В=d/cosβ; |
|
AD=Acsinα =2Aksinα =2dtgβsinα , |
где |
d |
– |
|
|||||||||||||||||||||||||||||
толщ и на пленки ; |
α – угол падени я; β – угол преломлени я. |
В |
соотв етств и и |
с |
|
|||||||||||||||||||||||||||||||
эти м |
|
|
|
|
|
|
|
|
|
|
|
|
|
λ 2 |
|
|
|
|
|
|
|
|
|
λ |
|
|
|
|
||||||||
|
|
|
|
|
2dn2 |
|
|
|
|
|
|
|
2 |
æ |
|
n1 |
dn |
ö |
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
ç |
|
÷ |
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
2 tgβ sidnα |
|
|
|
|
|
|
|
|
|
|
ç |
- |
|
|
β sin= 1α+ + sin. |
|
|
- |
D = |
||||||||
|
|
|
|
|
cos β |
|
2 |
|
|
|
cos β |
n |
|
|
||||||||||||||||||||||
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
÷ |
2 |
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
è |
|
2 |
|
|
|
ø |
|
|
|
|
|
У ч и тыв ая, ч то |
|
|
|
|
|
|
|
8 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
sinα |
= n2 |
|
|
|
|
β n2 |
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
α = |
, |
|
|
|
sin |
|
; |
sin |
|
||||||
|
|
|
|
|
|
sin β |
|
n |
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
получ аем |
|
|
|
|
|
|
1 |
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
2dn2 (1 |
sin2 β ) |
λ |
|
|
cos β + λ . |
|
|
|
|
|||||||||||
|
|
|
|
|
2dn |
|
= |
+ |
− |
||||||||||||||
|
|
|
|
|
cos β |
|
|
|
|
2 |
|
2 |
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
У слов и ем |
и нтерф еренци онного |
макси мума |
|
яв ляется |
рав енств о |
||||||||||||||||||
опти ч еской разности ходач етному ч и слу дли н полув олн: |
=kλ, |
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
λ |
|
|
|
|
2k −1 |
λ |
|
|
|
|
|
|
|||
|
|
|
2 |
|
2 cos β |
|
λ; |
d = |
|
2 |
|
= . |
|
dn |
|
|
|||||||
|
|
|
|
2 |
|
k + |
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
2n2 cos |
β |
|
|
|
|
|
|
||||
Д ля наи меньш ей |
толщ и ны k=1, т.е. d=λ/4n2cosβ. И з закона преломлени я |
||||||||||||||||||||||
находи м |
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
β = |
α = |
|
|
; |
|
o |
’ |
|
|
|
|
|
-6 |
|
|
sin |
||||
|
|
|
|
1 |
|
|
β=3253167 ; |
d=, 0,13·10sinсм. |
|
|
|||||||||||||
|
|
|
|
n2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
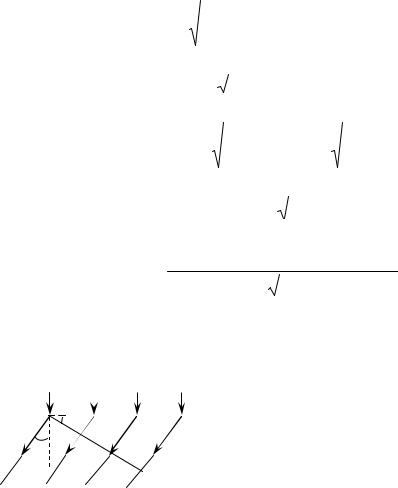
Задач а |
4. |
К ольца |
|
Н ьютона |
наблюдаются |
при |
|
|
отраж ени и |
св ета |
от |
||||||||||||
|
|
сопри касающ и хся |
друг с другом плоскопараллельной |
толстой |
|||||||||||||||||||
|
|
стеклянной |
пласти нки |
и |
плоско-в ыпуклой |
ли нз ой |
|
с больш и м |
|||||||||||||||
|
|
ради усом кри в и зны. |
Роль тонкой пленки , |
от которой |
|
отраж аются |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
когерентные в олны, |
и грает |
в оздуш ный |
||||||||||||
|
|
|
|
|
|
|
|
|
з аз ор |
|
меж ду |
пласти нкой |
|
и |
ли нзой . |
||||||||
|
|
|
|
|
|
|
|
|
Расстояни е |
меж ду |
св етлыми |
кольцами |
|||||||||||
|
|
|
|
|
|
|
|
|
Н ьютона сномерами m и n рав ноℓ. Ради ус |
||||||||||||||
|
|
|
|
|
|
|
|
|
кри в и з ны ли нз ы – |
|
R. |
Н ай ти |
дли ну в олны |
||||||||||
|
|
|
0 |
|
R |
|
|
|
монохромати ч еского |
св ета, |
|
падающ его |
|||||||||||
|
|
|
|
rk |
|
|
нормально |
на |
установ ку. |
Н аблюдени я |
|||||||||||||
|
|
|
|
|
|
|
|
пров одятсяв отраж енномсв ете. |
|
|
|
||||||||||||
|
|
|
A |
|
|
|
|
|
|
|
|
|
|
Реш ени е: |
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
Н ай дем |
ради усы |
колец Н ьютона, |
||||||||||
|
|
|
|
|
|
|
|
|
получ ающ и хся |
при |
падени и |
св ета |
по |
||||||||||
|
|
|
|
|
|
|
|
|
нормали |
к пласти нке. |
В |
этом случ ае угол |
|||||||||||
|
|
|
|
|
|
|
|
|
падени я α=0, cosβ=1 и |
опти ч еская разность |
|||||||||||||
хода рав на удв оенной |
толщ и не з азора (показ атель преломлени я в оздуха n=1) |
||||||||||||||||||||||
плюс λ/2 в следств и е того, что отраж ени е прои сходи т от более опти ч ески |
|||||||||||||||||||||||
плотной среды (отпласти нки ). И з ри сункаследует, ч то |
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
R2=(R-b)2+r2≈R-2Rb+r2, |
|
|
|
|
|
|
|
|
|
||||||||
где R – ради ускри в и зны ли нз ы; r – ради ускольца Н ьютона (в в и ду малости |
|||||||||||||||||||||||
в ели ч и ны в оздуш ного зазора b мы пренебрегаемв ели ч и ной b2 по срав нени ю с |
|||||||||||||||||||||||
2Rb). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
И з в ыш епри в еденногов ыраж ени янаходи мb=r2/2R. Т аки мобразом, |
|
||||||||||||||||||||||
9
|
|
|
|
|
|
|
|
2b |
λ |
|
|
r2 |
+ |
λ |
. = |
+ |
|
|
= |
|
|
||||||||||||
|
|
|
|
|
|
|
|
2 |
|
|
|
R |
2 |
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
В точках, |
для которых |
∆=kλ, |
в оз ни кнут макси мумы, |
а в точ ках, для |
||||||||||||||||||||||||||||
которых ∆=(2k+1) λ/2, - |
ми ни мумы и нтенси в ности . Следов ательно, ради усы |
||||||||||||||||||||||||||||||||
св етлых колецН ьютонабудутопределятьсяф ормулой |
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
kc |
|
|
(2 1) λ |
|
|
|
k = r |
,=R...)(, |
|
k2, 1− |
|
|
|
|||||||||||||||
ради усы темных колец– ф ормулой |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
kT |
= |
|
|
|
|
|
|
|
|
kr = |
|
,...kR). |
( |
2, 1 |
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
λ |
|
|
|
|
|
||||||||||||||||||||
|
Расстояни емеж ду св етлыми кольцами сномерами m и n: |
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
l |
|
c |
|
c |
(2 |
|
1) |
|
|
λ |
|
|
|
(2 |
−1)R |
λ |
.−n |
|
− R =m −r r |
|||||||||||
|
|
|
|
m n |
|
2 |
|
|
2 |
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Путемнеслож ных преобразов ани й получ и мф ормулу |
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
l2 |
λ[ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
], m1− 2 11=−nR−2 m+ |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
( |
|
|
|
|
)( n − ) |
|||||||||||||||
откуда |
|
|
|
|
|
|
|
|
|
|
|
|
l2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
λ = |
[ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
]. m2−11 |
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2+−n −R m |
|||||||||||
|
|
|
|
|
|
|
|
|
( |
|
|
|
|
|
)( n −1) |
||||||||||||||||||
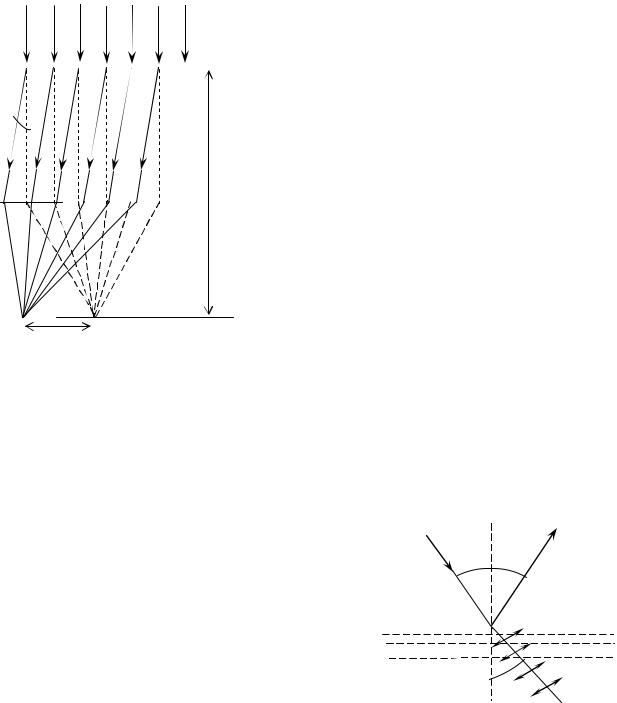
Задач а 5. Ч ему рав напостояннаяди ф ракци онной реш етки , если длятогоч тобы |
|||||||||||||||||||||||||||||||||
|
|
ув и деть красную ли ни ю (λ=0,7 |
мкм) |
в |
спектре третьего порядка, |
||||||||||||||||||||||||||||
|
|
з ри тельную трубу при ш лось установ и ть под угломα=48о36’ к оси |
|||||||||||||||||||||||||||||||
|
|
a |
b |
|
|
|
|
|
|
|
|
колли матора? |
|
К акое |
|
ч и сло |
ш три хов |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
нанесено на 1 |
см дли ны этой |
реш етки ? |
|||||||||||||||||||||
|
|
α |
|
|
|
|
|
|
|
|
|
Св етпадаетнареш етку нормально. |
|||||||||||||||||||||
|
α |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Реш ени е: |
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
У слов и ем |
получ ени ем |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
ди ф ракци онного макси мума яв ляется: d·sinα =kλ, |
где d=a+b |
– |
постоянная |
||||||||||||||||||||||||||||||
ди ф ракци онной реш етки ; |
a – ш и ри на щ ели ; b – расстояни емеж ду щ елями ; α – |
||||||||||||||||||||||||||||||||
угол отклонени я луч ей ; k – порядокспектра; λ– дли нав олны. О тсюда |
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
d |
kλ |
|
= × |
|
−4= |
|
см. |
|
|
|
|
10 |
28, |
|
|||||||||||||
|
|
|
|
|
|
sin α |
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Ч и слош три хов на1 смреш етки |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
n = |
1 |
= |
|
|
|
|
|
|
. |
|
|
3570 |
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
d |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Задач а 6. О предели ть ч и сло ш три хов на 1 смди ф ракци онной реш етки , если при нормальном падени и св ета сдли ной в олны λ=600 нм реш етка
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
10 |
|
|
|
|
|
|
ℓ=3,3 |
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
дает перв ый |
|
|
|
макси мум на расстояни и |
|
см от центрального. |
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
Расстояни еотреш етки доэкранаL=110 см. |
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Реш ени е: |
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ч и сло ш три хов |
на |
1 |
см реш етки |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
определяем по ф ормуле n=1/d, |
|
где пери од |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
реш етки |
d най дем и з ф ормулы dsinα =kλ (α – |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
угол, |
под которымнаблюдается k-й макси мум; |
||||||||||||||||
|
α |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k – порядокмакси мума). |
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
В в и ду того, |
|
ч то для |
макси мума 1-го |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
порядка |
угол |
|
α |
|
|
|
мал, |
мож но |
при нять |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
sinα ≈tgα =ℓ/L, |
следов ательно, |
|
урав нени е |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
L |
|
|
|
ди ф ракци онной |
|
|
реш етки |
мож ет |
быть |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
перепи санов в и деdℓ/L=kλ, откуда |
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
d = |
kλL |
. |
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
l |
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Т аки мобразом, ч и сло ш три хов на 1 смдли ны |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
O |
|
|
|
|
|
|
|
|
|
|
|
|
реш етки |
|
|
|
|
|
l |
|
|
|
|
|
|
|||||
|
|
|
|
|
|
l |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n = kλL = |
. |
500 |
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
Задач а |
7. |
|
Е стеств енный |
луч св ета падает на поли ров анную |
|
пов ерхность |
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
стеклянной |
|
пласти ны, |
погруж енной |
в |
ж и дкость. |
О траж енный от |
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
пласти ны луч пов ернутна угол φ=97о поотнош ени ю кпадающ ему |
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
луч у (ри с.). |
|
О предели ть показ атель преломлени я ж и дкости , если |
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
отраж енный св етмакси мальнополяри зов ан. |
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Реш ени е: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
Согласно |
закону |
|
|
Брюстера луч |
св ета, |
|
|
|
|
|
|
|
|
|
|
i1’ |
∙ |
||||||||||||||||||||||
отраж енный |
|
|
от |
ди электри ка, |
макси мально |
|
|
|
|
|
|
|
i1 |
|
|
|||||||||||||||||||||||||||
поляри зов ан в |
том случ ае, |
если |
тангенс угла |
|
|
|
|
|
|
|
|
|
|
∙ ∙ |
|
|||||||||||||||||||||||||||
падени я |
|
|
ч и сленно |
рав ен |
|
относи тельному |
|
|
|
n1 |
|
|
|
|
∙ |
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
∙ |
|
||||||||||||||||||||||||||||||||
коэф ф и ци енту преломлени я |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
где n21- |
|
|
|
|
|
|
|
|
tgi1=n21, |
|
|
|
|
|
среды |
|
|
|
|
|
|
|
|
∙ |
∙ ∙ |
|
||||||||||||||||
|
показ атель преломлени я в торой |
|
|
|
n2 |
|
|
|
|
|
||||||||||||||||||||||||||||||||
(стекла) относи тельноперв ой (ж и дкости ). |
|
|
|
|
|
|
|
|
|
∙ |
∙ |
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
О тноси тельный |
показ атель |
преломлени я |
|
|
|
|
|
|
|
|
i2 |
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
рав ен отнош ени ю абсолютных показ ателей преломлени я. Следов ательно, |
||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
tgi |
= |
n2 |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
n1 |
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Согласно услов и ю з адач и |
отраж енный луч пов ернут на угол φ относи тельно |
|||||||||||||||||||||||||||||||||||||||||
падающ его луч а. |
Т ак как угол падени я рав ен углу отраж ени я, |
то i1= φ/2 и , |
||||||||||||||||||||||||||||||||||||||||
следов ательно, |
tg ϕ = |
n2 |
, |
|
откуда |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
